Федеральное агентство по образованию
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ЭКОНОМИКИ И УПРАВЛЕНИЯ – «НИНХ»
по выполнению индивидуальных домашних заданий по дисциплине
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ
Для студентов очной формы обучения всех специальностей
Новосибирск 2005
Методические указания рассмотрены и утверждены на заседании кафедры экономико-математических методов и прогнозирования от 6 июня 2005 г., протокол № 7.
1. Задача 1. Задача о производстве автомобилей. . . . . . . . . . . . . . . . . . . . . . . . 4
2. Задача 2. Задача об оптимальной оптовой закупке товаров. . . . . . . . . . . . 10
3. Задача 3. Задача о выборе оптимального плана производства продукции . 15
4. Литература. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
Задача 1. Задача о производстве автомобилей
Фирма по производству автомобилей выпускает модели типа А и В. Годовые производственные мощности цехов приведены в следующей таблице:
|
№ |
Название цеха |
Количество машин за год |
|
|
типа А |
типа В |
||
|
1 |
Кузовной |
660 |
440 |
|
2 |
Шасси |
1200 |
400 |
|
3 |
Моторный |
560 |
560 |
|
4 |
Сборочный |
990 |
495 |
Требуется:
1. Составить экономико-математическую модель расчёта оптимальной годовой
программы выпуска автомобилей с целью получения максимальной прибыли от их реализации.
2. Определить наиболее прибыльную для фирмы производственную программу,
если расчётная прибыль от одной машины типа А составляет 8712,1 рублей, а
прибыль от одной машины типа В составляет 19318,2 рублей.
3. Указать, насколько изменится максимум суммарной прибыли фирмы, если
предположить, что годовая производительность цеха «шасси» окажется:
а) сниженной на 20%,
б) увеличенной на 10%.
Решение:
1. Пусть х1 – планируемое количество выпускаемых за год машин типа А,
х2 – планируемое количество выпускаемых за год машин типа В.
На выпуск всех машин двух типов каждому цеху дается период времени 1 год, причем все цеха работают одновременно.
На примере кузовного цеха представим расчет затрат времени на изготовление одного автомобиля каждого типа.
В
цехе за 1 год выпускается 660 автомашин типа А, тогда на производство одной
машины потребуются затраты времени равные ![]() от
годового объема времени.
от
годового объема времени.
В
этом же цехе за 1 год также выпускается 440 машин типа В, значит на производство
одной машины потребуются затраты времени равные ![]() от
годового объема времени. Таким образом:
от
годового объема времени. Таким образом:
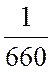 – норма расхода
времени на производство одного автомобиля типа А в кузовном цехе (величина
выражена в долях года);
– норма расхода
времени на производство одного автомобиля типа А в кузовном цехе (величина
выражена в долях года);
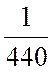 – норма расхода
времени на производство одного автомобиля типа B в кузовном цехе
(в долях года).
– норма расхода
времени на производство одного автомобиля типа B в кузовном цехе
(в долях года).
Аналогично рассчитываются временные затраты на производство одного автомобиля каждого типа для других цехов.
Покажем формирование ограничений по ресурсу «время» на примере того же кузовного цеха.
Время работы цеха (в долях года) по изготовлению общего количества выпускаемых автомобилей типов А и В можно представить следующим образом:
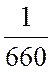 х1 +
х1 + 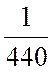 х2 .
х2 .
Так как временной ресурс фирмы на выпуск всех машин составляет 1 год, значит время работы цеха не должно превышать объема времени в 1 год. Отсюда получим ограничение:
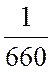 х1
+
х1
+ 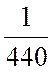 х2
х2 ![]() 1.
1.
Рассуждая подобным образом, получим ограничения по ресурсу «время» для других цехов.
Ограничения, которым должны удовлетворять значения
переменных х1 и х2, связаны с тем, что эти переменные
обозначают количество выпускаемых машин. Поскольку количество машин не может
быть величиной отрицательной, то значения х1 и х2 должны
быть неотрицательны, т.е. х1![]() 0, х2
0, х2![]() 0.
0.
Обозначим прибыль, получаемую фирмой, через Z. Величину прибыли необходимо максимизировать. Учитывая расчетную прибыль от одной машины каждого типа, суммарная прибыль фирмы от продажи всех произведенных автомобилей примет вид:
Z =
8712,1х1 + 19318,2х2![]() max.
max.
Экономико-математическая модель расчета оптимальной годовой программы выпуска автомобилей:
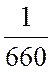 х1 +
х1 + 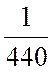 х2
х2 ![]() 1,
1,
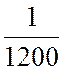 х1 +
х1 + 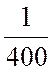 х2
х2 ![]() 1,
1,
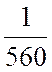 х1 +
х1 + 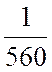 х2
х2 ![]() 1,
1,
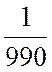 х1 +
х1 + 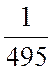 х2
х2 ![]() 1,
1,
х1![]() 0, х2
0, х2![]() 0,
0,
Z = 8712,1х1 + 19318,2х2![]() max.
max.
Для удобства расчетов приведем систему ограничений к следующему виду:
2х1 + 3х2 ![]() 1320,
1320,
х1 + 3х2 ![]() 1200,
1200,
х1 + х2 ![]() 560,
560,
х1 + 2х2 ![]() 990,
990,
х1 ![]() 0, х2
0, х2 ![]() 0,
0,
Z =
8712,1х1 + 19318,2х2![]() max.
max.
2. Решим задачу графическим методом.
Напомним основные этапы графического способа решения ЗЛП.
1. Строят граничные прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.
2. Находят полуплоскости, определяемые каждым из неравенств задачи.
3. Находят область допустимых решений (ОДР).
4.
Строят вектор-градиент целевой
функции ![]() = (с1;с2),
компоненты которого равны коэффициентам при переменных целевой функции.
Значения компонент можно пропорционально изменять.
= (с1;с2),
компоненты которого равны коэффициентам при переменных целевой функции.
Значения компонент можно пропорционально изменять.
5. Строят прямую с1 х1 + с2 х2 = h, которая называется линией уровня целевой функции. Здесь h может быть любым числом. Все линии уровня параллельны между собой и перпендикулярны вектору-градиенту.
6. Передвигают линию уровня по направлению, указанному вектором-градиентом. Последняя точка соприкосновения линии уровня и ОДР является точкой, в которой целевая функция принимает максимальное значение.
7. Определяют координаты точки максимума функции и рассчитывают значение целевой функции в этой точке.
Выпишем уравнения граничных прямых и по две точки на этих прямых для ограничений задачи.
2х1 + 3х2 = 1320 (1.1) х1 + 3х2 = 1200 (1.2)
![]()
![]()
![]()
![]() х1 0
660 х1
0 1200
х1 0
660 х1
0 1200
![]()
![]() х2 440 0 х2
400 0
х2 440 0 х2
400 0
х1 + х2 = 560 (1.3) х1 + 2х2 = 990 (1.4)
![]()
![]()
![]()
![]() х1 0
560 х1 0
990
х1 0
560 х1 0
990
![]()
![]() х2
560 0 х2
495
0
х2
560 0 х2
495
0
![]() х2
х2

![]()
 560
560
![]()
![]()
![]() 495
495
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.