![]()

![]()
![]() 440
440
400 А


 |
![]()

![]() х1
х1
![]()
![]() Z = 0 560 660
990 1200
Z = 0 560 660
990 1200
![]()
![]() (1.4) (1.2)
(1.4) (1.2)
(1.3) (1.1)
Рисунок 1. Графическое решение задачи о производстве автомобилей.
На рисунке 1 представлено решение задачи определения оптимальной годовой программы выпуска автомобилей.
Областью допустимых решений является пятиугольник, образованный осями координат и прямыми (1.2), (1.1), (1.3).
Вектор-градиент ![]() = (87; 193). Строим линию уровня
вида: 8712,1х1 + 19318,2х2
= 0.
= (87; 193). Строим линию уровня
вида: 8712,1х1 + 19318,2х2
= 0.
Точка максимума А находится на пересечении первой и второй прямых.
Найдем ее координаты, решив систему уравнений:
![]() 2х1 + 3х2 = 1320,
2х1 + 3х2 = 1320,
х1 + 3х2 = 1200.
Решением системы будет вектор X * = (120; 360).
Оптимальная программа выпуска
автомобилей: 120 машин типа А и 360 машин
типа В за год.
Суммарная прибыль для этого выпуска автомобилей составит:
Z = 8712,1 ![]() 120 + 19318,2
120 + 19318,2 ![]() 360
= 8000004 (руб.).
360
= 8000004 (руб.).
3. Исследуем изменения прибыли с изменением производительности цеха «шасси».
а) Если производительность цеха «шасси» снизится на 20% ,
т.е. станет составлять 80% от исходной производительности, то норма расхода
времени по цеху «шасси» на производство автомобиля типа А будет равна 1200 ![]() 0,8 = 960, а для автомобиля типа В –
400
0,8 = 960, а для автомобиля типа В –
400 ![]() 0,8 = 320.
0,8 = 320.
Второе ограничение примет следующий вид:
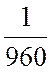 х1 +
х1 + 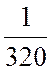 х2
х2 ![]() 1,
1,
или
х1 + 3х2 ![]() 960.
960.
Вместо прямой (1.2) появится прямая (1.2`): х1 + 3х2 = 960.
Координаты точек для построения граничной прямой (1.2`):
![]()
![]() х
х![]() 1 0
960
1 0
960
х2 320 0
График, отражающий снижение производительности цеха «шасси» на 20% (остальные ограничения остаются без изменения), представлен на рисунке 2.
Относительно исходной прямой (1.2) прямая (1.2`) сместится ближе к началу координат.
ОДР на рисунке 2 теперь представляет четырехугольник, образованный осями координат и прямыми (1.2`) и (1.3).
Точкой максимума будет точка А` на пересечении прямых (1.2`) и (1.3):
![]() х1 + 3х2 = 960,
х1 + 3х2 = 960,
х1 + х2 = 560.
Решением этой системы является вектор X * = (360; 200).
![]() х2
х2
![]() 560
560
 0
0
![]()
![]()
495
![]() 440
440
![]()

![]()
![]()
![]()
![]() 320
320
![]()
![]()


![]() А`
А`
![]()
![]() а
560 660 960
990 х1
а
560 660 960
990 х1
![]()
![]() Z = 0
Z = 0
![]() (1.1) (1.4)
(1.1) (1.4)
(1.3) (1.2`)
Рисунок 2. Графическое решение при снижении производительности цеха «шасси».
Вывод:
при снижении производительности цеха «шасси» на 20 % оптимальный
производственный план выпуска автомобилей составит 360 машин типа А и
200 машин типа В в год.
Суммарная прибыль при новом условии составит:
Z` = 8712,1 ![]() 360 + 19318,2
360 + 19318,2 ![]() 200 = 6999996 (руб.).
200 = 6999996 (руб.).
Очевидно, исходная прибыль Z уменьшилась на величину:
∆Z = Z – Z` = 8000004 – 6999996 = 1000008 (руб.).
б) Если производительность цеха «шасси» увеличится на 10% , т.е. станет 110% от исходной производительности, то второе ограничение модели преобразуется следующим образом:
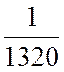 х1 +
х1 + 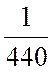 х2
х2 ![]() 1,
1,
или
х1 + 3х2 ![]() 1320.
1320.
Вместо прямой (1.2) появится прямая (1.2"): х1 + 3х2 = 1320.
Координаты точек для построения граничной прямой (1.2"):
![]()
![]() х
х![]() 1 0
1320
1 0
1320
х2 440 0
В данном случае ОДР представляет четырехугольник, образованный осями координат и прямыми (1.3) и (1.1).
Точкой максимума целевой функции будет точка А″, образованная пересечением прямых (1.1), (1.2`) с осью ординат OX2. Ее координаты найдем, решив систему уравнений:
![]() х1 + 3х2 = 1320,
х1 + 3х2 = 1320,
х1 = 0.
Решение системы: X * = (0; 440).
Вывод: при увеличении производительности цеха «шасси» на 10 % в оптимальный план выпуска автомобилей входит выпуск только машин типа В в количестве 440 штук.
Суммарная
прибыль при этом будет равна Z" = 19318,2 ![]() 440
= 8500008 (руб.).
440
= 8500008 (руб.).
![]()
х2
 |
560

495 ![]()
![]()
![]()
![]()
![]()
 А″
А″
 |
![]() х1
х1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.