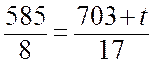Графический метод и двойственность: Методические указания по выполнению индивидуальных домашних заданий по дисциплине "Экономико-математические модели", страница 7

, откуда найдем значение t = 540,125.

  Определим верхнюю границу интервала изменения трудоресурсов:

703 + 540,125 = 1243,125.

  Итак, при увеличении объема трудоресурсов до 1243,125 чел.-час. сохраняется выпуск продукции вида 1 и вида 3, которые включены в оптимальный план.

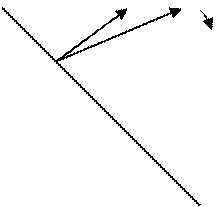
Пусть количество используемых трудоресурсов уменьшается, т.е. t < 0.

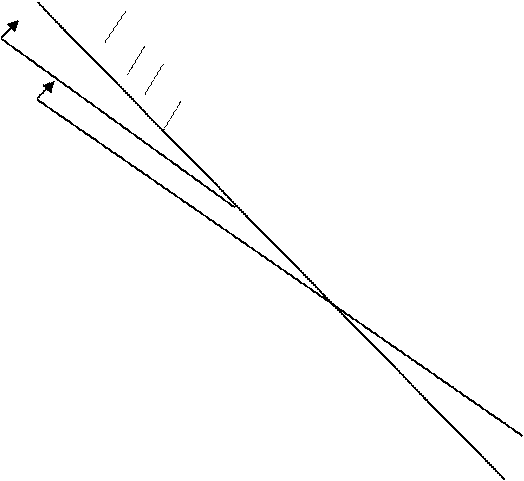
  Рассуждения аналогичны вышеизложенному. Различие в том, что если уменьшать значения параметра t, вектор-градиент будет поворачиваться по часовой стрелке и «прижимается» к оси u₁ (рисунок 6). При некотором определенном значении t линия уровня целевой функции 585u₁ + (703 + t)u₂ = 0, которая тоже поворачивается по часовой стрелке, станет параллельна прямой (3.3).

  Это будет предельной ситуацией, когда точка А остается точкой минимума. Если продолжить уменьшение значений t, произойдет смена точки А на новую точку минимума В (7,4; 48,2) на пересечение прямых (3.4) и (3.3).                    

По признаку параллельности прямых коэффициенты линии уровня                       585u₁ + (703 + t)u₂ = 0 и прямой (3.3) пропорциональны:

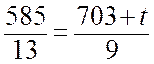, откуда t = – 298.

Определим нижнюю границу интервала изменения трудоресурсов:

703 – 298 = 405.

  При уменьшении объема трудоресурсов до 405 чел.-час. обязательно сохранится выпуск видов продукции: продукта вида 1 и продукта вида 3, которые включены в оптимальный план.

  Таким образом, диапазон изменения трудовых ресурсов, при котором сохраняется оптимальный план выпуска продукции, определяется интервалом [405; 1243,125].  

  Другими словами, если рассмотреть задачу выбора оптимального плана производства продукции, в которой вместо значения 703 чел.-час. в правой части второго ограничения будет стоять любое значение из интервала [405; 1243,125], то оптимальное решение будет включать выпуск продукции вида 1 и вида 3, а оптимальное решение соответствующей двойственной задачи будет оставаться неизменным:

u= 20 руб./кг, u= 30 руб./чел.-час.

                   u₂

 

               Л       С

 

                                       В                 

 

                                                А

                 

 

                 

 

                   7,03                                                                                  D

                                                                                                                             u₁

                          5,85                                                                  (3.2)                                      

                                          W = 0                                                          (3.1)

                                                                                                  (3.3)

(3.4)

Рисунок 6. Графическое решение двойственной задачи при уменьшении трудоресурсов.

  Однако следует отметить, что объемы оптимального выпуска продукции вида 1 и вида 3 зависят от объема используемого трудоресурса (при неизменном объеме    сырья). Рассмотрим пример. Пусть объем трудоресурсов равен 1001 чел.-час. Это значение входит в найденный диапазон изменения трудоресурсов.

  Формируется новая задача выбора оптимального плана производства продукции:

8х₁ + 9х₂ + 13х₃ + 16х₄  585,

17х₁ + 15х₂ + 9х₃ + 8х₄  1001,

х_j  0,      j = ,

Z = 670х₁ + 504х₂ + 530х₃ + 504х₄  max.

  Поскольку значения двойственных оценок остаются неизменными, то анализ по первому условию дополняющей нежесткости (#) дает те же выводы: х₁  0, х₂  = 0,   х₃  0, х₄  = 0.

  Анализ по второму условию дополняющей нежесткости приводит к следующей  системе уравнений (с учетом х₂ = х₄ = 0):

8х₁ + 9х₂ + 13х₃ + 16х₄ = 585,

17х₁ + 15х₂ + 9х₃ + 8х₄ = 1001.

  Находим оптимальный план выпуска продукции:  X ^* = (52; 0; 13; 0).

  5. Изменения объема используемого трудоресурса в найденном интервале воздействуют на выручку фирмы.

  Рассчитаем изменение выручки при росте трудоресурсов на d₁ = 180 чел.-час.

  Новый объем использованных трудоресурсов 703 + 180 = 883 чел.-час. находится в пределах рассчитанного диапазона изменения трудоресурсов, 883 ∈ [405; 1243,125].

Рост выручки составит:

∆Z = d₁ u₂  = 180 чел.-час.  30 руб./чел.-час = 5400 руб.

  Рассчитаем изменение выручки при убыли трудоресурсов на d₂ = 99 чел.-час.

  Новый объем использованных трудоресурсов 703 – 99 = 604 чел.-час. находится в пределах рассчитанного диапазона изменения трудоресурсов, 604 ∈ [405; 1243,125].

Уменьшение выручки составит:

∆Z = d₂ u₂ = 99 чел.-час.  30 руб./чел.-час. = 2970 руб.

  Итак, при увеличении или уменьшении объема трудоресурсов в рассчитанном диапазоне [405; 1243,125] выручка фирмы будет увеличиваться или уменьшаться на величину ∆Z.

ЛИТЕРАТУРА

1.   Барабаш С.Б.,  Воронович Н.В. Экономико-математические методы. Учебное пособие. Новосибирск, 2004.

2.  Акулич И.Л. Математическое программирование в примерах и задачах. – М.:Высшая школа, 1986.

3.  Бахтин А.Е., Высоцкий Л.Л., Савиных В.Н. Сборник задач по математическому программированию. – Новосибирск: НГАЭиУ, 1994.

4.  Исследование операций в экономике, под редакцией Н.Ш.Кремера – М.: Банки и биржи, 1997.

5.  Экономико-математические методы и прикладные модели, под редакцией В.В. Федосеева – М.:ЮНИТИ, 2000.

6.  Бахтин А.Е. Математическое моделирование в экономике.– Новосибирск, НГАЭиУ, 1998.

7.  Эддоус М., Стэнсфилд Р. Методы принятия решения. –М.: ЮНИТИ, 1997.

Графический метод и двойственность

Методические указания

к выполнению индивидуальных домашних заданий

Подписано к печати                                2005г.

НГУЭУ, ул. Каменская, 56.