Графический метод и двойственность: Методические указания по выполнению индивидуальных домашних заданий по дисциплине "Экономико-математические модели", страница 6

     Вторая группа условий:                                         

    u₁(585 – 8х₁ – 9х₂ – 13х₃ – 16х₄) = 0,

    u₂(703 – 17х₁ – 15х₂ – 9х₃ – 8х₄) = 0.

   Проведем анализ первой группы условий:

х₁(8u₁+17u₂ – 670) = 0, подставим рассчитанные ранее значения u₁^* = 20, u₂^*= 30 в выражение, стоящее в скобках,  8  20 + 17  30 – 670 = 0.

Поскольку значение в скобках равно нулю, а произведение должно быть равно нулю по условию дополняющей нежесткости, следовательно, другой множитель х₁  0.

Аналогичны следующие рассуждения:

  х₁(8u₁ + 17u₂ – 670) = 0, 

       8  20 + 17  30 – 670 = 0              х₁ 0,

  х₂(9u₁ + 15u₂ – 504) = 0,                   

     9  20 + 15  30 – 504 0             х₂ = 0,

  х₃(13u₁ + 9u₂ – 530) = 0,                   

     13  20 + 9  30 – 530 = 0            х₃  0,

  х₄(16u₁ + 8u₂ – 504) = 0,                   

     16  20 + 8  30 – 504 0            х₄ = 0.

Проведем анализ по второму условию дополняющей нежесткости:

u₁(585 – 8х₁ – 9х₂ – 13х₃ – 16х₄) = 0, но поскольку множитель u₁ = 20, а произведение должно быть равным нулю, следовательно, выражение в скобках будет равно нулю, т.е. 585 – 8х₁ – 9х₂ – 13х₃ – 16х₄ = 0, или 8х₁ + 9х₂ + 13х₃ + 16х₄ = 585.

  Рассуждая аналогично, получаем:

u₁(585 – 8х₁ – 9х₂ – 13х₃ – 16х₄) = 0,

u₁ = 20  8х₁ + 9х₂ + 13х₃ + 16х₄ = 585,

u₂(703 – 17х₁ – 15х₂ – 9х₃ – 8х₄) = 0,

u₂ = 30  17х₁ + 15х₂ + 9х₃ + 8х₄ = 703.

  В результате подстановки в условия дополняющей нежесткости оптимальных значений u₁^*, u₂^* получена система уравнений относительно неизвестных величин х₁, х₂, х₃, х₄, решение которой позволит получить оптимальные значения х₁^*, х₂^*, х₃^*, х₄^*.

Выпишем полученную систему уравнений:

  8х₁  +  9х₂ + 13х₃ + 16х₄  = 585,

17х₁ + 15х₂ +  9х₃ +  8х₄  = 703,

               х₂                       = 0,

                                     х₄ = 0.

Решая данную систему, находим оптимальные значения переменных х₁^* = 26,         х₂^* = 0, х₃^* = 29, х₄^* = 0.

  Вычислим значение целевой функции:

Z = 670  26 + 504  0 + 530  29 + 504  0 = 32790,    Z = W.

  На основании положений теории двойственности найден оптимальный план производства продукции  X ^* = (26; 0; 29; 0).

4.Условия, для которых составлялась исходная модель задачи, могут меняться в реальных условиях работы.

  Предлагается рассмотреть ситуации, когда объем используемого трудоресурса может увеличиваться или уменьшаться, однако найденный план выпуска продукции при этом не должен измениться.

  Это значит, что виды выпускаемой продукции останутся те же (продукт 1 и продукт 3), т.е. должны сохраниться значения х₁ > 0, х₃ > 0, х₂ = х₄ = 0, полученные из условий (#). Для этого должно остаться неизменным оптимальное решение двойственной задачи, т. е. u₁^* = 20, u₂^* = 30.

  Введем параметр t, означающий изменение количества использованных трудоресурсов. Значение t = 0 соответствует первоначальному объему трудоресурсов 703 чел.-час.

  С появлением параметра t экономико-математическая модель исходной задачи примет вид:

8х₁ + 9х₂ + 13х₃ + 16х₄  585,

17х₁ + 15х₂ + 9х₃ + 8х₄  703 + t,

х_j  0,      j = ,

Z = 670х₁ + 504х₂ + 530х₃ + 504х₄  max.

Двойственная задача:

                                                          8u₁ + 17u₂  670,

                  9u₁ + 15u₂  504,

13u₁ +   9u₂  530,

16u₁ +   8u₂  504,

u₁  0,     u₂   0,

W = 585u₁ + (703 + t)u₂ min.

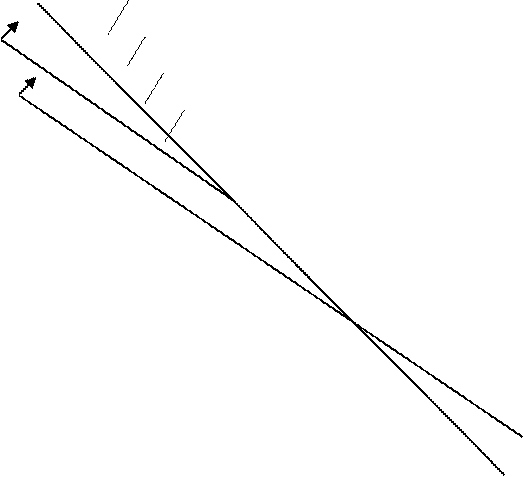
  Найдем диапазон изменения параметра t, при котором оптимальное решение двойственной задачи сохраняется.

Пусть количество используемых трудоресурсов увеличивается, т.е. t > 0.

  Если увеличивать параметр t, вектор-градиент  будет поворачиваться против часовой стрелки и «прижиматься» к оси u₂ (рисунок 5), т.к. коэффициент при u₁ остается постоянным, а коэффициент при u₂ возрастает с увеличением параметра t.

  Линия уровня функции W с ростом параметра t тоже поворачивается против часовой стрелки. Незначительные перемещения её обычно не приводят к изменению оптимальной точки (для нашей задачи точки А, в которой пересекаются прямые (3.1) и (3.3)).

  Предельной ситуацией, когда точка А остается еще точкой минимума, является ситуация, при которой линия уровня становится параллельной прямой (3.1). Пока точка А является оптимальной, будут сохраняться значения u₁ = 20,  u₂ = 30.

                   u₂

 

                Д      С

 

                                       В                 

 

                                                А

                 

 

                 

 

                    7,03                                                                                 D

                                                                                                                             u₁ 

                          5,85                                                                  (3.2)                                     

                                                                                                        (3.1)

                                    W = 0                                                    (3.3)

                                                                            (3.4)

Рисунок 5. Графическое решение двойственной задачи при увеличении трудоресурсов.

  Однако в результате более значительных изменений угла наклона линии уровня появится новая оптимальная точка. Для нашей задачи ею станет точка D (83,7; 0) на пересечении прямой (3.1) и прямой u₂ = 0.

  Определим промежуток значений параметра t, для которых точка А является оптимальной.

  Рассмотрим линию уровня вида: 585u₁ + (703 + t)u₂ = 0.

  Предельным положением линии уровня (т.е. моментом, когда произойдет смена решения) будет положение, когда она станет параллельна прямой (3.1), т.е. уравнению  8u₁ + 17u₂ = 670.

  По признаку параллельности прямых коэффициенты в уравнении линии уровня и прямой (3.1) станут пропорциональными, т.е.