Министерство образования Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ЭКОНОМИКИ И УПРАВЛЕНИЯ
Матричные игры
Методические указания
к выполнению индивидуальных домашних заданий
по «Экономико-математическим методам»
Для студентов очной формы обучения всех специальностей
Новосибирск 2005
Методические указания рассмотрены и утверждены на заседании кафедры экономико-математических методов и прогнозирования « » 2005г., протокол №___
Составитель: к. ф.-м. н., доцент М. В. Пудова
СОДЕРЖАНИЕ
Текст заданий ………………………………………………………………..5
Элементы теории игр ……………………………………………………….6
Методические указания ……………………………………………………10
Задача 1.Графическое решение матричных игр....................................10
Задача 2. Об оптовой закупке при неопределенности розничной
продажи. ………………………………………………………14
Задача 3.Задача о структуре посевов. ………………………………..17
Литература ……………………………………………………........................21
Предлагаемые методические указания предназначены для оказания помощи студентам очной формы обучения при изучении курса «Экономико-математические методы» и выполнения индивидуальных домашних заданий по теме «Матричные игры». Содержат полный текст заданий, необходимый теоретический минимум и методические указания по решению предложенных задач.
Текст заданий
Задача 1. Графическое решение матричных игр.
Дана матричная игра с платежной матрицей:
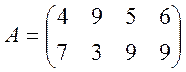 .
.
Используяграфический анализ игры, найти оптимальные смешанные стратегии игроков и цену этой матричной игры.
Рассмотреть матричную игру с платежной матрицей, являющейся транспонированной к предложенной матрице. Решить эту игру графически и сравнить полученные результаты.
Задача 2. Об оптовой закупке при неопределенности розничной продажи.
Торговая фирма на каждый предстоящий день решает вопрос об объемах оптовой закупки скоропортящихся продуктов двух наименований.
По статистике наблюдений за местным рынком этих товаров при холодной и дождливой погоде на каждые 2 ед. товара А в среднем реализуется 3 ед. товара В, а при жаркой солнечной погоде товары реализуются в усредненной пропорции 5 ед. товара А к 1 ед. товара В.
Оптовая цена товара А равна 4 руб., а оптовая цена товара В − 3 руб. Розничная цена товара А составляет 7 руб., а товара В − 6 руб.
Товары, закупленные по оптовым ценам в расчете на холодную погоду с учетом известной пропорции на сумму 9775 руб., полностью удовлетворяют спрос на эти товары при холодной погоде. Аналогичное замечание верно для солнечной погоды.
Ежедневные издержки на розничную реализацию продукции составляют 1900 руб.
Остающийся в конце дня нереализованный товар фирма сдает на пищевую переработку по ценам на 75 % меньше оптовой.
Администрацию интересует, в каких объемах следует сделать оптовые закупки этих товаров, чтобы максимизировать гарантированную в среднем прибыль фирмы в условиях полной неопределенности предстоящей погоды.
Требуется:
1. Составить игровую математическую модель предложенной ситуации, рассчитав соответствующую платежную матрицу.
2. Указать оптимальную стратегию закупок фирмы, наиболее неблагоприятную для фирмы погоду и гарантированный максимум прибыли фирмы, найдя решение полученной матричной игры.
3. Какова будет ожидаемая прибыль фирмы при выборе рассчитанной оптимальной стратегии, если учесть информацию, что вероятность завтрашнего дождя равна 40 %? Какова будет новая оптимальная стратегия и новая ожидаемая прибыль фирмы при учете этой информации?
Задача 3. Задача о структуре посевов.
Агрофирма может выращивать любую из культур А и В. Требуется установить, какими из этих культур и в каких пропорциях нужно засеять земли, принадлежащие фирме, чтобы в предстоящем сезоне после продажи урожая получить максимальную гарантированную в среднем выручку с одного гектара используемых земель.
Достоверный прогноз погоды отсутствует, и неизвестно, будет ли предстоящее лето засушливым, дождливым или нормальным. Средняя урожайность этих культур в зависимости от погоды, установленная на основе прошлого опыта, приведена в следующей таблице (в ц/га):
|
Засушливое лето |
Нормальное лето |
Дождливое лето |
|
|
Культура А |
18 |
22 |
32 |
|
Культура В |
17 |
9 |
7 |
Считая агрофирму первым игроком, имеющим две чистые стратегии: засеять всю площадь культурой А или культурой В, а природу − вторым игроком, имеющим три чистых стратегии: установить засушливое, нормальное или дождливое лето, составить матрицу выигрыша первого игрока. При этом учесть, что цены на продажу 1 ц культуры А и культуры В в следующем году прогнозируются на уровне 1 тыс. руб. и 2 тыс. руб. соответственно.
Найти и пояснить оптимальную смешанную стратегию посевов агрофирмы, наиболее неблагоприятную для агрофирмы смешанную стратегию природы и цену полученной матричной игры.
Элементы теории игр
Предметом теории игр являются ситуации, в которых важную роль играют конфликты и совместные действия. В отличие от линейного программирования в теории игр рассматриваются ситуации, в которых решения принимают несколько действующих лиц.
Ситуация называется конфликтной, если в ней участвуют стороны, интересы которых полностью или частично противоположны. Классическим примером конфликта является ситуация, в которой есть один продавец и один покупатель. Другой пример конфликтной ситуации − это существование на рынке нескольких производителей одного и того же товара, обладающих достаточной силой для воздействия на цену этого товара (ситуация олигополии). Конфликт может проявиться не только в результате сознательных действий различных участников, но и как результат действия «стихийных сил». Подобные ситуации называют «играми с природой». Вторая и третья задачи из индивидуального задания являются «играми с природой».
Лица, принимающие участие в рассматриваемом конфликте, называются игроками. Игроки могут различаться по своим именам (например, Продавец и Покупатель) или по номерам в случае конечного числа игроков (например, 1-й и 2-й игрок при игре в «орлянку»).
Любая игра ведется по определенным правилам. Правилами игры называются допустимые действия игроков, направленные на достижение ими некоторой цели. В соответствии с этими правилами игроки предпринимают некоторые действия, делают ходы. Однозначное описание действий игрока в каждой из возможных ситуаций, в которой он должен сделать личный ход, называется стратегией игрока.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.