Матричные игры: Методические указания к выполнению индивидуальных домашних заданий по курсу "Экономико-математические методы", страница 4

Выпишем соотношения для нахождения  оптимальной смешанной стратегии первого игрока, основываясь на утверждении 3. В нашем примере платежная функция, согласно (7),  имеет вид:

  

Пусть оптимальная смешанная стратегия первого игрока равна . По утверждению 3 он получит выигрыш,  равный цене игры , с какими бы вероятностями не применял второй игрок свои активные стратегии. Мы рассмотрим случаи, когда второй игрок применяет свои активные чистые стратегии, т.е. либо первую, либо вторую.

Итак, пусть , . Тогда .

Пусть , . Тогда . Приравняем эти значения к цене игры  и добавим уравнение , получим систему уравнений:

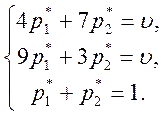                                                       (9)

Решив эту систему, получаем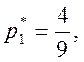   

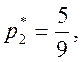
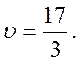
Теперь найдем оптимальную смешанную стратегию второго игрока. Пусть она задается вектором . Здесь мы учли тот факт, что третья и четвертая чистые стратегии второго игрока являются пассивными. Выпишем величину проигрыша второго игрока, если он применяет свою оптимальную смешанную стратегию, а первый игрок − свои чистые стратегии.

Пусть  . Тогда .

Пусть  . Тогда .

Применяем утверждение 3, учитывая, что цена игры найдена и равна 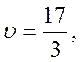 получим систему уравнений:

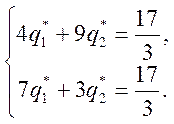
Решив эту систему, получаем 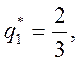 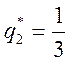. Итак, оптимальная смешанная стратегия второго игрока задается вектором .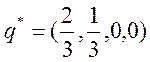

Ответ к данной задаче запишем в виде:

, .

                                                                                                                        

2. Рассмотрим теперь матричную игру, платежная матрица которой является транспонированной к матрице задачи 1, т.е. игра задается матрицей

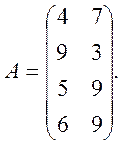
В новой игре первый игрок имеет четыре чистые стратегии, а второй − две. Нижняя цена игры  а верхняя цена игры .

Так как , то у этой игры нет седловой точки, поэтому нужно искать ее решение в смешанных стратегиях.  Пусть  − вектор смешанных стратегий первого игрока, а − вектор смешанных стратегий второго игрока. Платежная функция данной игры равна:

Второй игрок имеет две чистые стратегии, поэтому графически будет решаться задача второго игрока. Построения выполняются аналогично п.1, если поменять местами первого и второго игроков (см. рисунок 1.4). Цель второго игрока, согласно его осторожному поведению, состоит в минимизации его возможного риска. Риск второго игрока (т.е. максимально возможный проигрыш второго игрока при применении им той или иной смешанной стратегии) на рисунке 1.4 показан жирной линией. Точка  M обозначает  минимальный риск второго игрока. Она лежит на пересечении отрезков, соответствующих второй и четвертой чистым стратегиям первого игрока.

Обозначим оптимальную смешанную стратегию второго игрока . Для нахождения значений  и  воспользуемся утверждением 3. Активными стратегиями первого игрока являются вторая и четвертая. Тогда

   1) ,  => .

   2) , =>.

Приравняем эти значения к цене игры  и добавим уравнение , получим систему уравнений:

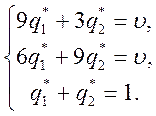
Решив эту систему, получаем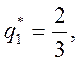   

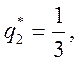
Теперь найдем оптимальную смешанную стратегию первого игрока, . Так как его активные стратегии − вторая и четвертая, а первая и третья пассивные, то . Следовательно,  .  Применяя утверждение 3 и учитывая, что цена игры уже найдена, получим систему уравнений:

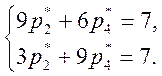
   Решая эту систему, получаем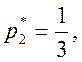

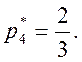
Итак, решение матричной игры задается векторами 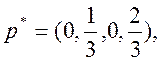 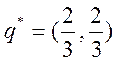и ценой игры :

	,  .

 

Задача 2.  Об оптовой закупке при неопределенности розничной продажи.

1. Составим платежную матрицу игры, описывающей предложенную в задаче ситуацию.  Эта задача  является примером так называемых «игр с природой». Торговая фирма выступает в качестве первого игрока. У нее есть две чистые стратегии: делать закупки, рассчитывая на холодную и дождливую погоду (первая стратегия) или на жаркую солнечную (вторая стратегия).  Вторым игроком является природа. У нее также две чистые стратегии. Первая стратегия − установить холодную и дождливую погоду,  вторая стратегия − установить жаркую солнечную погоду. Элементы платежной матрицы  − это прибыль, которую будет получать фирма в той или иной ситуации. Прибыль рассчитывается как разница между выручкой фирмы от розничной реализации продукции и ежедневными затратами фирмы. Затраты в свою очередь есть сумма средств, направленных на оптовую закупку товаров, и издержек на розничную реализацию продукции.

Рассмотрим первую чистую стратегию фирмы. Пусть фирма планирует закупить товары А и В в количествах k_A и  k_B соответственно. Предполагается, что завтра будет холодная погода.  Исходя из статистических данных, на каждые 2 ед. товара А реализуется 3 ед. товара В. Следовательно, фирма должна закупить продукты таким образом, чтобы выполнялось соотношение на их количество. Это значит, что должно выполняться соотношение:

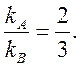
На закупки фирма предполагает тратить 9775 руб. ежедневно. Поэтому, исходя из оптовых цен продуктов, она может купить продукты в количествах, для которых выполнено:

Итак, для нахождения количеств закупаемых в расчете на холодную погоду продуктов, необходимо решить следующую систему уравнений:

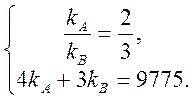
Отсюда получаем: k_A = 1150  k_B= 1725, т.е. необходимо закупить 1150 ед. товара А и  1725 ед. товара В.

Пусть фирма применяет свою вторую чистую стратегию, т.е. делает покупки в расчете на солнечную погоду. Это значит, что фирма  предполагает на каждые 5 ед. товара А продать 1 ед. товара В. Следовательно, для количеств n_A и n_Bзакупаемых товаров должно выполняться соотношение:

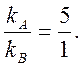
Учитывая оптовые цены товаров и планируемую сумму трат на их закупку, получаем систему уравнений:

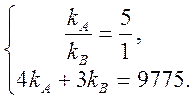
Решение этой системы: k_A = 2125,  k_B= 425. Итак, при второй своей чистой стратегии фирма должна закупить 2125 ед. товара А и  425 ед. товара В.

Теперь рассчитаем ожидаемую прибыль фирмы при различных погодных условиях. Может быть четыре ситуации:

1)  фирма применяла свою первую чистую стратегию, т.е. делала закупки в расчете на холодную погоду и угадала;