Сопротивление материалов. Часть 3: Методические указания к выполнению контрольных работ

СОПРОТИВЛЕНИЕ  МАТЕРИАЛОВ

ЧАСТЬ  3

ОМСК  2007

Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

Омский государственный университет путей сообщения

––––––––––––––––––

СОПРОТИВЛЕНИЕ  МАТЕРИАЛОВ

Часть 3

Утверждено редакционно-издательским советом университета в качестве
методических указаний к выполнению контрольных работ студентами
всех специальностей, изучающими курс сопротивления материалов

Омск 2007

УДК 593.3/6(076.5)

ББК 30.121я73

         С64

Сопротивление материалов. Часть 3: Методические указания к выполнению контрольных работ студентами всех специальностей, изучающими курс сопротивления материалов / В. К. Окишев, С. П. Андросюк, А. В. Климович,
С. А. Ступаков,  А. Г. Патеюк;  Омский  гос.  ун-т  путей  сообщения.  Омск, 2007. 31 с.

Методические указания содержат основные теоретические сведения
по изучаемым разделам курса сопротивления материалов и примеры решения типовых задач с подробными математическими выкладками и пояснениями,
а также основные теоретические зависимости и понятия, необходимые для
успешного самостоятельного решения каждой индивидуальной задачи.

Предназначены для студентов первого и второго курсов очной и заочной форм обучения специальностей 150800 – «Вагоны», 100700 – «Промышленная теплоэнергетика», 190200 – «Приборы и методы контроля качества и
диагностики», 150700 – «Локомотивы», 181400 – «Электрический транспорт железных дорог», 101800 – «Электроснабжение на железных дорогах», 210700 – «Автоматика, телемеханика и связь на железнодорожном транспорте».

Библиогр.: 4 назв. Табл. 1. Рис. 14.

Рецензенты: доктор техн. наук, профессор А. М. Завьялов;

                        доктор техн. наук, профессор В. А. Николаев.

________________________

© Омский гос. университет

путей  сообщения,  2007

ОГЛАВЛЕНИЕ

Введение.    5

1. Расчеты на прочность и жесткость плоских рам..    6

1.1. Основные теоретические сведения.    6

1.2. Решение типовой задачи.    6

2. Расчет на прочность валов при совместном действии изгиба и кручения. 12

2.1. Основные теоретические сведения. 12

2.2. Решение типовой задачи. 13

3. Расчет сжатых стержней на устойчивость. 17

3.1. Основные теоретические сведения. 17

3.2. Решение типовой задачи. 19

4. Динамическое действие нагрузок. 23

4.1. Основные теоретические сведения. 23

4.2. Решение типовой задачи при ударных воздействиях на конструкцию.. 24

4.3. Решение типовой задачи при равноускоренном вращении конструкции. 27

Библиографический список. 30

ВВЕДЕНИЕ

В соответствии с учебной программой и формой обучения студенты специальностей 150800, 100700, 190200, 150700, 181400 и 210700 должны выполнить определенное количество контрольных работ.

Настоящие методические указания предназначены для помощи студентам при выполнении ими контрольных работ по дисциплинам «Сопротивление материалов», «Прикладная механика», «Механика» по второй части курса.

Число контрольных работ, их содержание, индивидуальные схемы задач и конкретные значения геометрических размеров и физических величин, необходимые для решения, приведены в заданиях на контрольные работы «Сопротивление материалов» [1].

В данных методических указаниях содержатся необходимые теорети-ческие сведения, подробно изложены все этапы решения типовых задач
контрольных работ по каждому изучаемому разделу курса сопротивления материалов и проведен анализ решения задач. Все это способствует успешному
усвоению изучаемой дисциплины и решению задач контрольных работ.

1. Расчеты  на  прочность  и  жесткость  плоских  рам

1.1. Основные теоретические сведения

Рамой называется конструкция, образованная несколькими жестко соединенными между собой прямолинейными стержнями.

Если все стержни, образующие раму, и внешняя нагрузка лежат в одной плоскости, то рама называется плоской (рис. 1.1).

В отличие от изгиба балок [4] в сечениях плоских рам возникает дополнительное внутреннее усилие – продольная сила N.

Продольная сила в произвольном сечении рамы равна алгебраической сумме всех внешних сил, лежащих по одну сторону от проведенного сечения и направленных вдоль оси рассматриваемого стержня рамы. Растягивающая сила принимается со знаком «плюс», сжимающая – со знаком «минус».

Два других внутренних усилия – поперечная сила Q_y и изгибающий момент – вычисляются аналогично внутренним усилиям при изгибе балок [3]. Следует лишь учесть, что для рамы изгибающий момент положителен, если растянуты внутренние волокна рассматриваемого участка.

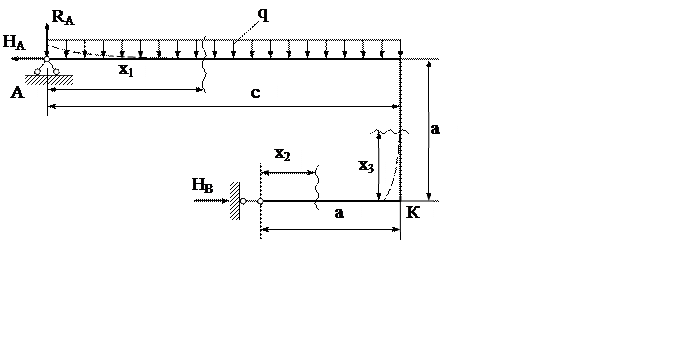
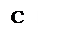
Рис. 1.1. Расчетная схема плоской рамы

1.2. Решение типовой задачи

Для заданной плоской рамы (см. рис. 1.1) записать выражения для расчета внутренних усилий N, Q_y и момента M_z в общем виде по участкам, построить эпюры N, Q_y и M_z, найти M_{z max}, подобрать круглое поперечное сечение при
[σ] = 160·10³ кН/м², определить вертикальное перемещение точки  В, используя универсальный метод Мора (вычисляя интегралы по способу Симпсона). Руководствуясь расчетом и эпюрой изгибающих моментов, показать приблизительный вид изогнутой линии стержней рамы.

Принять: q = 10 кН/м; а = 2 м; с = 4 м.

Решение.

Определяем реакции опор с помощью уравнений равновесия:

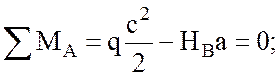                                                  (1.1)

                                                         (1.2)

                                       (1.3)

Из уравнений (1.1) – (1.3) соответственно находим:   и

Для проверки правильности нахождения значений H_A и H_B составляем дополнительное уравнение равновесия:

                                                         (1.4)

После подстановки полученных данных в уравнение (1.4) получаем:  следовательно, реакции найдены верно.

Рама состоит из трех стержней. На каждом стержне проводим сечение, определяемое координатами x₁, x₂, x₃ (условимся для всех стержней ось x нап-равлять вдоль стержня). Запишем уравнения внутренних усилий по участкам.

Первый участок:  .

;       (1.5)      ;      (1.6) 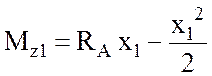    .                                  (1.7)

При  x₁ = 0  кН; кН;  . При x₁ = 4  кН; ;  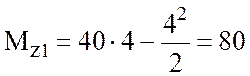(кН·м).

Третью точку для построения эпюры M_z возьмем посредине участка.

При x₁ = 2 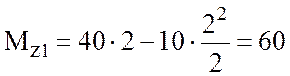  (кН·м).

Второй участок:   .

       ;         (1.8)           ;           (1.9)                            (1.10)

Третий участок:   .

         ;          (1.11)        ;       (1.12)                  (1.13)

При  х₃ = 0    При  х₃ = 2   (кН·м).

По результатам расчета построим эпюры внутренних сил (рис. 1.2).

 

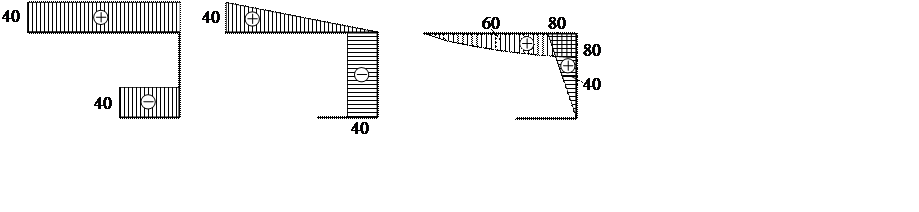а                                                 б                                                в

Рис. 1.2. Эпюры внутренних усилий:

N, кН (а); Q_y, кН (б); M_z, кН×м (в)

При построении эпюр N и Q_y положительные ординаты откладываем
с внешней стороны рамы, отрицательные – с внутренней. Эпюру изгибающих моментов строим со стороны растянутых волокон.

Для проверки правильности построения эпюр вырежем бесконечно малый элемент из узла рамы и приложим к нему все внутренние и внешние усилия (рис. 1.3).

Проверим равновесие узлов, составив уравнения равновесия:

Узел С:                               

Узел К:            

Проверка показала, что узлы находятся в равновесии, следовательно, эпюры построены верно.

 

а                                                     б