Сопротивление материалов. Часть 3: Методические указания к выполнению контрольных работ, страница 5

Найдем статическое вертикальное перемещение (прогиб) точки удара. Для этого выбираем вспомогательное единичное состояние, приложив в точку удара единичную нагрузку. Вспомогательная эпюра изгибающих моментов  (рис. 4.1, д) будет иметь тот же вид, что и эпюра , следует лишь все ординаты эпюры  уменьшить в 300 раз. Перемножим эпюры и по формуле Симпсона (4.3) [2]:

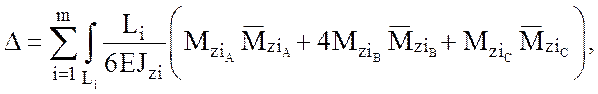                                                                               (4.6)

где – ординаты изгибающих моментов по концам и посредине каждого участка эпюры M_zi;

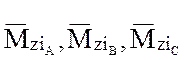 – соответствующие ординаты эпюры ;

– модуль упругости стали первого рода (модуль Юнга).

Подставляя в формулу (4.6) соответствующие значения L, J и  для
участков балки AB и BC, получим:

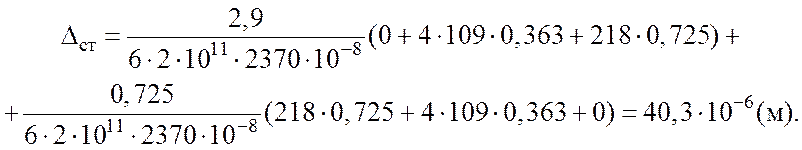
Вычислим коэффициент динамики (4.4):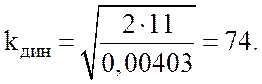

Наибольшие нормальные напряжения в балке рассчитаем согласно выражению (4.3):  (МН/м²).

2) Заменим правую опору балки пружиной (рис. 4.1, е). Установленная пружина увеличивает статическую деформацию в точке удара. В месте установки пружины действует сила  равная 375 Н (0,375 кН), вызывающая осадку точки В, которая рассчитывается по формуле:

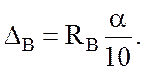                                                                     (4.7)

Из подобия двух треугольников (см. рис. 4.1, е)

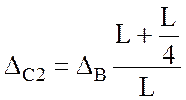                                              .                 (4.8)

После подстановки исходных данных в формулы (4.7), (4.8) получим:

 

C

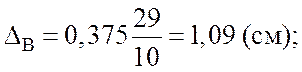
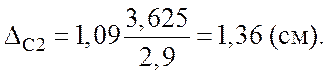
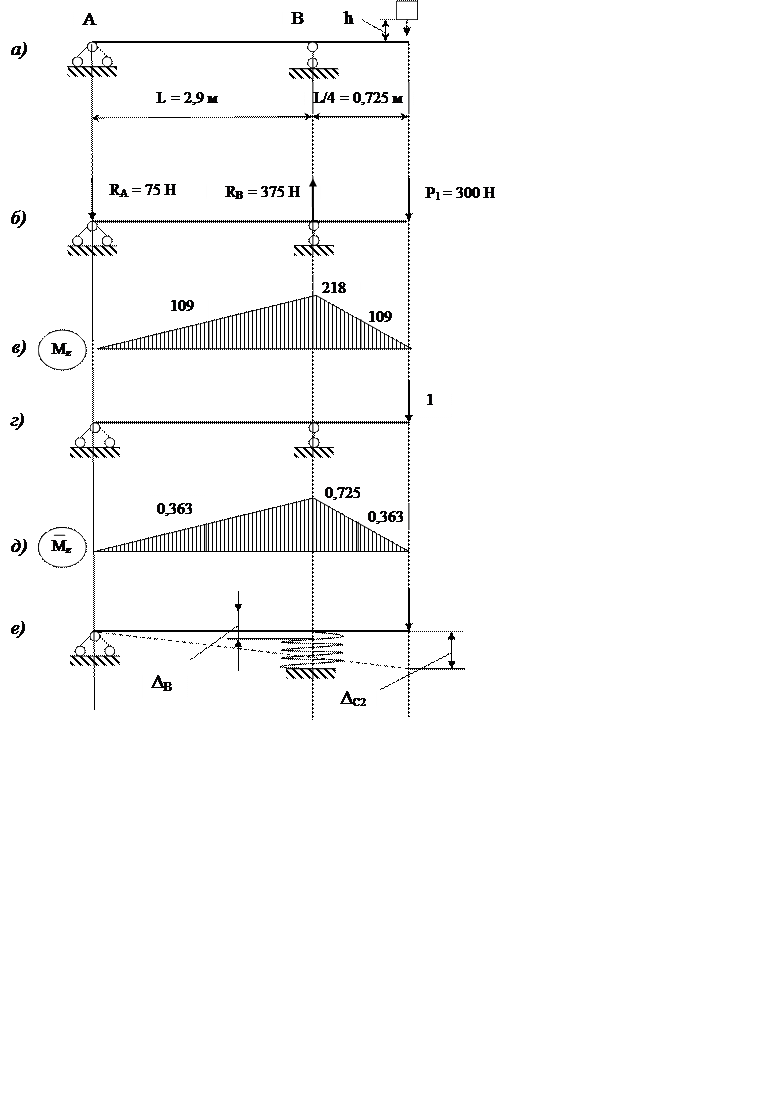
Рис. 4.1. Схематическое представление ударного воздействия нагрузки на балку:

а, б, г, е – расчетные схемы; в, д – эпюры изгибающих моментов

Полное перемещение точки удара определяется как сумма прогиба балки из первого решения и значения : 

В этом случае новый коэффициент динамики вычисляется по формуле:

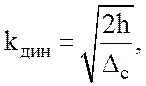                                                                     (4.9)

наибольшие нормальные напряжения –

                                                              (4.10)

После подстановки исходных данных в формулы (4.9), (4.10) получим: 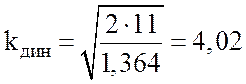;  (МН/м²).

Сравнение значений напряжений, полученных в двух вариантах решения задачи, показывает, что при замене правой опоры пружиной нормальные
напряжения уменьшатся в 18,4 раза (68,1 : 3,7).

4.3. Решение типовой задачи при равноускоренном вращении конструкции

Стальной валик и жестко соединенный с ним ломаный стержень круглого поперечного сечения диаметром d вращается с постоянной частотой n вокруг оси AB (рис. 4.2, а). Проверить прочность валика, если L = 15 см, d = 2,3 см, =100 МН/м², n = 1200 об/мин.

Решение.

1) Построим эпюры изгибающих моментов  от возникающих на участках CD и DE сил инерции.

При вращении системы ускорения всех частиц элемента DE одинаковы и равны  (радиусом вращения является длина участка CD), где в соответствии с формулой (4.2) угловая скорость вращения валика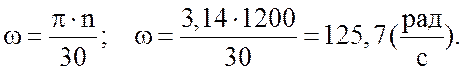

Масса элемента DE рассчитывается по формуле:

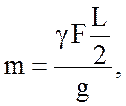                                                                      (4.11)

где  – вес элемента DE, так как 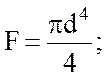 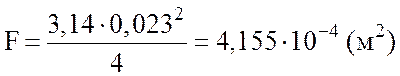– площадь сечения; – удельный вес материала стержня;

g – ускорение свободного падения, g = 9,81 м/с².

По формуле (4.1) найдем силу инерции, действующую на элемент DE:

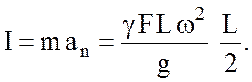                                                    (4.12)

Обозначим в выражении (4.12)

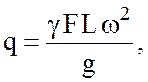                                                                   (4.13)

тогда суммарную инерцию участка DE можно рассматривать как равномерно распределенную нагрузку интенсивности 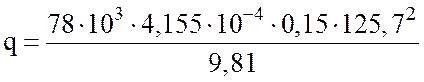 =  (рис. 4.2, б).

Ускорения элемента CD переменны. Для точки С радиус вращения (следовательно,  ускорение) обращается в ноль, соответственно в этой точке равна нулю и сила инерции. Для точки D силы инерции те же, что и для участка DE. Следовательно, можно считать силы инерции на участке CD распределенными по закону треугольника с результирующей 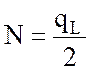 (как площадь треугольника эпюры сил инерции на участке CD).

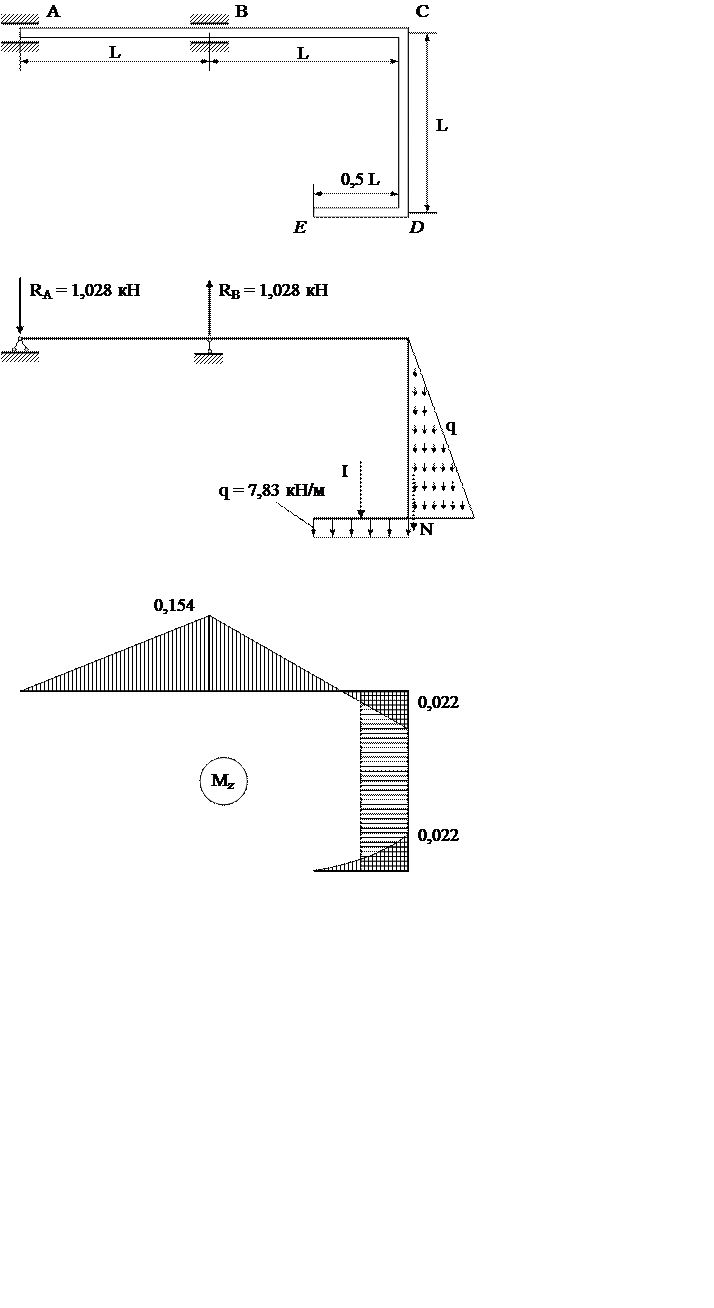
Таким образом, всю систему можно рассматривать как плоскую раму,
нагруженную равномерно распределенной нагрузкой q и сосредоточенной силой N. Порядок решения такой задачи приведен в методических указаниях [2, подразд. 4.2, 4.3]. Методом сечений строим эпюру изгибающих моментов (рис. 4.2, в).

 

а

б

в

Рис. 4.2. Нагрузки и изгибающий момент:

а – заданная схема; б – расчетная схема; в – эпюра изгибающих моментов

2) Произведем проверку прочности валика.

Условие прочности на изгиб запишется в виде:

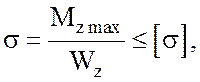                                                           (4.14)

где = 0,154 кН·м – максимальный изгибающий момент в опасном сечении валика (см. рис. 4.2, в);

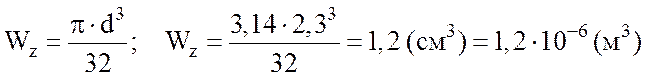 – осевой момент сопротивления круглого сечения валика.

Тогда максимальные нормальные напряжения в опасном сечении

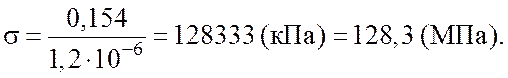
Таким образом, нормальные напряжения в валике оказались больше допустимых (=100 МН/м²), следовательно, условие прочности не выполняется. Заданный валик нельзя использовать при заданной частоте вращения, поэтому необходимо либо увеличить его диаметр, либо использовать при изготовлении валика более прочную сталь.

Библиографический список

1. Сопротивление материалов / В. К. Окишев, С. П. Андросюк и др. / Омский гос. ун-т путей сообщения. Омск, 2007. Ч. 1. 24 с.

2. Сопротивление материалов / В. К. Окишев, С. П. Андросюк и др. / Омский гос. ун-т путей сообщения. Омск, 2007. Ч. 2. 33 с.

3. Смирнов А. Ф. Сопротивление материалов / А. Ф. Смирнов,
А. В. Александров, Н. И. Монахов. М.: Высшая школа, 2000. 320 с.

4. Степин П. А. Сопротивление материалов / П. А. Степин. М.: Высшая школа, 2001. 380 с.