Сопротивление материалов. Часть 3: Методические указания к выполнению контрольных работ, страница 2

Рис. 1.3. Схематическое изображение проверки равновесия узлов С (а) и К (б)

Поперечное сечение стержней рамы выбираем по условию прочности:

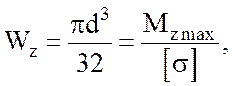                                                       (1.14)

отсюда 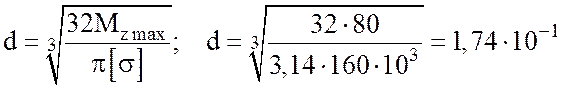(м) = 17,4 (см).

Значение берем из эпюры изгибающих моментов (см. рис. 1.2).

Определяем осевой момент инерции стержней рамы:

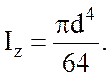                                                                        (1.15)

После подстановки данных в уравнение (1.15) получаем: 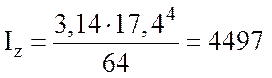(см⁴) = 0,4497·10^-4 (м⁴).
          Жесткость стержней рамы   (кН×м²).

Для вычисления вертикального перемещения сечения В выберем вспомогательное состояние рамы, отбросив в заданной схеме рамы (см. рис. 1.1) внешние нагрузки и приложив в точке В вертикальную вспомогательную силу, равную единице (рис. 1.4, а).

Построим для вспомогательного состояния рамы эпюру изгибающих моментов . Найдем новые реакции опор:

                                                     (1.16)

                                          (1.17)

                                                   (1.18)

отсюда    

Для проверки правильности нахождения значений опорных реакций
составляем дополнительное уравнение равновесия:

следовательно, реакции опор найдены верно.

 

а                                                              б

Рис. 1.4. Вспомогательное состояние рамы:

а – расчетная схема;  б – эпюра

Запишем уравнения изгибающего момента  по участкам рамы:

Первый участок: 

  При  х₁ = 0  0.  При  х₁ = 4 

Второй участок:  

  При  х₂ = 0    При  х₂ = 2  

Третий участок:  

   При  х₃ = 0    При  х₃ = 2 

По результатам расчета построим эпюру (см. рис. 1.4, б).

Перемещение сечения В найдем по формуле Симпсона:

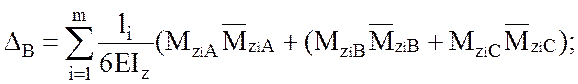                                                                                (1.19)

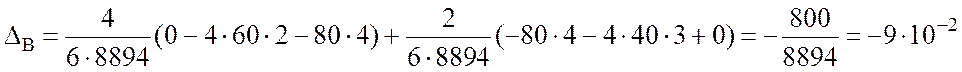(м).

Напомним, что при вычислении  произведения ординат M_z и  были записаны с отрицательным знаком, так как значения ординат были отложены
в разные стороны от стержней рамы.

Отрицательный ответ указывает на то, что действительное перемещение сечения В происходит в противоположную направлению выбранной вспомо-гательной единичной нагрузки сторону. Примерный вид изогнутой линии стержней рамы показан на рис. 1.5 пунктирной линией.

B

Рис. 1.5. Схематическое изображение деформации стержней рамы

2. Расчет  на  прочность  валов  при  совместном  действии
изгиба  и  кручения

2.1. Основные теоретические сведения

В первой части курса сопротивления материалов основное внимание уделено решению задач, в которых прямолинейные стержни испытывают отдельные виды деформации: растяжение, сжатие, кручение, изгиб. На различные
детали машин часто одновременно действуют несколько из указанных видов деформации. Такой случай работы деталей получил название сложного сопротивления. Наиболее распространенным случаем сложного сопротивления является совместное действие изгиба и кручения.

Для расчета на прочность стержня при совместном действии изгиба и кручения строят на отдельных рисунках эпюры вертикального M_z и горизонтального M_y изгибающих и крутящего M_х моментов [2]. В качестве опасного сечения стержня принимают сечение, в котором ординаты всех моментов наибольшие, либо расчет проводят для нескольких сечений, где один или два момента достигают максимального значения. Стержень считается прочным, если выполняется условие:

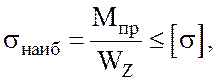                                                           (2.1)

где – приведенный момент, вычисляемый по одной из теорий прочности [3];

 –  момент сопротивления поперечного сечения;

 –  допустимое нормальное напряжение материала стержня.

По третьей теории прочности приведенный момент

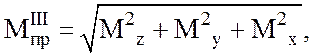                                             (2.2)

по четвертой –

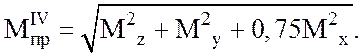                                      (2.3)

2.2. Решение типовой задачи

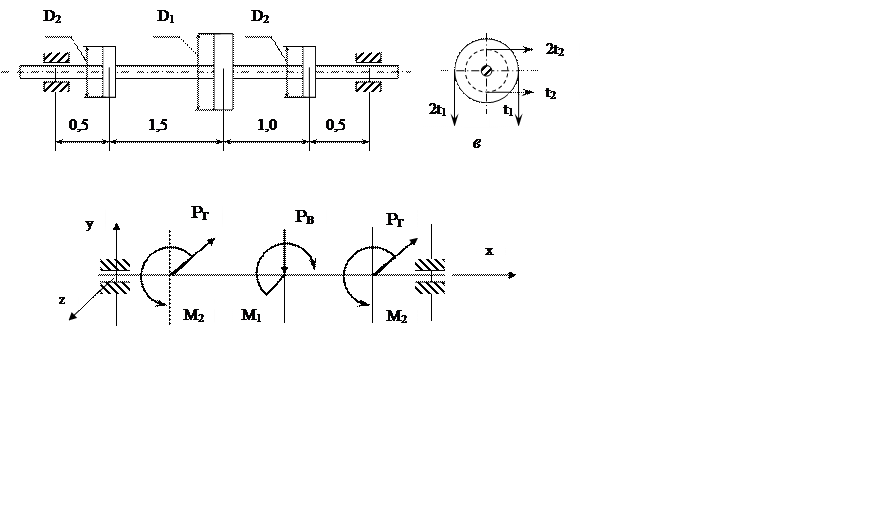
Шкив диаметром D₁  с ветвями, направленными вертикально, вращается с угловой скоростью w и передает мощность N. Два других шкива имеют одинаковый диаметр D₂ и ветви ремня, направленные горизонтально, каждый из шкивов передает мощность 0,5N (рис. 2.1).

Определить моменты, приложенные к шкивам, окружные усилия, составляющие давления на вал, максимальный расчетный момент; построить эпюры крутящих и изгибающих моментов от горизонтальных и вертикальных сил, эпюру суммарных изгибающих моментов; подобрать диаметр вала.

Исходные данные для решения задачи: D₁ = 1 м; D₂ = 0,5 м;   рад/с;
N = 50 кВт.

а

б

Рис. 2.1. Вал ременной передачи

а – схема вала;  б – расчетная схема;  в – схема вала (вид сбоку)

Решение.

1) Вычислим моменты, приложенные к шкивам.

Крутящий момент определим по заданным величинам – N и :

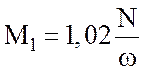                       ;                  (2.4)                 .                              (2.5)

После подстановки исходных данных в уравнения (2.4) и (2.5) получи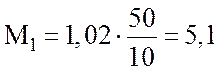м:  (кН·м); кН·м.

2) Построим эпюру крутящих моментов.

Расчетная схема вала приведена на рис. 2.2, а. Концы вала закреплены
в подшипниках, которые практически не мешают валу свободно поворачиваться, поэтому реактивные моменты в подшипниках не возникают, и эпюру крутящих моментов можно построить только для средних участков. Порядок
построения эпюры M_х приведен в методических указаниях [2].

3) Определим окружные усилия t₁ и t₂.

Окружные усилия относительно центра вала создают момент, значение которого должно равняться значению соответствующего крутящего момента.

Для шкива 1 получим: