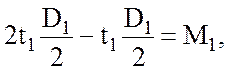Сопротивление материалов. Часть 3: Методические указания к выполнению контрольных работ, страница 3

                                                         (2.6)

отсюда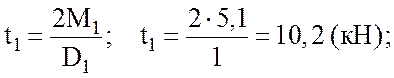

для шкива 2 –

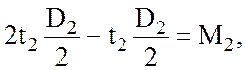                                                       (2.7)

отсюда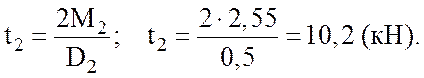

4) Определим давления P₁ и P₂ на вал (см. рис. 2.2, в, д).

Общее вертикальное усилие

                                                             (2.8)

Общее горизонтальное усилие

                                                           (2.9)

После подстановки данных в уравнения (2.8) и (2.9) получим:  

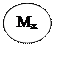
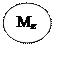
Рис. 2.2. Эпюры внутренних усилий на валу

 а, в, д – расчетные схемы; б, г, е, ж – эпюры моментов

5) Построим эпюру изгибающих моментов от горизонтальных и вертикальных сил.

Силы P₁ и P₂ вызывают изгиб в вертикальной и горизонтальной плос-костях, при этом подшипники могут рассматриваться как обычные балочные опоры (см. рис. 2.2, в, д).

Порядок построения эпюр изгибающих моментов M_z и M_y изложен в
методических указаниях [2].  Вид эпюр M_z и M_y приведен на рис. 2.2, г, е.

6) Построим эпюру суммарных изгибающих моментов.

Ординаты  суммарной эпюры изгибающих моментов М_и находим
по формуле:

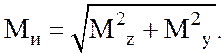                                                        (2.10)

Например, для сечения при x = 2 м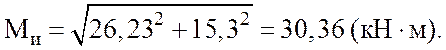 

Эпюра М_и изображена на рис. 2.2, ж (следует обратить внимание на то, что согласно формуле (2.10) эпюра М_и криволинейна).

7) Найдем величину максимального расчетного момента по третьей теории прочности.

Вид эпюр M_х и М_и указывает на то, что опасным является сечение, расположенное на расстоянии 2 м от левой опоры, для которого  

Расчетный момент находим по выражению (2.2) с учетом формулы (2.10):

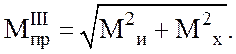                                                      (2.11)

После подстановки полученных данных в уравнение (2.11) получим: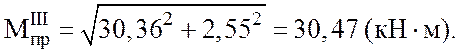

8) Подберем диаметр вала при  = 70 МН/м².

Из условия прочности (2.1) находим требуемое значение момента сопротивления:

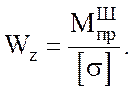                                                                     (2.12)

После подстановки полученных данных в уравнение (2.12) получим: 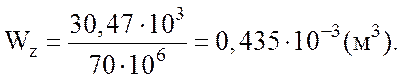 Для круглого сечения 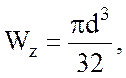 отсюда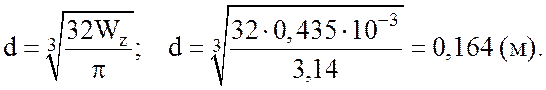

Согласно рекомендациям, приведенным в методических указаниях
[2, подразд. 2.2], округляем значение найденного диаметра d до 170 мм.

3. Расчет  сжатых  стержней  на  Устойчивость

3.1. Основные теоретические сведения

Устойчивостью называется способность тела при действии на него внешних нагрузок сохранять первоначальное положение равновесия.

Сила, при превышении которой стержень теряет устойчивость, называется критической силой, обозначается она Р_кр.

Понятие устойчивости связано с характеристикой стержня, получившей название гибкости. Гибкими называют стержни, у которых размеры поперечного сечения значительно меньше длины стержня.

Гибкость стержня определяется по формуле:

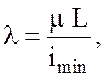                                                                           (3.1)

где L – длина стержня;

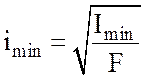 – минимальный размер инерции сечения;

 – минимальный момент инерции сечения;

F – площадь сечения.

В реальных условиях существуют несколько вариантов закрепления концов стержней, наиболее распространенные из них представлены на рис. 3.1, где для каждого варианта показана форма потери устойчивости и приведено значение коэффициента закрепления концов стержня .

По значению гибкости  принято разделять стержни на три класса. Для каждого класса значение критической силы Р_кр вычисляется по определенной формуле.

1) Стержни большой гибкости,  > 100.

Критическая сила вычисляется по формуле Эйлера:

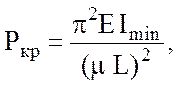                                                                 (3.2)

где Е – модуль упругости материала.

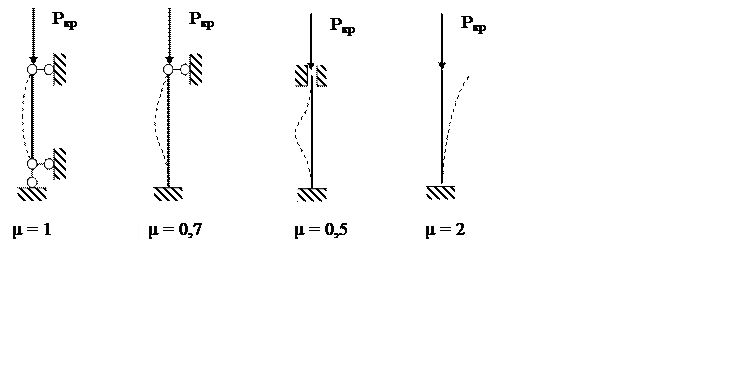      а                             б                             в                г

Рис. 3.1.  Варианты закрепления стержней

2) Стержни средней гибкости, .

Критическая сила рассчитывается по формуле Ясинского:

                                                               (3.3)

где а, b – постоянные, определяемые опытным путем для заданного материала; для стали  .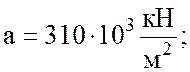

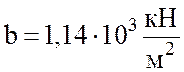3) Стержни малой гибкости,  < 40.

В этом случае стержень не теряет устойчивости и работает в условиях простого сжатия, а критическая сила

                                                   ,                      (3.4)

где– предел текучести материалов, для стали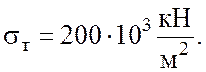

Допускаемая сила в задачах на определение устойчивости должна быть меньше Р_кр:

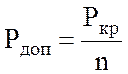                                                  ,                     (3.5)

где n  – коэффициент запаса устойчивости, n > 1.

Допускаемую силу можно вычислять на основании условия устой-чивости:

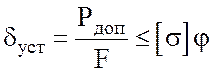                                            ,               (3.6)

где –  допускаемое напряжение материала на сжатие;

 – коэффициент снижения допускаемого напряжения (), определяется он по справочной таблице.

Зависимость значения коэффициента  от гибкости стержня

Гибкость стержня	0	10	20	30	40	50	60	70	80	90	100
Значение  для стали Ст3	1	0,99	0,96	0,94	0,92	0,89	0,86	0,81	0,75	0,69	0,60
Гибкость стержня	110	120	130	140	150	160	170	180	190	200
Значение  для стали Ст3	0,52	0,45	0,40	0,36	0,32	0,29	0,26	0,23	0,21	0,19

3.2. Решение типовой задачи

Стальной стержень, длина L которого равна 1 м, сжимается силой Р_кр.
Условия закрепления концов стержня показаны на рис. 3.2 ( = 2). Определить коэффициент запаса устойчивости n.