Основы работы в автоматизированной системе Mathcad: Методические указания к выполнению лабораторных работ по информатике, страница 8

Более надежным способом выполнения символьных преобразований является использование специальных команд для решения определенных задач из меню Символика. Рассмотрим их применение на конкретных примерах.

Пример 1. Упростить выражение   (a² – b²)/(a + b).

Для решения этой задачи нужно набрать исходное выражение, заключить его в уголковый курсор, затем выполнить команду меню Символика → Упростить. Результат работы представлен на рис. 15.

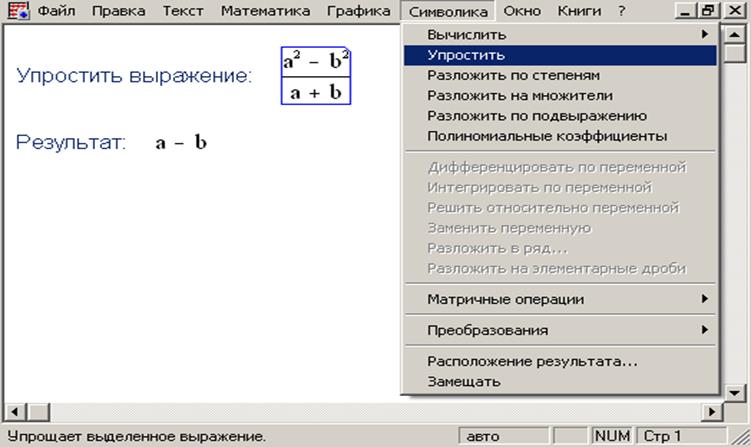
Рис. 15. Пример упрощения выражения

Команду Упростить можно применять не только для всего выражения целиком, но и для отдельной его части, помещенной в уголковый курсор.

Аналогично выполняются символьные команды разложения выражения по степеням, на множители, на элементарные дроби, вычисления пределов и др.

Пример 2. Проинтегрировать выражение x²∙e^x по переменной x.

Способ 1. Использование символьного оператора вычисления неопределенного интеграла:

1) с помощью кнопки  палитры операторов математического анализа  вводим в документ знак интеграла    ;

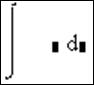2) вводим подынтегральное выражение x²∙e^x в соответствующий слот;

3) вводим переменную интегрирования x после символа «d»;

4) заключаем все выражение в уголковый курсор и вводим знак символьного равенства с помощью кнопки  :  ;

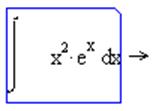5) выполняем щелчок вне области формулы, после чего Mathcad выводит результат символьного вычисления:  .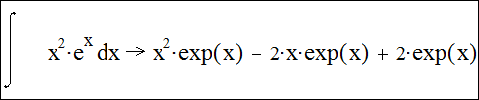

Способ 2. Использование меню Символика:

1) набираем подынтегральное выражение;

2) устанавливаем курсор в любом месте выражения на переменной интегрирования x (при этом можно заключить переменную в уголковый курсор, а можно просто установить на нее курсор ввода данных);

3) выполняем команду Символика → Интегрировать по переменной.

Способ 3. Использование меню ? → Шпаргалки → Математический анализ → Символьное интегрирование, где в окошко заготовки вводим подынтегральное выражение.

Пример 3. Продифференцировать выражение x²∙e^x по переменной x.

Способ 1. Использование символьного оператора производной .

Способ 2. Использование меню Символика → Дифференцировать по переменной.

Способ 3. Использование меню ? → Шпаргалки → Математический анализ → Символьное нахождение производной.

Все способы дифференцирования выполняются аналогично интегри-
рованию.

Для вычисления производных более высокого порядка можно применять оператор  (по способу 1), повторно дифференцировать выражение для производной низшего порядка (по способу 2), использовать специальную заготовку в Шпаргалках (по способу 3).

ВНИМАНИЕ! При выполнении символьных вычислений следует иметь в виду важное различие между символьным преобразованием, использующим меню Символика, и преобразованием с использованием символьного знака равенства. Результаты с правой стороны от символьного знака равенства вычисляются заново каждый раз при внесении изменений в рабочий документ. Результат, полученный с использованием меню Символика, модифицироваться не будет (при изменении исходных данных все такие преобразования нужно выполнить заново).

3.2. Лабораторная работа 3

Цель работы: изучение различных способов выполнения символьных вычислений.

Задание 1. Упростить выражение, заданное в графе 2 табл. 6.

Задание 2. Тремя способами найти первообразную, первую и вторую производную для функции, приведенной в графе 3 табл. 6. Текстовую часть работы оформить по образцу рис. 9 с использованием материала Шпаргалок.

Таблица 6

Исходные данные для символьных вычислений

Продолжение табл. 6

1	2	3
2
3  2
4
5
6
7
8
9
10
11

Окончание табл. 6

1	2	3
12
13
14
15
16

Библиографический список

1.  MATHCAD 6.0 PLUS. Финансовые, инженерные и научные расчеты в среде Windows 95: Пер. с англ. М.: Филинъ, 1996. 712 с.

2.  Информатика. Базовый курс. 2-е изд. / Под ред. С. В. Симоновича. СПб: Питер, 2005. 640 с.