Основы работы в автоматизированной системе Mathcad: Методические указания к выполнению лабораторных работ по информатике, страница 7

Рис. 11. Пример табуляции функции

2.2. Построение графиков

Mathcad позволяет легко создать и затем отформатировать график функции, заданной для дискретного аргумента.

Рассмотрим построение графика на предыдущем примере функции y(x) = sin(x) (см. рис. 11). После задания диапазона изменения дискретного аргумента и определения функции для создания графика нужно выполнить следующие действия:

1) установить визир в месте размещения графика и выполнить команду меню Графика → Декартов график  или щелкнуть кнопку  палитры графиков. В результате в документе появится графическая область с незаполненными полями (рис. 12);

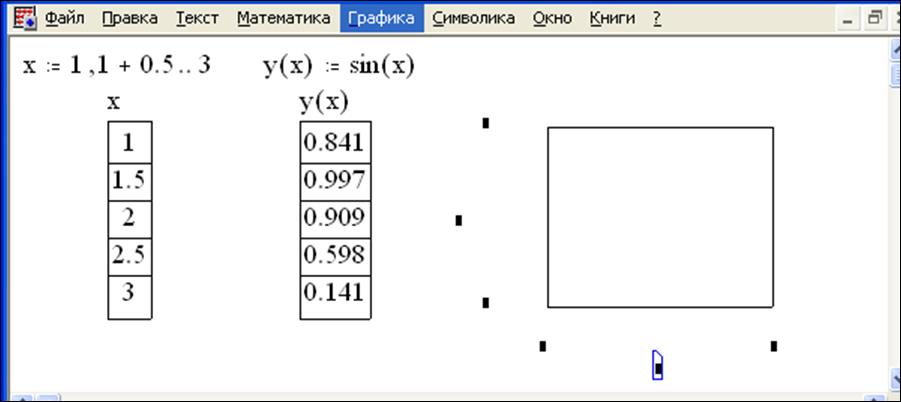
Рис. 12. Графическая область с незаполненными полями

2) в поле графика под осью абсцисс посередине задать имя дискретного аргумента x;

3) в поле графика слева от оси ординат посередине задать функцию y(x), для которой требуется построить график.

После щелчка на любом свободном месте вне графика Mathcad вычисляет и строит точки графика и устанавливает пределы по осям координат.

При построении графиков следует соблюдать те же правила размещения переменных, что и при вычислениях, т. е. исходные данные для графика должны быть записаны выше или слева от него.

Для построения нескольких графиков в одних координатных осях в поле ввода по оси ординат имена функций вводятся через запятую (при этом они будут располагаться друг под другом, а запятая на экране не отображается).
Mathcad допускает до 16 графиков в одной графической области.

Примеры построения графиков приведены на рис. 13.

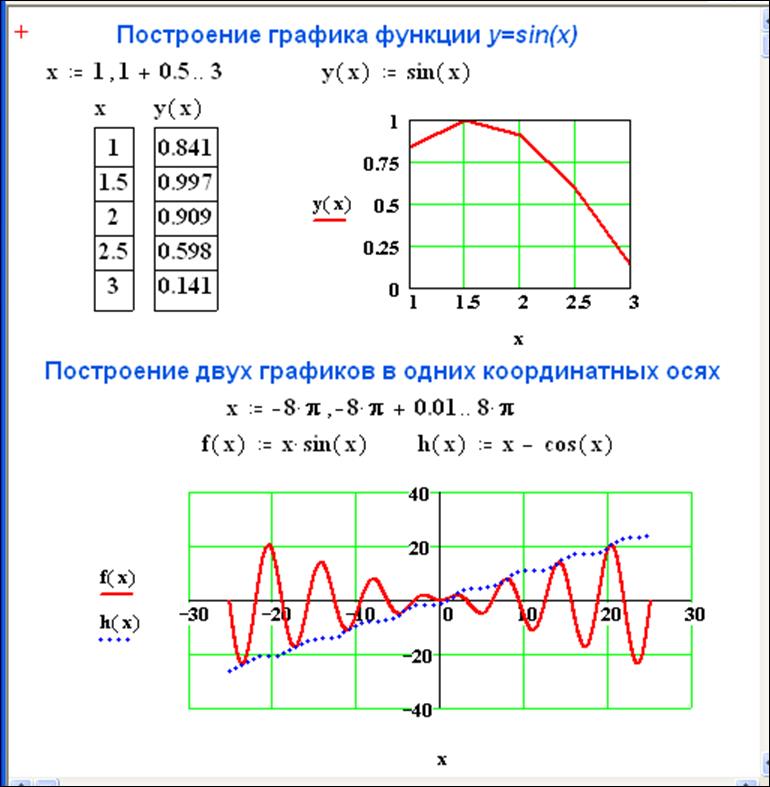
Рис. 13. Примеры построения графиков функций

Для изменения размера графика достаточно выделить его с помощью протягивания мыши (при этом область графика будет очерчена пунктирной рамкой) и растянуть его до желаемого размера.

Построенный график можно отформатировать: изменить тип, толщину и цвет линии, изобразить сетку, нанести риски на оси, сделать надписи и т. д. Диалоговое окно редактирования графика открывается двойным щелчком на графике и позволяет изменить доступные характеристики графика (рис. 14).

Аналогично электронным таблицам Excel система Mathcad обладает важным свойством автоматического пересчета результатов и изменения графиков в случае изменения исходных данных.

 

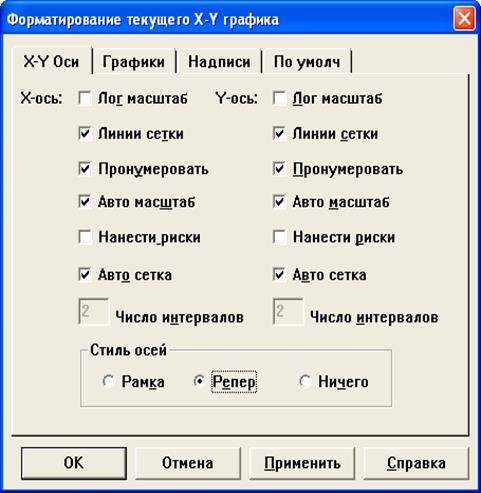
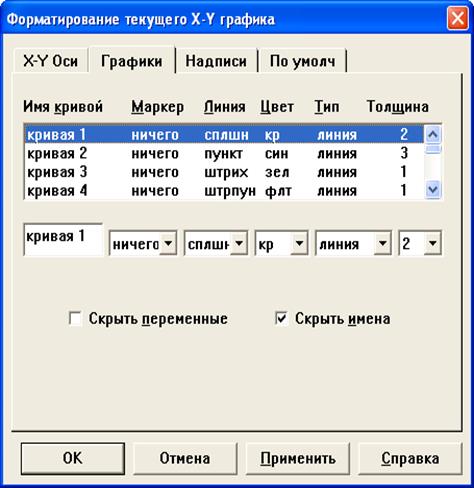
Рис. 14. Вкладки «Оси» и «Графики» диалогового окна форматирования графика

2.3. Лабораторная работа 2

Цель работы: изучение правил табуляции переменных, построения и форматирования графиков функций.

Задание. В соответствии с вариантом табл. 5 протабулировать функции и построить их графики сначала по отдельности, а затем в одной графической области. Вывести на экран таблицы значений дискретного аргумента и функций, в поле графиков изобразить линии сетки, для осей координат использовать стиль «репер». Текстовую часть работы оформить по образцу рис. 9, вычислительную и графическую – по образцу рис. 13.

Таблица 5

Исходные данные для табуляции функций и построения графиков

Вариант	Исходные данные	Диапазон и шаг изменения аргумента	Функции
1	m = 4,4; с = 1,27	-2 ≤ t ≤ 2; Dt = 0,25	,
2	y = 0,03	1 ≤ x ≤ 4; Dx = 0,5	,
3	b = 0,13	0 ≤ x ≤ 2; Dx = 0,25	,
4	b = 0,02; a = 1,1	0 ≤ x ≤ 1; Dx = 0,1	,
5	b = 3,2	0 ≤ x ≤ 2,5; Dx = 0,25	,
6	b = 1,15; a = 1,7	2 ≤ x ≤ 4; Dx = 0,25	,
7	b = –7,8; a= 2,25	0 ≤ t ≤ 2; Dt = 0,1	,
8	b= 3,7; m= –0,5	0 ≤ t ≤ 2; Dt = 0,1	,
9	b= 7,1; a= 1,5	1,3 ≤ x ≤ 2,5; Dx = 0,1	,
10	a= 0,25	1 ≤ x ≤ 2; Dx = 0,1	,
11	a= 1,79	0 ≤ x ≤ 5; Dx = 1	,
12	m= 1,5	1,5 ≤ x ≤ 4; Dx = 0,25	,
13	a= –0,15	0 ≤ x ≤ 3; Dx = 0,15	,
14	m= 0,75	0,1 ≤ x ≤ 2,7; Dx = 0,2	,
15	a= 3,3	0 ≤ x ≤ 2; Dx = 0,1	,
16	a= 0,75 b= –7,1	0,1 ≤ x ≤ 2,7; Dx = 0,2	,

3. СИМВОЛЬНЫЕ  ПРЕОБРАЗОВАНИЯ  И  ВЫЧИСЛЕНИЯ

3.1. Упрощение, интегрирование и дифференцирование выражений

При численных вычислениях результатом расчета является одно или несколько чисел. В символьной математике результатом вычисления выражения является другое выражение. Первоначальное выражение можно разложить на множители, упростить, проинтегрировать и т. д.

Для выполнения символьных вычислений рекомендуется исходное выражение заключить в уголковый курсор, ввести символьный знак равенства с помощью кнопки  на палитре простых операторов , затем щелкнуть мышью вне выражения. Однако при этом не всегда удается достичь желаемого результата. Причиной этого является большая сложность и неоднозначность символьных задач, в связи с чем необходимо соблюдать ряд ограничений, накладываемых на использование символьного знака равенства.