Основы работы в автоматизированной системе Mathcad: Методические указания к выполнению лабораторных работ по информатике, страница 5

Рассмотрим основные правила построения математических выражений и выполнения расчетов в Mathcad на конкретном примере.

Пусть нужно вычислить 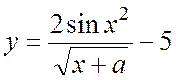    при a = 0,8;  x = 4,56.

В табл. 2 приведена последовательность действий для решения этой задачи, результат работы см. на рис. 4.

Пропущенные при вводе формулы символы можно вводить обычным образом, установив курсор в нужное место. Для вставки пропущенного операнда после имеющегося операнда нужно поместить в уголковый курсор имеющийся операнд, сначала ввести знак математической операции, а затем набрать пропущенный операнд. Вставка пропущенного операнда перед имеющимся операндом выполняется аналогично, за исключением того, что после заключения операнда в уголковый курсор нужно перейти в режим вставки символов, нажав клавишу Insert (при этом уголковый курсор изменит цвет с синего на красный, а срезанный угол будет слева).

Таблица 2

Пример ввода формулы и вычисления в Mathcad

Последовательность действий	Результат
Выводим на экран арифметическую палитру символов	см. рис. 2
Вводим исходные данные:  a  :1 0.8 ;   x  :1 4.56
Вводим    y , затем –   :1
Вводим   2  и знак умножения  *1
На арифметической палитре выбираем   (или из списка функций по кнопке выбираем sin(z))
Вводим x
На арифметической палитре выбираем   (или на клавиатуре нажимаем 1^1)
Вводим степень 2, затем четыре раза нажимаем 1↑1 для охвата всего числителя уголковым курсором
Вводим символ деления 1/1
На арифметической палитре выбираем символ
Вводим    x    +    a  , затем четыре раза нажимаем 1↑1 для охвата уголковым курсором всей дроби
Вводим с клавиатуры   –  и  51
На свободном месте листа для получения результата расчета набираем  y    =1	y = –4.196 (см. рис. 4)

1.4.3. Особенности вычислений в Mathcad

В ходе расчетов формулы обрабатываются последовательно слева направо и сверху вниз. Если расположить значение переменной ниже или правее формулы, в которую она входит, документ становится логически непоследовательным, что приводит к невозможности выполнения вычислений. Переменная в формуле является неопределенной и выделяется черным цветом (рис. 7).

Рис. 7. Пример неправильного расположения данных

Для исправления ошибки нужно просто выделить и переместить любую из областей определения – x или y, расположив их в логической последовательности (см. рис. 4).

Если на рабочем листе Mathcad какая-либо переменная была определена несколько раз, то в каждом конкретном месте документа в расчетах используется то ее значение, которое обработано Mathcad последним перед этим местом, а предыдущие значения игнорируются (рис. 8).

Рис. 8. Пример двукратного определения переменной x

Если не установлено иное, Mathcad выводит на экран результаты вычислений с точностью до 0,001. Изменить количество выводимых десятичных знаков можно в меню Математика → Формат числа  → Выводимая точность. Данная установка не влияет на точность вычислений. Она затрагивает только вывод результата на экран и определяет количество цифр, отображаемых после десятичной точки. Например, число π при выводимой точности, равной 1, будет отображаться как 3.1, а при точности, равной 9, − как 3.141592654.

Если выводимую точность требуется изменить только для конкретного значения, то перед выполнением указанной выше операции следует поместить это значение в уголковый курсор.

Независимо от заданной точности вывода результата в системе Mathcad всегда поддерживается максимальная точность вычислений. При решении уравнений, вычислении интегралов и производных итерационными (приближенными) методами точность вычислений (погрешность численных расчетов) по умолчанию составляет 0,001. Чтобы установить другую точность вычислений, нужно задать требуемое значение для встроенной переменной TOL в меню Математика → Встроенные переменные → TOL или ввести его непосредственно в тексте документа, например, TOL:=0.000001, перед соответствующей формулой или в самом начале рабочего листа.

Прервать процесс вычислений можно, нажав клавишу Esc. Mathcad отметит выражение, вычисление которого было прервано, сообщением об ошибке «прервано». Для возобновления вычислений нужно нажать F9.

1.5. Лабораторная работа 1

Задание 1. Выполнить работу по образцу, представленному на рис. 9.

Задание 2. Вычислить значения функций при заданных значениях переменных в соответствии с вариантами табл. 3 и 4. При вычислении интеграла переменную интегрирования определить самостоятельно. Сравнить полученные результаты с табличными.

Рис. 9. Образец выполнения работы

Таблица 3

Арифметические выражения

Вариант	Исходные данные	Функция	Результат
1	2	3	4
1	x= 5;   a= 3,3		y = 0,539
2	x= 5;   a= 3,3		y = 0,27
3	x= 5;   a= 3,3		y = 0,371
4	x= 0,5;   a= 3,3		y = 2,814
5	x= 5;   a= 3,3		y = –46,72
6	x= 0,5;   a= 3,3		y = 82,443
7	x= 5;   a= 3,3		y = 1,22