Основы работы в автоматизированной системе Mathcad: Методические указания к выполнению лабораторных работ по информатике, страница 6

Окончание табл. 3

1	2	3	4
8	x = 5		y = –0,444
9	x = 0,5		y = –1,46
10	x= 0,5		y = 1,306
11	x= 0,5		y = –0,125
12	x= 0,5;   a= 3,3		y = 0,4
13	x= 0,5;   a= 3,3		y = 1,076
14	x= 0,5;   a= 3,3		y = –0,096
15	x= 0,5		y = 0,63
16	x= 0,5;   a= 3,3		y = 0,011

Таблица 4

Выражения с использованием операторов математического анализа

Вариант	Исходные данные	Функция	Результат	Функция	Результат
1	2	3	4	5	6
1	x = 15		b = –6,1		–0,34
2	a = 1,5		m = 15,57		–61,151
3	а = 5,8		p = 1754		0,232

Окончание табл. 4

1	2	3	4	5	6
4	u= 0,5		t = –2,36		50,657
5	x = 0,99		p = –691,1		–92,524
6	x = 0,57		t = 0,649		2,877
7	x = 6		d = 288,2		53,201
8	u = 45		d = 102,9		–2,887
9	x = p/20		s = –9,352		72,187
10	–		m = 63,47		33,108
11	–		f = 18,233		–0,359
12	j = 4		k = 84,5		1,056
13	y = 0,28		h = 1,231		9,105
14	x = 0,375		a = –26,42		602,312
15	t = p/3		v = –0,015		–6,042
16  1	x = 10		r = 2,083		3,503

2. ТАБУЛЯЦИЯ  ФУНКЦИЙ  И  ПОСТРОЕНИЕ  ГРАФИКОВ

2.1. Табуляция функции

Для получения таблицы значений функции задаются дискретные аргументы. В отличие от обычной переменной, имеющей только одно значение, дискретный аргумент представляет собой переменную, которая принимает ряд значений, отделяемых одинаковыми шагами, например, значения от 1 до 10 с шагом 1. Дискретные аргументы позволяют выполнять многократные вычисления или циклы с повторяющимися вычислениями. Дискретные аргументы еще называют ранжированными переменными.

Если дискретный аргумент определен, он принимает полный диапазон значений каждый раз, когда он используется. Если дискретный аргумент используется в выражении, Mathcad вычисляет выражение для каждого значения дискретного аргумента.

Дискретный аргумент задается следующим образом:

x := x_н ,  x_н + ∆x  ..  x_к ,

где     x – имя дискретного аргумента;

:= – символ присвоения значения;

          x_н – начальное значение дискретного аргумента;

          x_н + ∆x – следующее после начального значение аргумента (∆x – шаг изменения аргумента);

          x_к – конечное значение дискретного аргумента;

          .. – символ автоматического изменения (перебора) значений переменной от начального значения x_н до конечного x_к с шагом ∆x; этот символ вводится нажатием клавиши  ;  .

При записи значений дискретного аргумента шаг его изменения можно не выделять. В этом случае Mathcad определяет его автоматически. Если при записи дискретного аргумента следующее после начального значение опущено (т. е. шаг изменения аргумента не указан), то Mathcad принимает шаг изменения равным 1 или  –1 в зависимости от соотношения начального и конечного значений. Вывести на экран таблицу заданных значений дискретного аргумента можно обычным образом: набрать его имя и нажать символ «=». Примеры задания дискретного аргумента приведены на рис. 10.

Для получения таблицы значений функции нужно:

1)  задать диапазон изменения дискретного аргумента;

2)  записать выражение для расчета значений функции;

3)  вывести значения аргумента и функции.

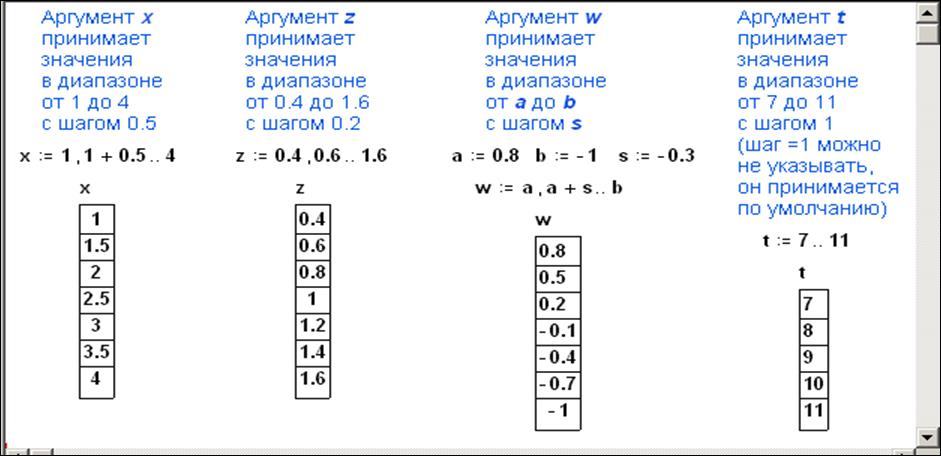
Рис. 10. Примеры задания дискретного аргумента

Если в математическом выражении используется дискретный аргумент, то при определении функции после ее имени в скобках обязательно должно быть указано имя аргумента, например, y(x). В противном случае Mathcad выдает ошибку «Нескалярная величина». На рис. 11 представлен пример расчета значений функции y(x) = sin(x) для значений x, изменяющихся на интервале [1; 3] с шагом ∆x = 0,5.