Розв’язання систем лінійних алгебраїчних рівнянь (СЛАР) за точними методами

Лабораторна робота  № 3

Розв’язання систем лінійних алгебраїчних рівнянь (СЛАР) за точними методами.

Мета роботи : Навчитися розв’язувати системи лінійних алгебраїчних рівнянь з застосуванням ЕОМ за точними методами.

Завдання  :

1. Скласти програму ЕОМ для розв’язання СЛАР за методом відповідно варіанту.

2.  Розв’язати дві СЛАР, матриця і праві частини яких розміщені у фалйі, що створюються програмами lr3_a.exe та lr3_b.exe  відповідно варіанту.

3. Оцінити похибку значень невідомих.

Метод розв’язання СЛАР :

 для парних варіантів -  зведення системи до трикутного вигляду за рекурентними  формулами;

для непарних варіантів - метод квадратного кореня;

для тих, що бажають і можуть - метод віддзеркалення.

Короткі теоретичні відомості

Системи лінійних алгебраїчних рівнянь (СЛАР)

Система з m лінійних алгебраїчних рівнянь з mневідомимиможе бути записана у наступному вигляді

,

де: - невідомі, значення яких треба знайти; - задані числові коефіцієнти при невідомих; - вільні члени (праві частини).

Розв’язком СЛАР звуть набір значень невідомих   , підстановка яких у рівняння системи перетворює їх одночасно на тотожності.

Для розробки схем розрахунків і програмування методів розв’язання СЛАР зручно використовувати матричні позначення, в яких система записується наступним чином.

,

де:  - матриця коефіцієнтів системи;

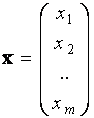 - вектор невідомих; 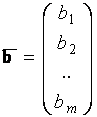  - вектор правих частин.

Метод послідовного виключення невідомих (Гаусса)

Цей метод є найбільш відомим і базується на простій і зрозумілій ідеї зведення системи еквівалентними перетвореннями до так званого трикутного вигляду, коли у перетвореній матриці системи всі коефіцієнти при невідомих нижче головної діагоналі дорівнюють нулю. Таким чином, починаючи з другого рівняння, кожне наступне містить на одне невідоме менше, а останнє є рівнянням з одним невідомим - і може бути просто розв’язане. Знайдене з останнього рівняння значення  можна підставити у попереднє рівняння і знайти з нього невідоме . І далі по черзі так званим зворотнім ходом визначити всі невідомі.