![]()
Розглянуті методи відносяться до класу точних, так як теоретично при відсутності похибки обчислень дають точний розв’язок системи за визначене число обчислень. У дійсності похибка обчислень має місце внаслідок округлення чисел при їх поданні в ЕОМ. Ця похибка зростає з ростом обсягу обчислень і для великих за розміром СЛАР може стати неприйнятною. Наступний метод розв’язання СЛАР має більшу у порівнянні з вже розглянутими стійкість до процесу зростання похибки обчислень
Метод віддзеркалення
Для
нормованого вектора ![]() (
(![]() )
матрицю
)
матрицю
![]() (де
(де ![]() -
одинична матриця відповідного розміру)
-
одинична матриця відповідного розміру)
звуть матрицею віддзеркалення внаслідок її властивості:
1) ![]()
тобто матриця є ортогональною.
2) ![]() тобто
тобто![]() євласним
вектором з власним числом
євласним
вектором з власним числом ![]() .
.
3) якщо ![]() (вектори ортогональні)
то
(вектори ортогональні)
то ![]() ,тобто
,тобто![]() є власним вектором з власним числом
є власним вектором з власним числом ![]() .
.
4) Будь-який вектор може бути розкладений по двом ортогональним векторам ![]() . Тоді
. Тоді ![]() ,
тобто вектор при множенні на матрицю
,
тобто вектор при множенні на матрицю ![]() ”віддзеркалюється”
відносно ортогональної до вектора
”віддзеркалюється”
відносно ортогональної до вектора ![]() площини.
площини.
Таким чином, щоб “віддзеркалити” вектор ![]() на певний напрям, визначений
одиничним вектором
на певний напрям, визначений
одиничним вектором ![]() , його можна помножити
зліва на матрицю віддзеркалення
, його можна помножити
зліва на матрицю віддзеркалення 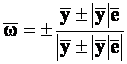
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.