Розв’язання систем лінійних алгебраїчних рівнянь (СЛАР) за точними методами, страница 2

Розроблено більш ефективні і зручні для програмування методи приведення СЛАР до трикутного вигляду. Нижче наведена схема Халецького () обчислення коефіцієнтів системи, зведеної до трикутного вигляду, за рекурентними формулами. Цей метод використовує подання матриці системи добутком двох трикутних матриць:

,

де - ліва трикутна,

 а  - права трикутна матриці.

Коефіцієнти цих матриць обчислюються за формулами:

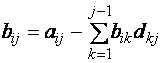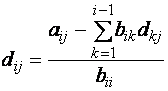при ;

при

для послідовності

Далі розв’язок системи може бути отримано послідовним розв’язанням двох трикутних систем:

   і    

Метод квадратного кореня

Цей метод можна вважати модифікацією схеми Халецького для випадку симетричної матриці системи.

Якщо матриця  є симетричною, тобто , її можна подати добутком матриць:

,

де: - права трикутна матриця;

 - діагональна матриця, діагональні елементи якої  дорівнюють +1 або –1.

Елементи матриць обчислюються за наступними формулами.

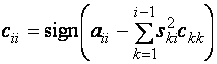
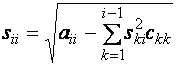
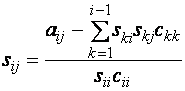
для

Далі розв’язок системи може бути отримано послідовним розв’язанням двох трикутних систем:

   і