Учет фактора времени при определении лагов капитальных вложений, страница 3

а) с вычислительной точки зрения формулы (3.46) и (3.47) не совсем удачны. Действительно, пусть строительство ведется равномерно в течение двух лет. Тогда очевидно, что применительно ко всей сумме капитальных вложений лаг равен одному году. Между тем по формуле (3.47) получается

Для устранения подобного рода искажений, вносимых концентрацией капитальных вложений в начале года, эти формулы полезно модифицировать:

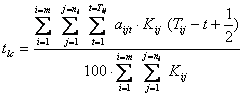                     (3.51)

и соответственно

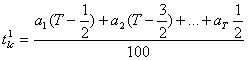.                     (3.52)

В случае когда распределение капитальных вложений задается не дискретно в процентах, а  непрерывной функцией времени

A_ij (t)( 0 ≤ t ≤ Т_ij  a_ij (t) dt = 1) расчет строительного лага для комплекса должен проводиться по формуле

t ^н_л 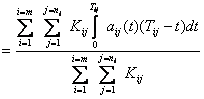.                                   (3.53)

б) нет четких указаний, в каких расчетах и как должны использоваться определяемые согласно (3.49), (3.53) значения строительного лага.

Представляется, что найденные согласно (3.49) — (3.50) величины t_лс пригодны лишь для расчетов общей (абсолютной) эффективности капитальных вложений. При расчетах ее для стоящих в знаменателе значений капитальных вложений в t-м году следует в числителе брать соответствующие К (t) значения эффектов (прироста национального дохода, прибыли) в год t + t_лс + t_ло (где t_ло — лаг освоения, величина которого может быть определена по формулам, близким по структуре приведенным выше).

Для расчетов же сравнительной эффективности капитальных вложений величина строительного лага должна определяться с учетом фактора времени, т. е. для дискретного случая

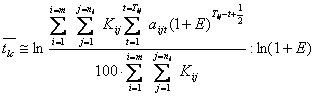.                         (3.54)

для  непрерывного случая

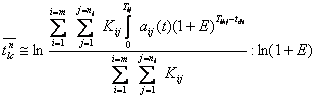.                   (3.55)

При этом в расчеты сравнительной эффективности капитальных вложений должна включаться величина сметной стоимости с учетом строительного лага, т.е. не К_ij , а К_ij (1+ Е) ^tлс . В случаях когда строительный лаг по вариантам существенно различается, такая корректировка капитальных вложений может оказаться заметной и повлиять на сравнительную эффективность оцениваемых решений.