Типы межатомных и межмолекулярных сил в твердых телах, страница 4

Значительные успехи достигнуты в последние десятилетия Коэном, Ашкрофтом, Харрисоном и другими исследователями за счет применения метода псевдопотенциала, изложение которого выходит за пределы нашего курса, но по которому уже имеется значительная литература. При этом широко используется применение в расчетных формулах эмпирических коэффициентов, определяемых опытным путем.

При определении энергии связи в металлах опираются на следующее основное предположение: на обобществленные электроны, находящиеся в объеме и обеспечивающие связь, действует поле, создаваемое ядрами и всеми другими электронами. Важную роль играют также кинетическая энергия электронов, энергия обменного взаимодействия валентных электронов с электронами, принадлежащими ионам остова и энергия корреляционного взаимодействия газа свободных электронов, учитывающая их спины. Так что в общем виде энергия связи металлических атомов в решетке полагается

U_с = - W + W_k – Ee – E_k,                                          (1.3.4)

где  энергия W включает в себя кулоновскую энергию Маделунга,  потенциальную энергию ионов и косвенное взаимодействие "ион-электрон-ион"; W_k - кинетическая энергия облака валентных электронов, Eе - энергия обменного взаимодействия и E_k - поправка на корреляционное взаимодействие электронов.

Громоздкие и сложные вычисления энергии сцепления атомов дают более или менее хорошее согласие теории с экспериментом пока лишь для простых металлов. Например, опираясь на метод псевдопотенциала, Ашкрофт и Лангрет рассчитали энергию связи для ряда металлов (см. табл. 3.4). Расчет велся по полученной авторами  формуле:

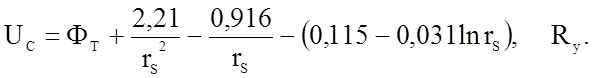          (1.3.5)

Здесь Ф_т соответствует W в формуле (1.3.4) и описывает ион-электрон-ион взаимодействие, включающее и энергию Маделунга, второй член представляет собой кинетическую энергию валентных электроновW_k, третий член - это обменная энергия Ее , последний член описывает энергию корреляционного взаимодействия электронов, r_s - среднее расстояние между валентными электронами, при расчетах используют величину r, подбираемую на основе измерений постоянной решетки а₀.

В формуле (1.3.5) при определении коэффициентов использовалась внесистемная единица измерения энергии "ридберг" (1Ry = 13,6 эВ).

Таблица 1.3.5

Энергия связи и сжимаемость металлов

Элемент	Отношение сжимаемостей К/К0*		Uc, ридберг/ электрон		DН0298
	Теория	Экспе- римент	Теория	Экспе- римент	кДж/моль	Эв/ атом
Al	1,41	1,38	3,5	3,9	314	3,34
Pb	1,55	1,79	3,2	3,5	196	2,04
Zn	1,10	1,05	2,1	2,1	130,9	1,35
Mg	0,86	0,89	2,1	1,9	147,4	1,53
Na	0,45	0,46	1,6	1,5	108	1,13
K	0,38	0,39	1,1	1,0	90	0,941

*K₀= 1,7×r_s⁵- сжимаемость свободных электронов; для определения энергии связи в единицах ридберг/ион, нужно умножить приведенную в табл. 1.3.5 величину U_c на валентность металла.

В табл. 1.3.5 приведены результаты численного расчета энергии связи для ряда металлов, здесь же приведены данные о сравнении теоретических и экспериментальных значений сжимаемости, часто применяемых для определения достоверности расчетов и получения необходимых параметров.

Таблица дополнена величиной DН⁰₂₉₈, теплотой сублимации, ближе всего соответствующей величине энергии связи. Для металлов она изменяется в пределах от 61,3 кДж/моль у ртути до 845,3 кДж/моль у вольфрама .

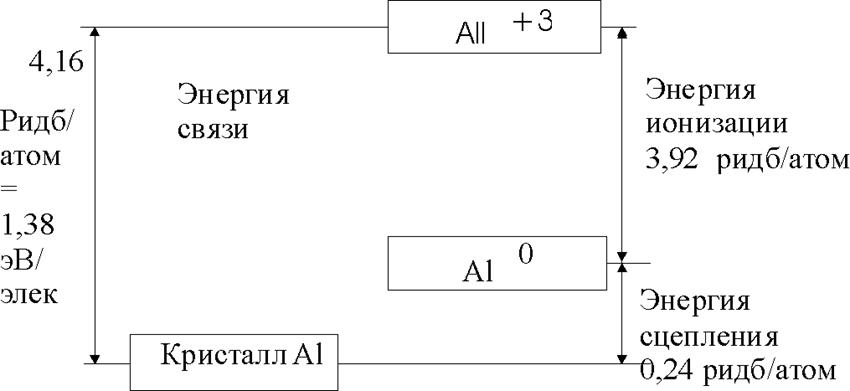
Очень часто при описании взаимодействия атомов в кристаллической решетке используют понятия "энергия связи", "энергия сцепления"  и "энергия ионизации". Связь между ними проиллюстрирована на рис.1.3.5 для атомов алюминия.

Рис. 1.3.5. Соотношение между энергиями связи кристалла, ионизации и сцепления атомов для алюминия

Расчет энергии связи для многообразия сплавов и элементов с примесями остается пока за пределами возможностей.

Поскольку металлическая связь не обладает направленностью, при образовании металлических кристаллов наблюдаются, как правило, эффекты максимально плотной упаковки. Координационное число К в первой сфере у 62 элементов составляет 8 или 12, у некоторых элементов (Ga, In, Tl), проявляющих металлические свойства, из-за недостатка валентных электронов межатомные связи имеют смешанный характер и структура резко отличается от обычных металлов.

Полуметаллические атомы As, Bi, Sb  образуют гофрированные сложные структуры с координационным числом 3 в пределах слоя, причем расстояние между атомами внутри слоя всегда меньше, чем между атомами, находящимися в соседних слоях.

1.3.4. Водородная связь

Этот тип связи очень важен, так как именно он обеспечивает межмолекулярную связь воды в жидком и кристаллическом состояниях. Вода является необходимым компонентом всех биологических систем и при формировании в природе многих минералов. При производстве керамики, огнеупоров, строительных материалов и конструкций многие особенности технологии как раз определяются применением воды, ее воздействием на сырье и промежуточные материалы. Наконец, стойкость изделий в условиях взаимодействия с влагой атмосферы, растворение и коллоидообразование таких веществ, как соли, глины, известь определяются особыми свойствами воды.