Элементы зонной теории электронного строения твердых тел

1.4. ЭЛЕМЕНТЫ ЗОННОЙ ТЕОРИИ ЭЛЕКТРОННОГО СТРОЕНИЯ ТВЕРДЫХ TЕЛ

В комплексе свойств твердых тел (электро- и теплопроводность, теплоемкость, оптические и магнитные свойства), определяющую роль играет не только ионный остов решетки, но и энергетическое состояние электронов внешних оболочек атомов, объединенных в кристалл или аморфный конгломерат. Нужно отдавать себе отчет в том, что попытки точных расчетов поведения отдельных электронов бессмысленны. Квантово-механический принцип неопределенностей запрещает попытки вычисления точных траекторий или орбит электронов уже в отдельных атомах и молекулах. Поскольку макроскопическое тело массой 1 г содержит около 1023 атомов, то следовало бы ожидать, что и трудность задачи возрастет во столько же раз в сравнении с задачами для отдельных молекул. Однако в действительности это не так и, как это ни удивительно, многие решения для кристаллических структур являются даже более простыми и точными, чем для сложных молекул. Причина этого лежит в периодичности кристаллической структуры и, следовательно, силовых полей, воздействующих на электроны, ионы, заряженные дефекты, а также в достаточной протяженности структуры, зачастую позволяющей рассматривать ее как бесконечно протяженную.

Известная модель свободных электронов в металлах, наряду с качественно верными ответами об электро- и теплопроводности, о термоэлектронной эмиссии, о некоторых контактных и термоэлектрических явлениях, - оказывается совершенно бессильной при описании свойств полупроводников и диэлектриков, и зачастую не может дать ответ на некоторые вопросы о важнейших свойствах: почему у различных твердых тел при близких параметрах прочности, пластичности, плотности столь поразительно могут отличаться электрические свойства - удельное электросопротивление колеблется от »10¹⁴ Ом×м у хороших диэлектриков до »10^-8 Ом×м у проводников? Почему у тех же веществ так мало отличается теплоемкость? Почему столь различно изменяется с температурой электропроводность у металлов и полупроводников? Почему у некоторых веществ при низких температурах проявляется сверхпроводимость?

Очень продуктивной во многих отношениях оказалась зонная теория электронного строения твердых тел.

1.4.1. Происхождение электронных энергетических зон

Строгие аналитические решения даже для одного  электрона в поле более чем двух силовых центров-ядер или ионов - до сих пор не получены в силу больших математических трудностей. Приближенные решения, достигнутые довольно сложными методами теории возмущений, дали некоторые важные ответы о деталях поведения электронов в молекулах. Здесь мы проведем качественное обсуждение ожидаемого возможного существования и расположения энергетических электронных уровней. Принципы и пути, используемые при точных решениях, будут рассмотрены в п.4.2.

1.4.1.1. Дискретные энергетические уровни свободных атомов

Известно, что в изолированных атомах состояние всех электронов однозначно описывается четырьмя квантовыми числами: n - главным, l - орбитальным, m - магнитным и s  - спиновым. Главное квантовое число n  характеризуется целочисленными значениями  n = = 1,2,3,..., для невозбужденных атомов, определяет номер и энергию стационарного состояния атома. В частности, в простейшем атоме водорода набор разрешенных энергетических уровней (термов) определяется соотношением

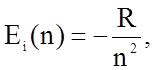                                                                        (1.4.1)

где  R = 13,6 эВ- универсальная постоянная Ридберга, n = 1,2,3,...,.

В изолированном атоме водорода занятым оказывается лишь одно состояние из этого набора;  состояния, соответствующие дробным значениям n, запрещены.

Орбитальное квантовое число l принимает значения l=0,1,2,3,..., (n - 1) - всего  n  значений - и определяет механический орбитальный момент количества движения (момент импульса) электрона  . Величина момента импульса   в состоянии, характеризуемом значением квантового  числа l, может быть найдена из соотношения

                                                                      (1.4.2)

где 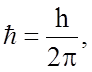  h = 6,62×10^-34 Дж×с - постоянная Планка.

Магнитное квантовое число m принимает целочисленные значения из ряда m_l = -l,-l+1,...,-1, 0, 1,..., l-2, l-1, l   и определяет ориентацию вектора орбитального момента  относительно направления в пространстве, выделенного внешним магнитным полем . Вектор _e может ориентироваться относительно направления  лишь так (рис. 1.4.1), что его проекция подчиняется соотношению

                                                                            (1.4.3)

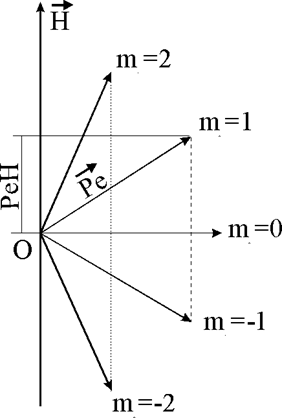Рис.1.4.1. Возможные ориентации вектора орбитального момента электрона относительно напряженности внешнего магнитного поля Н

Всего при данном значении l возможно (2 l + 1) значений  m_l (и ориентаций вектора ).

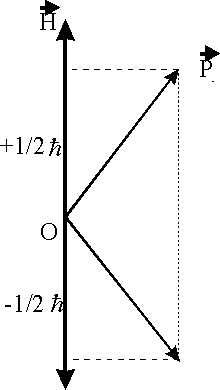Спиновое квантовое число s может принимать лишь два значения (s = +1/2 или s = -1/2) и определяет ориентацию относительно того же направления собственного (или спинового) момента количества движения   электрона.

Рис.1.4.2. Возможные значения спина относительно направления, выделенного Н

Как видно из рис.1.4.2, возможны лишь два варианта ориентации   относительно , при этом величина проекции составляет

                                                                                (1.4.4)

Состояния электронов, у которых орбитальное квантовое число l=0, называются s - состояниями. В каждом атоме число s – состояний определяется числом n , поэтому соответствующие состояния и электроны называют 1s , 2s , 3s  и т.д. состояниями (электронами). Состояния и электроны с l = 1 называют  р-состояниями и электронами, l = 2 называют d - состояниями и электронами. Далее используются индексы f , g  и  h .

В многоэлектронных атомах формула 1.4.1 не применима, так как возможные значения энергии зависят не только от главного квантового числа n , но и от орбитального l: Е = Е( n , l), причем n и l принимают взаимосвязанные дискретные целочисленные значения, что соответствует возможным наборам дискретных значений энергии Е(n,l). Например, при n = 1, т.е. Е=Е(1,0) (К-оболочка), возможны лишь значения l = 0, m_l= 0, s = ± 1/2 - всего возможно максимум одно 1s - энергетическое состояние с двумя 1s - электронами.

При n = 2 возможны значения: Е(1,0), т.е. n = 1, l = 0, m_l = 0 и  s = ±1/2 - одно 1s-состояние с двумя 1s -электронами; Е(2,0), т.е. n == 2, l = 0, m_l = 0 и  s = ±1/2 - одно 2s-состояние с двумя  2s -электронами;  Е(2,1),  т.е. n = 2, l = 1,  m_l = -1,0,1 и s = ±1/2 - всего три 2р -состояния с шестью 2р-электронами на них.

Рис. 1.4.3. Энергетические уровни и их заполнение в невозбужденном изолированном атоме Na (условный масштаб по оси энергий)

Всего у атомов с n = 2 возможны 5 значений энергии - два различных s - состояния и три р-состояния (последние - с одинаковым значением энергии). Все уровни s принято называть невырожденными, т.к. каждому из них соответствует единственное энергетическое состояние электрона в атоме, в котором, в соответствии с принципом Паули, могут находиться максимум два электрона с различными спинами. Все остальные уровни - р, d, f и т.д. называют вырожденными, так как каждому из них отвечает не одно, а несколько разрешенных электронных состояний. В частности, уровни р вырождены трехкратно, так как им соответствуют 3 возможных энергетически равноправных состояния, отличающихся значениями магнитного квантового числа m_l (при l = 1,  m_l = -1,0, +1). Уровни d имеют пятикратное вырождение ( m_l = -2, -1,0,1,2) и для их максимального заполнения требуется 10 электронов.