Элементы зонной теории электронного строения твердых тел, страница 5

Волновой вектор , входящий в (1.4.21), входит и в функцию Блоха. Движение электрона в силовом поле решетки отличается от движения в свободном пространстве модуляцией значения потенциальной энергии, что учитывается введением в качестве амплитуды Y - функции  или в одномерном случае U(х). Соответствующим образом периодически будет изменяться и плотность вероятности координаты Y×Y^* (см. рис.1.4.11). Равновероятны состояния, представленные точками A и А₁, B и B₁ и т.д., то есть у электрона в решетке имеются наборы физически эквивалентных состояний.

Математически это представляется в виде периодических функций волнового вектора (или квазиимпульса ) величины энергии и волновой функции Y. Часто рассматривают изменения  или  в  - пространстве или  - пространстве.

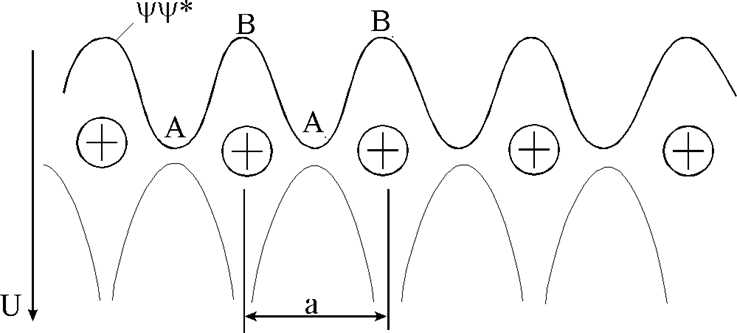Рис. 1.4.11.  Энергия электрона в периодической структуре

Области значений волнового вектора , в пределах которых энергия электрона , являющаяся периодической функцией, испытывает полный цикл своего изменения, называются зонами Бриллюэна.

Для одномерного цепочечного кристалла, изображенного на рис.1.4.11, первая зона Бриллюэна простирается от -p/а до +p/а, занимая зону 2p/а. Вообще зона Бриллюэна в общем случае представляет собой многогранник, построенный в  - пространстве вокруг точки  = 0. Все неэквивалентные значения компонентов вектора  (и, следовательно, энергии) в простой кубической решетке ограничены интервалами

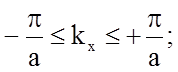
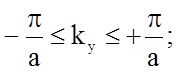
                 (1.4.22)

Теоретически доказано, что вектор  из зон Бриллюэна с большими номерами сводится к первой зоне (эквивалентность физических состояний) и поэтому она считается основной.

Доказано, что для полного описания всей совокупности физических состояний электрона в кристалле достаточно рассматривать только область значений , ограниченную первой зоной Бриллюэна. Совокупность всех энергетических уровней электрона, описываемых функцией  и называют энергетической зоной (n - имеет фиксированное значение номера зоны). Подобно тому, как атомы расположены периодически в обычном трехмерном пространстве координат, энергетические зоны оказываются периодическими в пространстве импульсов.

Нетрудно убедится, что интервал 2p/a   представляет собой период обратной решетки кристалла (см. п.1.5.2), причем сомножитель 2p отражает периодичность функций Cos  и  Sin, входящих в тригонометрическую форму записи  волновой Y- функции. Понятие зон Бриллюэна широко используется в физике твердого тела и далеко не ограничивается лишь пояснением энергетического спектра электронов.

1.4.2.4. Энергетический спектр электронов в кристалле

Энергетический спектр электрона в кристалле может быть определен, если в уравнении (1.4.13) точно определен вид периодического решеточного потенциала . Собственные значения функции Блоха и энергии  существенно зависят от этого потенциала. Но точный вид V (г) определить практически невозможно. Приходится использовать некоторые приближения. Наиболее часто применяются следующие методы расчета энергетического спектра:

- самосогласованный расчет с использованием известных атомных констант (чаще всего это метод ортогонализированных плоских волн);

- эмпирические методы, где для  наилучшего согласования теории и эксперимента применяются данные экспериментов (метод псевдопотенциала);

- подбор для описания потенциала функций специального вида, удовлетворяющих физическому смыслу задачи (методы функций Грина, присоединенных плоских волн), метод линейных комбинаций атомных орбиталей (JIKAO).

Точные аналитические решения при этом не получены, для определения возможных значений  используют быстродействующие ЭВМ и на этом пути достигнут значительный прогресс. Показано, что в простейшем случае одномерной решетки энергетические состояния электрона представляют собой набор зон разрешенных и запрещенных значений (рис.1.4.12). Учитывая возможность сведения возможных значений  к значениям первой зоны Бриллюэна, часто представляют график лишь для первой зоны 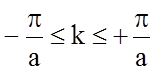   (не заштрихованная часть рис.1.4.12).

Видно, что в пределах разрешенных зон график функции  близок к графику, описывающему состояние свободного электрона, но на границах зон Бриллюэна при 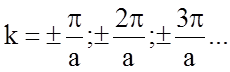   наблюдается разрыв Е при переходе из одной зоны в другую. Физическую природу этих разрывов можно понять, проанализировав значения в  точках разрыва на границе с зоны с номером n. С одной стороны 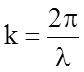, с другой стороны 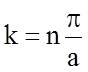, или                            

 2а = nl.                                                                              (1.4.23)

          Если записать уравнение Вульфа-Брегга для дифракции 2a×sinj = nl, то видно, что уравнение (1.4.23) описывает дифракцию электронных волн при условии их нормального падения на атомные плоскости. Очевидно, при этих условиях функция Блоха (1.4.17) описывает уже не бегущую, а стоячую волну, так как электрон с таким волновым вектором испытывает в  реальной решетке брэгговское отражение, т.е. не может существовать в решетке с данной величиной  параметра "а".

          В заключение отметим, что в трехмерном случае картина может значительно усложниться вследствие различий в значениях трехмерного потенциала  в разных направлениях решетки. Тогда и зависимость  в трехмерном кристалле может иметь различия для разных направлений в зоне Бриллюэна, форма которой также зависит от типа кристаллической решетки. Важным следствием этого  может быть перекрытие разрешенных зон в разных направлениях  (в одномерном  случае перекрытие разрешенных зон невозможно), а также совпадение зон, запрещенных в одном направлении, с разрешенными относительно других направлений. Вообще в трехмерном кристалле количество разрешенных энергетических состояний возрастает в сравнении с одномерным.

 Говорить о создании сколько-нибудь надежных теорий электронного строения аморфных твердых тел пока преждевременно. Наука находится на стадии накопления экспериментального материала о возможных энергетических состояниях электронов.

Однако не слишком существенное различие в виде зависимости  для свободных электронов в кристаллах (если пренебречь разрывами в пунктирном параболическом графике рис.1.4.12) позволяет утверждать, что общая концепция энергетических зон пригодна и в этом случае, однако точные детали строения зон во многих случаях еще предстоит изучить.