Элементы зонной теории электронного строения твердых тел, страница 4

Следующее упрощение следует из резкого различия масс ядер и электронов, приводящего к резким различиям в характере их движения.

Ядра в кристаллах и аморфных телах подавляющее по протяженности время находятся в колебательном движении около положений равновесия с небольшими скоростями. Легкие электроны совершают вращательное движение около ядер (электроны внутренних оболочек) и поступательное движение в межъядерном пространстве (обобществленные и валентные электроны). В силу инерционности ядра не успевают следовать за движением каждого электрона, и их движение определяется усредненным полем сил ближних частиц (адиабатическое приближение).

Рассмотрение решетки как конгломерата, состоящего из неподвижных ионов, создающих некоторое силовое поле, в котором независимо  движутся электроны, позволяет свести многоэлектронную задачу к одноэлектронной. Используется метод Хартри-Фока, основной идеей которого служит замена суммарной потенциальной энергии U в уравнении Шредингера выражением вида 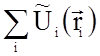, представляющим собой энергию взаимодействия i-го электрона с некоторым эффективным полем, характеризующим действие всех остальных электронов на данный электрон. Это приближение заметно упрощает вычислительную процедуру, при этом, однако, требуются дополнительные меры по учету принципа Паули.

Эффективное поле  называют самосогласованным, так как оно должно учитывать влияние собственного поля i-го электрона  на поле кристалла; кроме того, чтобы найти , надо знать волновые функции электронов Y_i(r_i), которые, в свою очередь, можно найти, если  известно. Для нахождения таких решений используют вариационные методы, требующие  решений систем интегро-дифференциальных уравнений Хартри-Фока, что зачастую чрезвычайно сложно.

Если взять потенциальную энергию электрона в кристалле в виде суммы

,                                                             (1.4.13)

где  описывают долю, вносимую эффективным самосогласованным полем электронов; а  - долю, вносимую взаимодействием с ядрами, то можно записать уравнение Шредингера для одночастичной  задачи в виде

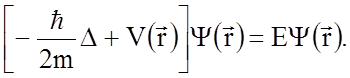                                           (1.4.14)

Здесь член - 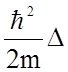 описывает кинетическую энергию частицы,

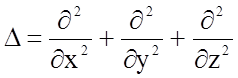 - оператор Лапласа.

1.4.2.2. Функции Блоха

Точный вид потенциала , как правило, неизвестен, но оказалось, что для получения достаточно фундаментальных теоретических результатов можно и не знать его точного вида, достаточно лишь быть уверенным, что  является периодической функцией координат, причем пространственный период совпадает, естественно, с периодом изучаемой кристаллической решетки.             

Замена в уравнении (1.4.13) энергии  на  , где  (n₁, n₂, n₃) - произвольные целые числа, а  - векторы единичных трансляций решетки, приводит к решению, где функция  будет иметь вид

и является периодической функцией с периодом решетки, то есть

В этом случае решениями уравнения (1.4.14) являются функции Блоха, представляющие собой волновые функции, описывающие плоские волны, модулированные функцией с периодичностью решетки:

                                                             (1.4.15)

где  - некоторая периодическая функция с периодом, равным периоду изучаемой  решетки, зависящая еще и от волнового вектора электрона (напомним, что 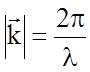, где l - длина волны де Бройля). В конденсированном теле волновой вектор  играет роль аналога всего  набора квантовых чисел (n, l,m,s), описывающих состояние электрона в атоме.

1.4.2.3.   - вектор,  - пространство, зоны Бриллюэна

При описании одномерного движения свободного электрона вдоль оси Х уравнение Шредингера имеет простой вид:

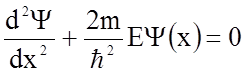,                                                         (1.4.16)

причем 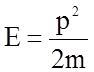  представляет собой только кинетическую энергию при нерелятивистском движении, т.к. U= 0 (свободное движение),  р - импульс электрона.

Решением уравнения (4.16) в этом случае является Y - функция, описывающая бегущую волну

                                                                         (1.4.17)

где А - амплитуда волны.

Согласно формуле де Бройля импульс электрона р, его длина волны l и модуль его волнового вектора k  связаны соотношением

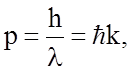                                                                          (1.4.18)

где 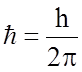, а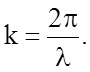 

Вектор , совпадающий с направлением распространения электронной волны, таким образом, может использоваться при описании энергии электрона. В случае свободного электрона его кинетическая энергия равна         

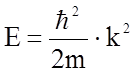                                                                          (1.4.19)

и носит параболический квадратичный характер (рис.1.4.10,а).

Уравнение (1.4.19) описывает энергетическую дисперсию свободного электрона.

Поскольку величина w = Y×Y^* (где  - комплексно сопряженная функция в данном случае) представляет плотность вероятности обнаружения частицы в точке с координатой х, то, как следует из уравнения (1.4.17), эта вероятность для свободного электрона от значения координаты не зависит

    (1.4.20)

Поскольку подобное решение можно провести для любой координаты, это значит, что все точки пространства для свободного электрона эквивалентны (рис.1.4.10,6).

Так как в кристаллической решетке или аморфном твердом теле электроны внешних атомных оболочек находятся в условиях влияния сильных полей соседних атомов, в уравнении Шредингера (1.4.11) существенную роль играют как кинетическая, так и потенциальная энергии.

Силовое поле, в котором движется электрон в правильной одномерной кристаллической решетке, в первом приближении можно представить в виде периодической разрывной функции (рис.1.4.11, также рис.1.4.4) с периодичностью "а" решетки.

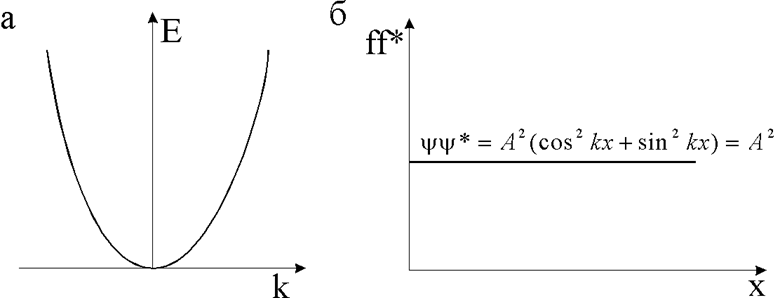Рис. 1.4.10. Энергия свободного электрона

Следовательно, и энергия взаимодействия электрона в кристалле должна быть некоторой периодической функцией, изменяясь со временем для движущегося электрона. Вместо импульса свободного электрона введена характеристика

,                                                                                 (1.4.21)

которую называют квазиимпульсом электрона.