Элементы зонной теории электронного строения твердых тел, страница 3

Введение примесей в чистые вещества приводит к  изменению строения энергетических зон. Наиболее часто это выражается в появлении отдельных дополнительных уровней в запрещенной зоне, а также в изменениях в плотности заселения уровней разрешенных зон.

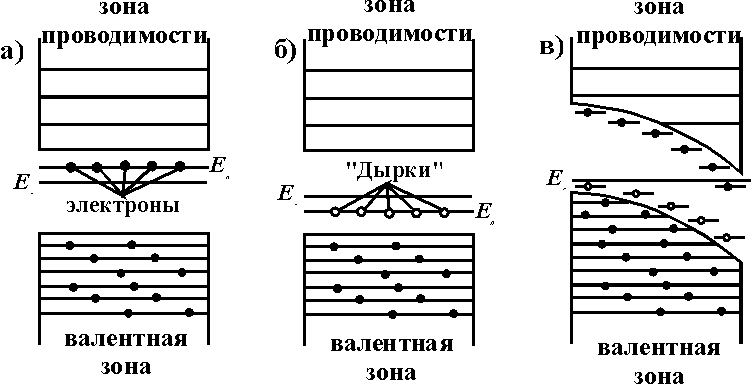
Рис. 1.4.7. Зонное строение полупроводниковых кристаллов (при Т= 0К) с донорной примесью (а), с акцепторной примесью (б), диэлектриков с примесями или аморфной структурой (в).

Искажение и ослабление межатомных связей вследствие аморфизации кристаллической структуры с точки зрения распределения электронов по энергиям также может быть представлено как появление в запрещенной зоне некоторого количества дополнительных энергетических уровней или изменения заселенности электронами разрешенных уровней. При этом электронные уровни, располагающиеся вблизи дна зоны проводимости, называются донорными, а уровни вблизи вершины валентной зоны – акцепторными (рис.1.4.7).

На положение уровней энергии Е_V и Е_C, соответствующих границам запрещенной зоны, а  также на вероятность заполнения энергетических уровней электронами решающим образом влияет температура.

Обратите внимание на положения уровня Ферми, с ростом температуры он стремится к положению в середине запрещенной зоны

1.4.1.3. Распределение электронов по энергетическим состояниям

В соответствии с представлениями квантовой механики вероятность f(E_i) заполнения электроном уровня с энергией Е_i в зоне проводимости определяется из функции Ферми, справедливой для любых частиц с полуцелым спином:

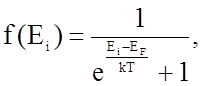                                                                  (1.4.5)

где k  - постоянная Больцмана, Т - абсолютная температура, Е_F - энергия Ферми, e - основание натурального логарифма.

          При Т = 0К все уровни Е_i от уровня Ферми Е_F и ниже заняты электронами с вероятностью f(Е_i) = 1. С повышением температуры электроны подвергаются тепловому возбуждению и, в силу близости подуровней в разрешенной зоне, легко занимают уровни с Е_i >Е_F, однако это относится лишь к электронам с уровней, ближних к уровню Ферми (расположенных в зоне шириной kT, прилежащей к уровню Е_F).

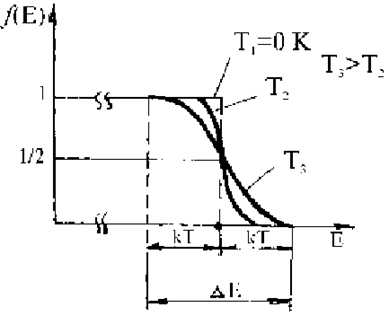
Рис.1.4.8. График распределения Ферми по уравнению (1.4.5): T₃ > T₂: DE = 2kТ =  0,1 эВ при Т = =1000 К; т.к. например, Е_F = 3,1 эВ (Na), E_F = 7,l эВ (Cu), то DЕ << Е_F,

Вероятность занятости уровня Е_F остается постоянно равной ½  (рис.1.4.8), для уровней Е_i < Е_F вероятность f(Е_i) > 1/2, а для Е_i > Е_F - f(E_i) < 1/2.

Разрешенные состояния внутри энергетической зоны распределены неравномерно. Число состояний N(Е)  в интервале значений энергии (Е+dЕ) при абсолютном нуле в твердом  теле объемом V определяется функцией распределения Ферми-Дирак

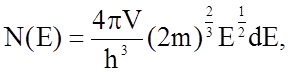                                                     (1.4.6)

где h - постоянная Планка, a m - эффективная масса электрона, в металлах мало отличающаяся от массы покоя (но лишь в металлах!).

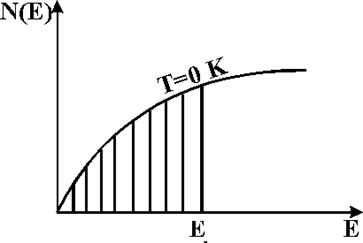Рис.1.4.9.  График функции   распределения  Ферми-Дирака  для электронов    при Т = 0К

График функции распределения N(Е) представлен на рис.1.4.9. Если проинтегрировать выражение (1.4.6) в пределах от 0 до Е_F, то получим

                                                           

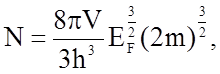
откуда уже легко определить энергию  Ферми  E_F:

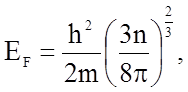                                                                      (1.4.7)

если найти экспериментально n = N/V - концентрацию электронного газа.

Знание величины энергии Ферми Е_F позволяет вычислить среднюю энергию электронов при абсолютном нуле по формуле

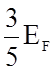=                                                                                 (1.4.8)

и максимальную V_max  и среднеквадратичную скорости движения электронов в металлах при абсолютном нуле:

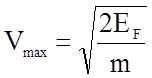      и 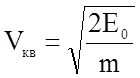  .                                         (1.4.9)

Количественные отличия распределения электронов по энергиям от распределения, свойственного металлам, при 0К можно оценить из соотношения

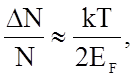                                                                            (1.4.10)

где 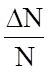 - доля электронов, располагающаяся в зоне kT, прилегающей к уровню Ферми E_F . Например, для меди Е_F = 7,1 эВ, тогда  при Т = 300К 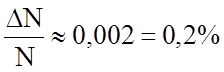; остальные 99,8% электронов находятся на более низких энергетических уровнях и в тепловых движениях не могут принять участие. Эта оценка будет нам необходима при анализе теплоемкости различных тел.

1.4.2. Теоретические принципы зонной модели электронного строения твердых тел

1.4.2.1. Уравнение Шредингера

Выше уже отмечалось, что точные решения для квантовомеханических систем с числом частиц более трех не получены. Точное описание состояния микрочастиц, объединенных в структуру твердого тела - ядер и электронов - в принципе может быть достигнуто, если удастся решить соответствующее квантово-механическое уравнение Шредингера. Стационарные состояния описываются уравнением

                                                                       (1.4.11)

где  - оператор Гамильтона, представляющий собой сумму операторов  кинетической энергии и - потенциальной энергии. Оператор   в свою очередь состоит из сумм энергий отдельных ядер и всех электронов. Потенциальная энергия системы зарядов должна учитывать как силы притяжения, так и силы отталкивания между всеми частицами системы: отталкивание в системах "ядро-ядро", "электрон-электрон", притяжение в системах "ядро-электрон",  причем в принципе каждая из частиц взаимодействует со всеми остальными частицами системы. Е - собственное значение энергии или энергия твердого тела.

Волновая функция Y, входящая в обе части уравнения (1.4.11), зависит от координат всех частиц системы

                                            (1.4.12)

где  - радиус-векторы электронов, общим числом N,

 - радиус-векторы ядер, число которых составляет n.

Из-за огромного числа независимых переменных уравнение (1.4.11) в общем виде в настоящее время не может быть решено. Однако введение некоторых ограничений, вытекающих из физического смысла и экспериментальных данных, позволяет получить полезные приближения. Так, ограничивая волновую функцию  физически разумными требованиями конечности, однозначности и непрерывности, получаем, что уравнение Шредингера (1.4.11) удовлетворяется не при любых значениях собственной энергии Е, а только при некоторых. Это позволяет сделать вывод о квантуемости энергии движения частиц в твердом теле.