Элементы зонной теории электронного строения твердых тел, страница 6

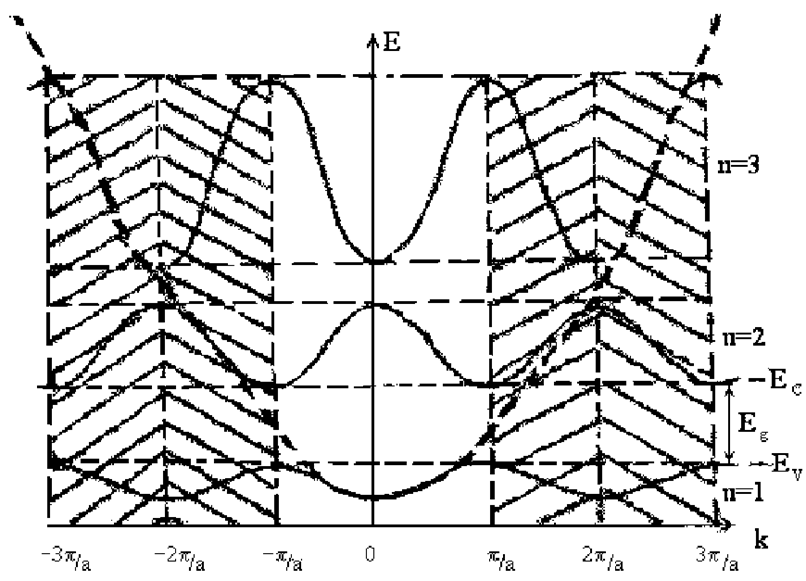
          Из общих квантовомеханических представлений следует, что в аморфной структуре состояния с заданными значениями квазиимпульса электронов нестационарны, и, следовательно, теряет смысл введение понятия зон Бриллюэна, однако сохраняет смысл такое важное понятие, как плотность состояний в зонах N (Е) и функция распределения Ферми-Дирака.

Рис.1.4.12. Энергия электрона в решетке с периодом “a”.

Рис.1.4.13. Зависимость плотности состояний N (Е) энергии электронов в кристалле (а) и аморфных телах (б,в,г). Локализованные состояния заштрихованы

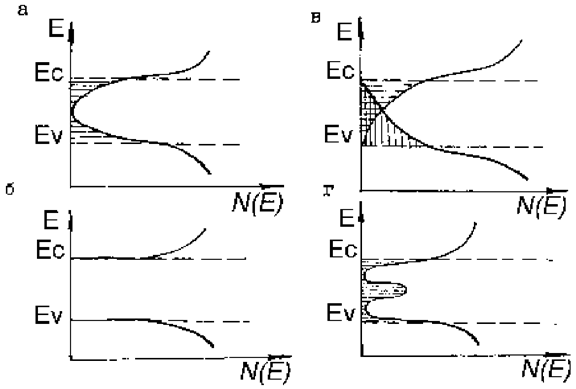Очень большую роль в энергетическом распределении в некристаллических веществах играют локализованные состояния, обусловленные как флуктуациями плотности, так и наличием примесных атомов и дефектов типа оборванных связей. На рис. 1.4.13 схематически представлены зависимости плотности состояний для разных типов некристаллических твердых веществ (б,в,г) и для сравнения - для кристалла (а).

Возможно как существование точной нижней границы спектра разрешенных флуктуационных состояний (б), так и ее отсутствие (в). Наличие локализованных состояний, связанных с множественными дефектами структуры обозначается обычно пиком (рис.4.13,г), расположенным в середине запрещенной зоны, уровень Ферми Е_F находится в ее центре.

1.4.2.5. Эффективная  масса частицы, движущейся в кристалле

К понятию "эффективная масса частицы" мы уже обращались.

При анализе движения электронов и "дырок" в кристаллах широко используется понятие "эффективная масса" соответствующего носителя заряда. Ознакомимся с его физическим смыслом.

На свободный электрон, находящийся в электрическом поле напряженностью , действует сила  = e.Под действием этой силы он  приобретает ускорение  

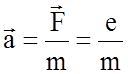
 ,                                                                     (1.4.24)

где m - масса электрона, причем m = m₀ - массе покоя при скорости  v<<c (скорости света).

В периодическом поле решетки, кроме внешнего поля напряженностью, на движение влияет еще и потенциал внутреннего поля, поэтому характер движения электрона усложняется. Оно описывается с помощью волнового пакета, составленного из блоховских функций (1.4.17). Групповая скорость частицы связана с  энергией Е выражением

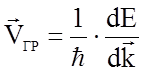  .                                                                     (1.4.25)

Учтем, что квазиимпульс электрона , тогда , а выражение (1.4.25) приобретет вид 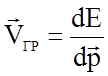. Определим ускорение  электрона      

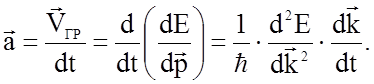                                       (1.4.26)

Под действием поля  на электрон действует сила , которой за время dt  над электроном будет совершена работа

                                           (1.4.27)

Но 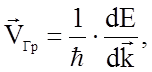   поэтому   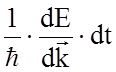. Эта работа идет на приращение энергии dЕ, состоящей из кинетической  E_K и потенциальной U части

dE=

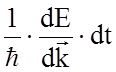
откуда получаем

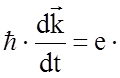
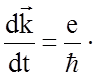
=      или                                       (1.4.28)

Подставляя значение (1.4.28) в (1.4.26) для ускорения, получаем

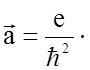
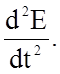=                                                                 (1.4.29)

 Если теперь записать второй закон Ньютона 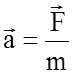   и подставить , то видно, что уравнение (1.4.29) представляет собой уравнение движения электрона в кристалле, если величине

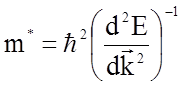                                                                   (1.4.30)

присвоить смысл массы (получаем уравнение ). Поскольку величина m^* является лишь коэффициентом в уравнении Ньютона и не отражает ни гравитационные, ни инерционные свойства частицы в общепринятом смысле, то она называется эффективной массой. Еще точнее ее можно было бы назвать "квазимассой". Такая величина введена не только для электрона (она обозначается m_n^*), но и для дырок" ( m_p^*) - физических объектов, вообще не имеющих массы покоя.

Эффективная масса отражает меру взаимодействия частицы с кристаллической решеткой, применительно к электрону m_n^* может быть как больше массы покоя m₀, так и меньше. Более того, она может быть отрицательной. Нетривиальность в поведении электронов особенно проявляется на границах зон Бриллюэна.

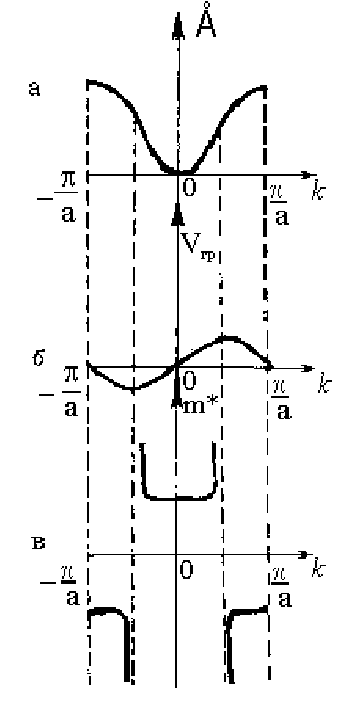Рис. 1.4.14. Зависимость от волнового числа энергии (а), групповой скорости (б) и эффективной массы

Графическая зависимость m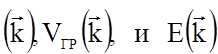^*  схематически представлена на рис.1.4.14  и интерпретируется следующим образом.       При движении электрона под действием внешней силы F часть работы этой силы переходит в кинетическую энергию электрона Е_K, а часть - в потенциальную U, поэтому скорость электрона и его кинетическая энергия возрастают медленнее, чем у свободного электрона, т.е. приближаясь к середине зоны, он становится как бы тяжелее, чем покоящийся электрон (m_n^*>m₀). Если теперь в потенциальную энергию системы электрон - решетка будет переходить не только работа внешней силы, но и часть кинетической энергии, уже запасенной электроном, то движение электрона будет замедляться () и он будет себя вести как частица с отрицательной массой. Это наблюдается при приближении электрона к потенциальному барьеру, то есть к вершине разрешенной зоны, при условии отражения.

Разрыв в графике m_n^*(k) означает, что в центре зоны понятие m^* потеряет смысл и им можно пользоваться лишь в практически наиболее важных случаях описания поведения электронов и дырок вблизи дна и вершины энергетической зоны. Однако в кристаллах реализуется и обратный случай, когда в кинетическую энергию электрона переходит не только работа внешней силы, но и часть потенциальной энергии системы. В этом случае электрон ускоряется быстрее, чем частица с массой m₀, т.е. он становится как бы легче (m_n^*<m₀).

У дна зоны (вблизи  k = 0) масса примерно постоянна и равна массе покоя (m_n^*=m₀). Масса "дырок" m_p характеризует степень сопротивления сил межатомной связи перестройке под действием внешних сил.

Введение эффективной массы - один из вариантов (простейший, быть может) учета "несвободности" электрона в решетке. Переменность эффективной массы в пределах зоны Бриллюэна означает изменчивость связи электрона с остовом в различных пространственных его  положениях.