Цифровые фильтры с конечной импульсной характеристикой: Методические рекомендации по выполнению лабораторной работы

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ  УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

Дисциплина  «Теория  и  обработка  сигналов»,     6-й семестр

ЛАБОРАТОРНАЯ  РАБОТА  № 11

ЦИФРОВЫЕ ФИЛЬТРЫ

С  КОНЕЧНОЙ  ИМПУЛЬСНОЙ  ХАРАКТЕРИСТИКОЙ

Цель работы:изучение методов анализа и синтеза фильтров с конечной импульсной характеристикой (КИХ – фильтры,  другое название – нерекурсивные фильтры) с использованием сглаживающих оконных функций.

Задание и порядок выполнения работы.

1.  Ознакомьтесь с теоретическими сведениями по построению, анализу и синтезу КИХ – фильтров на основе метода взвешивания, изложенными в  Приложениях 1 и  2, а также в [1, стр. 80 - 92].

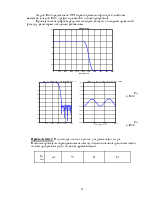
2.  Постройте в одном графическом окне (используйте subplot) графики импульсной характеристики КИХ - фильтра нижних частот с прямоугольным окном, нормированной  частотой среза  рад/отсч.  для двух значений  длины фильтра  N = 14  и   N = 50. Для оформления графиков введите необходимые заголовки и метки. Прокомментируйте поведение характеристик.

3.  Используя функцию DTFT (Приложение 4),  вычислите преобразование  Фурье  импульсных характеристик из п.2 и постройте графики их АЧХ в линейном масштабе (одно графическое окно) и в децибелах (20*log₁₀(H(e^jω) – другое окно) для 512 отсчетов частоты.  Для более наглядного представления нормируйте значения АЧХ на её максимальное значение (max(H(e^jω))).
По характеристикам в линейном масштабе определите полосу пропускания, переходную полосу и полосу задерживания фильтра с обязательным указанием единиц измерения.   Поясните, как влияет порядок фильтра на ширину переходной полосы и уровень пульсаций АЧХ в полосах пропускания и задерживания. Чем объясняются эти пульсации?

4.  С помощью функции load() загрузите в рабочее пространство Matlab файл speech.mat. Используя операцию свертки, выполните фильтрацию  звукового сигнала  nspeech2  каждым из двух фильтров.
          С помощью функции sound() прослушайте исходный сигнал  и сигналы после фильтрации. Прокомментируйте результаты прослушивания. Оказала ли фильтрация заметное влияние на качество звучания?
         Примечание. Для регулировки уровня звука можно использовать синтаксис sound(M*var_name), где M – специфицированная константа,  var_name - имя переменной.

5.  Постройте в одном графическом окне графики прямоугольного окна и окон Хэмминга, Ханна, Блэкмана  для N = 25. Используйте для этого команды Matlab   hamming, hanning, blackman.   Введите необходимые заголовки и метки графиков.

6.  Используя функцию DTFT() с 512 частотными отсчетами, вычислите ДВПФ оконных функций из предыдущего пункта и постройте в одном окне графики амплитудных спектров в шкале децибел.
 7.      Определите ширину главного лепестка и относительный уровень боковых лепестков в децибелах (относительно амплитуды главного лепестка). Для более точного измерения используйте команды zoom и axis. Составьте таблицу с измеренными и соответствующими теоретическими значениями величин (таблица П.1) и их разностями. Прокомментируйте результаты. Обратите внимание, что  подобным подходом можно  достаточно точно измерять неизвестные параметры  окон.

8.  Постройте графики окон Кайзера  и их амплитудных спектров для        N = 25,  β = 0, β = 1 и  β = 5. Используйте для этого функцию Matlab  kaiser(N, beta) и функцию DTFT() с 512 отсчетами частот. Определите ширину главного лепестка и относительный уровень боковых лепестков  для каждого случая. Прокомментируйте, как значение параметра β влияет на форму окна и уровень боковых лепестков.

9.  Проведите расчет (синтез) фильтра по индивидуальному заданию (Приложение 3). Постройте в заключение расчета график АЧХ спроектированного фильтра и проверьте её  соответствие заданию.

10.  Выполните фильтрацию звукового сигнала  nspeech2  спроектированным фильтром и оцените качество звучания сигнала до и после фильтрации.

11.  Используя функцию b=fir1(n, Wn, window)   рассчитайте КИХ –фильтр со спецификацией  и типом окна из п. 9.  С помощью функции fvtool(b)  выведите АЧХ этого фильтра и сопоставьте результаты расчета фильтров в п. 9 и п.11.

12.    Составьте отчет по лабораторной работе. В отчете должны быть представлены

титульный лист,

название и цель работы,

формулировки пунктов работы, необходимые формулы и выражения,   m – файлы,   графики, комментарии, выводы по синтезу КИХ – фильтров с использованием сглаживающих оконных функций.

Литература

1.  Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. пособие.- Новосибирск. Изд-во НГТУ,  1998 - ч.2.

2.  Сергиенко А.Б.  Цифровая обработка сигналов. СПб.: Питер, 2003.

Web – источники

1.  http://web.mit.edu/6.555/www/fir.html

2.  http://www.filter-solutions.com/FIR.html

Контрольные вопросы и упражнения

1.  Сформулируйте определение КИХ – фильтра, запишите и объясните его общее уравнение. Какие преимущества и недостатки свойственны этим фильтрам?

2.  Изобразите графически спецификации следующих фильтров:
а)  ФНЧ с допустимым уровнем пульсаций 0,1 в полосе пропускания   и ослаблением не менее 30 дБ в полосе задерживания   ;
б)   ФВЧ с максимально допустимым уровнем пульсаций 0,05 в полосе пропускания    и затуханием не менее 40 дБ в полосе задерживания  .

3.  Фильтр 1-го порядка имеет уравнение  .  Объясните характер операции фильтрации. Запишите передаточную функцию, определите АЧХ и ФЧХ фильтра и постройте их графики.

4.  Для КИХ –фильтра с уравнением 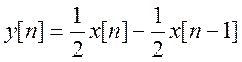 получите передаточную функцию, АЧХ и ФЧХ. К какому типу фильтров следует его отнести?

5.  Сформулируйте понятие идеального ФНЧ. Запишите выражение импульсной характеристики фильтра. Почему такой фильтр нельзя реализовать практически? Как можно приближенно реализовать требования идеального ФНЧ?  Какой характер ФЧХ будет иметь такой фильтр?

6.  Объясните принцип синтеза КИХ – фильтров на основе сглаживающих оконных функций.

7.  Перечислите и объясните особенности основных оконных функций (прямоугольного окна,  окон Хэмминга, Ханна и Блэкмана).

8.  Почему фильтры на базе оконных функций имеют пульсации АЧХ в полосе пропускания и полосе задерживания? Как обеспечить допустимый уровень пульсаций ?

9.  В среде Matlab постройте графики окон Ханна, Хэмминга, Блэкмана и их АЧХ.

10.  Как изменяется АЧХ окна Хэмминга с изменением размера окна?  Как влияет размер окна на ширину переходной полосы фильтра?

11.  Перечислите и объясните основные параметры оконных функций.

12.  Запишите выражение окна Кайзера. Какие особенности имеет это окно?

13.  В среде Matlab постройте графики окна Кайзера его логарифмическую АЧХ для .

14.  Сформулируйте методику проектирования КИХ –фильтра на базе взвешивающих оконных функций.

15.  Спроектируйте КИХ -фильтр нижних частот, удовлетворяющий следующим требованиям: . Постройте график АЧХ спроектированного фильтра и  убедитесь, что он удовлетворяет исходным требованиям.

Приложение 1. КИХ – фильтры на основе  взвешивающих оконных функций.

          1.  В соответствии с названием КИХ – фильтры имеют импульсную характеристику с конечным числом ненулевых коэффициентов. Уравнение выход – вход такого фильтра

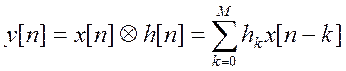                                                 (1)

где x[n] –вход,  y[n] - выход, h[n]- импульсная характеристика,  M -  порядок фильтра.

Преимущества КИХ – фильтров:

- такие фильтры всегда устойчивы,

- при соответствующем порядке можно обеспечить необходимые требования к  АЧХ фильтра,

- достаточно просто получить линейную ФЧХ.

Основной недостаток: большой объем вычислений при высоком порядке М. Для повышения быстродействия в таких случаях используют вычисление свертки в частотной области.

Можно доказать, что для обеспечения линейности фазовой характеристики необходимо, чтобы ИХ фильтра была симметрична относительно её середины, т.е. 

                                                                                                                   (2)

2. Частотная характеристика идеального дискретного КИХ – фильтра нижних частот может быть записана в виде

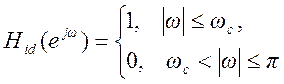                                                            (3)

где ω_с – угловая частота среза.

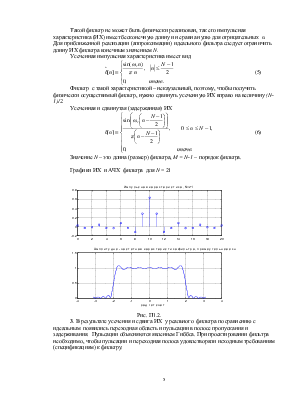
Импульсная характеристика идеального фильтра 

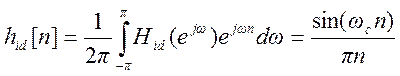  .                                                 (4)

Графики

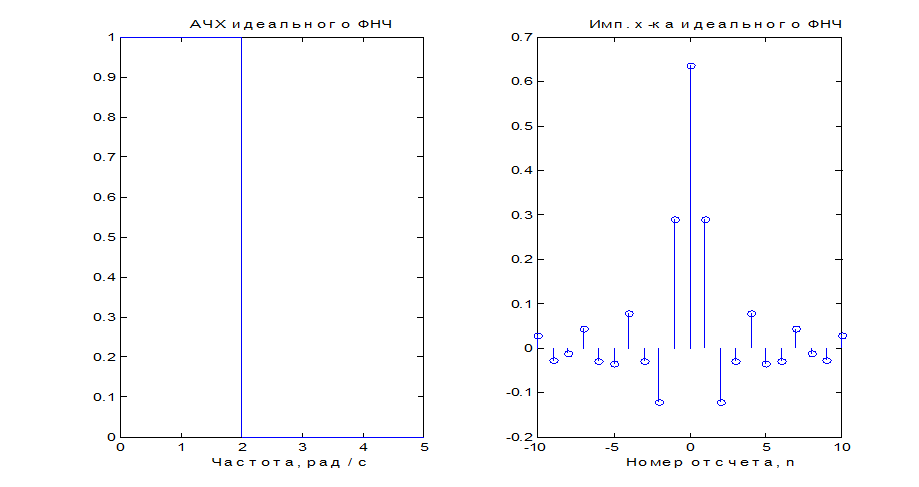
                                                           Рис. П.1.

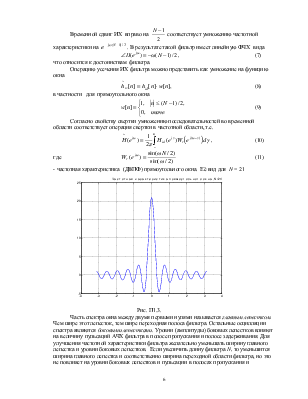
Такой фильтр не может быть физически реализован, так его импульсная характеристика (ИХ) имеет бесконечную длину и не равна нулю для отрицательных  n. Для приближенной реализации (аппроксимации) идеального фильтра следует ограничить длину ИХ фильтра конечным значением N.