Цифровые фильтры с конечной импульсной характеристикой: Методические рекомендации по выполнению лабораторной работы, страница 2

Усеченная импульсная характеристика имеет вид

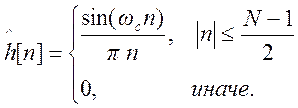                                                         (5)

Фильтр  с такой характеристикой – некаузальный, поэтому, чтобы получить физически осуществимый фильтр, нужно сдвинуть усеченную ИХ вправо на величину (N-1)/2.

Усеченная и сдвинутая (задержанная) ИХ

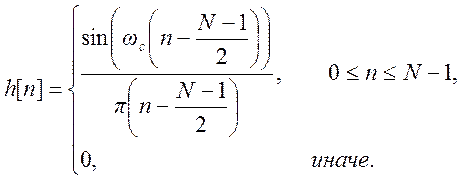                              (6)

Значение N – это длина (размер) фильтра, M = N-1 – порядок фильтра.

Графики ИХ  и АЧХ  фильтра  для N = 21

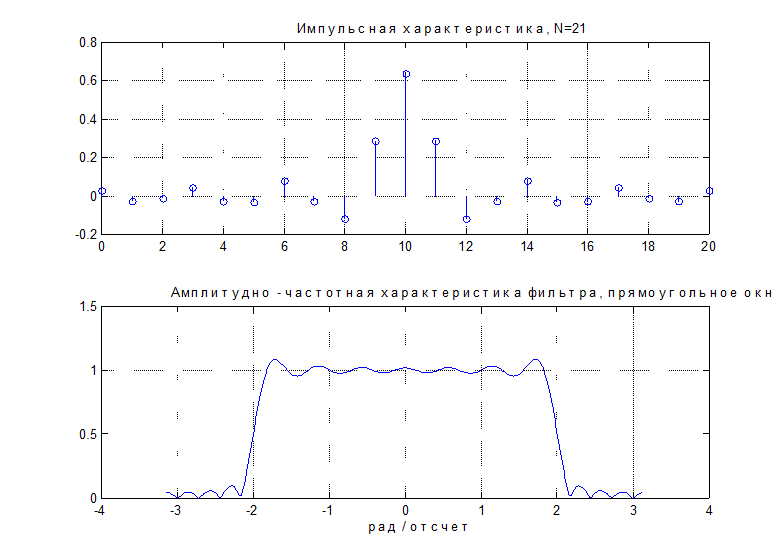
                                                                       Рис. П1.2.

3. В результате усечения и сдвига ИХ  у реального  фильтра по сравнению с идеальным  появились переходная область и пульсации в полосе пропускания и задерживания.  Пульсации объясняются явлением Гиббса. При проектировании фильтра необходимо, чтобы пульсации и переходная полоса удовлетворяли исходным требованиям (спецификациям) к фильтру.

Временной сдвиг ИХ  вправо на 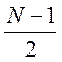  соответствует умножению частотной характеристики на . В результате такой фильтр имеет линейную ФЧХ  вида    

,                                                      (7)

что относится к достоинствам  фильтра.

            Операцию усечения ИХ фильтра можно представить как умножение на функцию окна

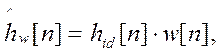                                                          (8)

в частности   для  прямоугольного окна

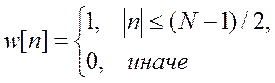                                                 (9)

Согласно свойству свертки умножению последовательностей во временной области соответствует операция свертки в частотной области, т.е.

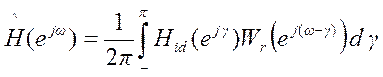,                  (10)

где 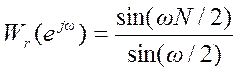                                                                                                (11)

- частотная характеристика  (ДВПФ) прямоугольного окна.  Её вид для  N = 21

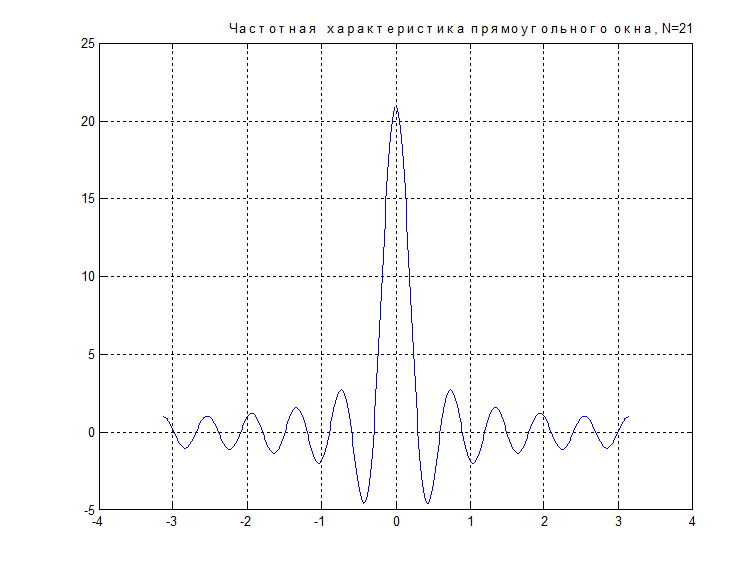
                                Рис. П1.3.

Часть спектра окна между двумя первыми нулями называется главным лепестком. Чем шире этот лепесток, тем шире переходная полоса фильтра. Остальные осцилляции спектра являются боковыми лепестками. Уровни (амплитуды) боковых лепестков влияют на величину пульсаций АЧХ фильтра в полосе пропускания и полосе задерживания. Для улучшения частотной характеристики фильтра желательно уменьшать ширину главного лепестка и уровни боковых лепестков.  Если увеличить длину фильтра N, то уменьшится  ширина главного лепестка и соответственно ширина переходной области фильтра, но это  не повлияет на уровни боковых лепестков и пульсации в полосах пропускания и задерживания из-за явления Гиббса.  Размер (длина) окна – единственный управляемый параметр прямоугольного окна, но как уже отмечалось, он не влияет на уровни боковых лепестков.

4. Для улучшения характеристик фильтра используют другие оконные функции (окна), которые спадают к нулю более плавно, чем прямоугольное окно.  Известно несколько десятков таких оконных функций. Наиболее популярными из них являются

а)  прямоугольное окно

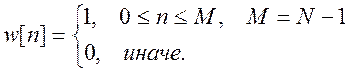                                                 (12)

б)  окно Ханна

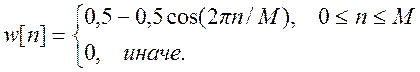                                     (13)

в)  окно Хэмминга

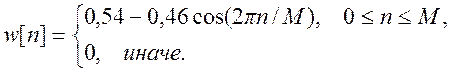                    (14)

г)  окно  Блэкмана

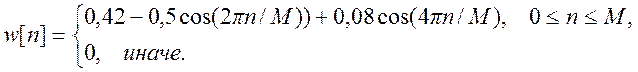            (15)

Чем более гладкой является форма окна, тем меньше амплитуда боковых лепестков, но тем шире главный лепесток окна и, значит, переходная полоса фильтра.

Вид  окна Хэмминга и его амплитудного спектра для  N= 21

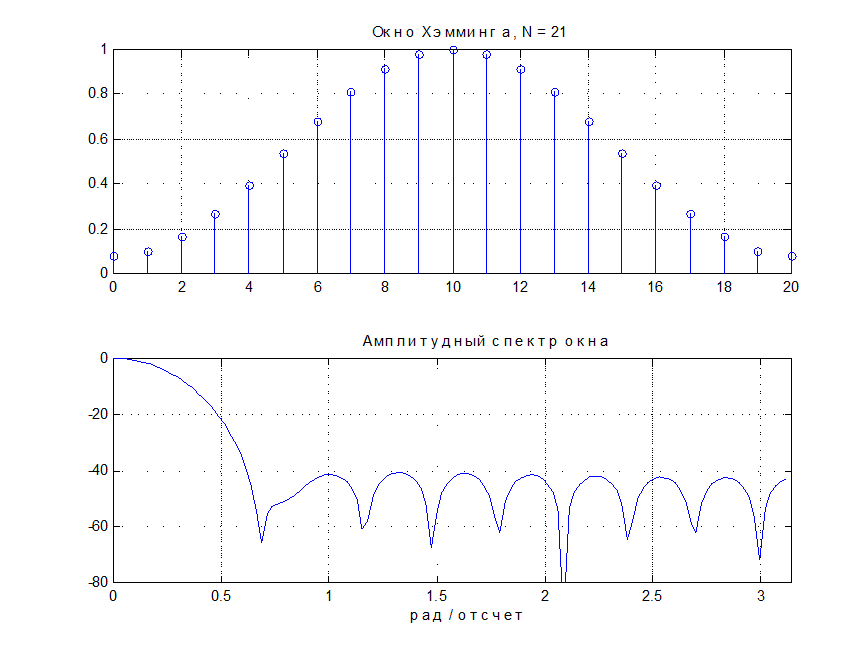
                                                      Рис. П1.4.

            Основные параметры четырех перечисленных выше окон, используемые при проектировании фильтров,  приведены в таблице П1.

Таблица  П.1

Тип  окна	Ширина  главного  лепестка	Относительный  уровень  боковых лепестков в дБ	Уровень пульсаций в полосах пропускания и задерживания,   дБ
Прямоугольное Ханна Хэмминга Блэкмана	4π / M 8π / M 8π / M 12π / M	-13 -31 -41 -57	-21 -44 -53 -74

5.   Для перечисленных выше окон единственным управляемым параметром является размер окна. Но относительные уровни боковых лепестков и, значит, пульсации (отклонения) в полосах пропускания и задерживания  у таких окон не зависят от  длины окна.

Более гибкие возможности предоставляет так называемое окно Кайзера.  Функция, описывающая его поведение

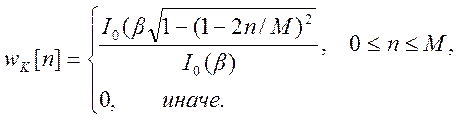                   (16)

Здесь   - модифицированная функция Бесселя первого рода нулевого порядка (в Matlab – это функция  besseli()),

            М  - порядок фильтра, позволяющий управлять шириной переходной области фильтра,

             - параметр формы окна, с помощью которого можно регулировать амплитуду боковых лепестков и форму окна.

            Выражения для расчета параметров фильтра с окном Кайзера:

 - допустимый уровень пульсаций в полосах пропускания и задерживания,

 ,                                                                                                          (17)

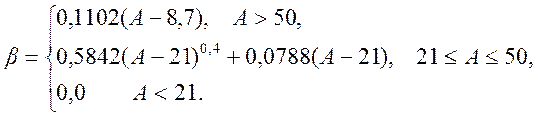                                         (18)

порядок фильтра

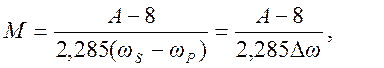                                                                   (19)

Δω  - ширина переходной полосы.

Приложение  2. Пример проектирования  КИХ – фильтра нижних частот

          График спецификации   фильтра

-  переходная  полоса

           

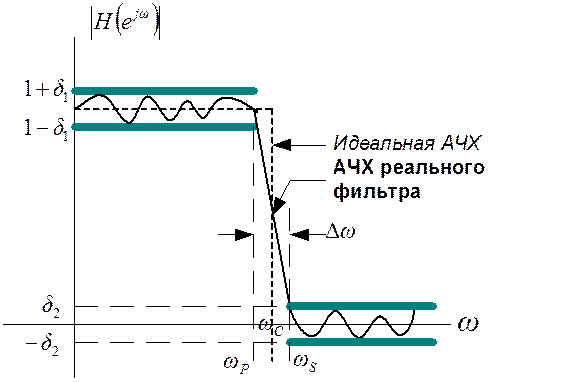
                                                         Рис.  П.2.1

             - граничная частота полосы пропускания,

             - граничная частота полосы задерживания, 

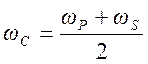 - частота  среза  фильтра,

 - допустимый уровень отклонений (пульсаций) АЧХ в полосе пропускания,

- допустимый уровень отклонений (пульсаций) АЧХ в полосе задерживания.

Пусть заданы следующие исходные требования к фильтру:

·  ,

·   Гц,

·     Гц.
Проектирование фильтра заключается в выборе типа окна, определении порядка и коэффициентов (значений ИХ) уравнения фильтра.

1.  Выберем частоту дискретизации (отсчетов)  в соответствии с требованиями теоремы отсчетов равной 10000 Гц, при этом частота Найквиста  равна 5000 Гц. Нормированные граничные частоты полосы пропускания и полосы задерживания окажутся  равными  0,25 Гц/отсчет и 0,35 Гц/отсчет соответственно. Частота среза фильтра 
 Гц/отсчет, соответственно   Ширина переходной полосы фильтра  Гц, нормированная угловая переходная полоса  .

2.  Определим допустимый уровень пульсаций   как  или в децибелах  . Такому уровню ошибки аппроксимации идеальной АЧХ  фильтра соответствует окно Хэмминга, для которого  A = 53 дБ  (см. таблицу П1).  Поэтому для дальнейшей реализации фильтра выбираем окно Хэмминга.

3.  Определяем порядок фильтра с окном Хэмминга по выражению (таблица П1)

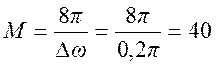
4.  Окно Хэмминга фильтра
 

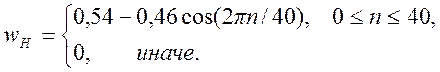
5.  Импульсная характеристика рассчитанного фильтра

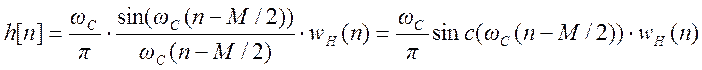
На рис. П2.2 представлена АЧХ спроектированного фильтра в линейном масштабе, а на рис. П2.3 –график пульсаций в  полосе пропускания.

Приведенные на графиках результаты свидетельствуют, что спроектированный фильтр удовлетворяет исходным требованиям.

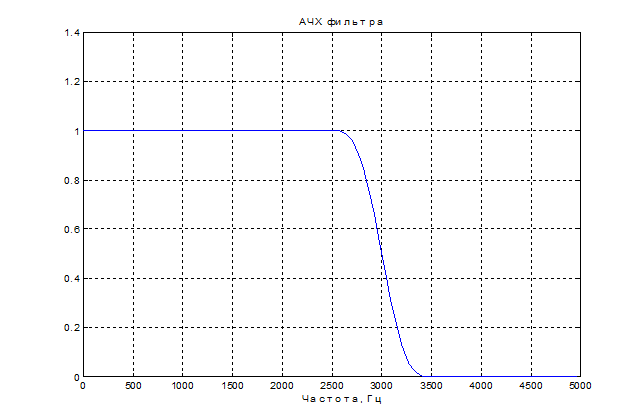
                                         Рис. П2.2

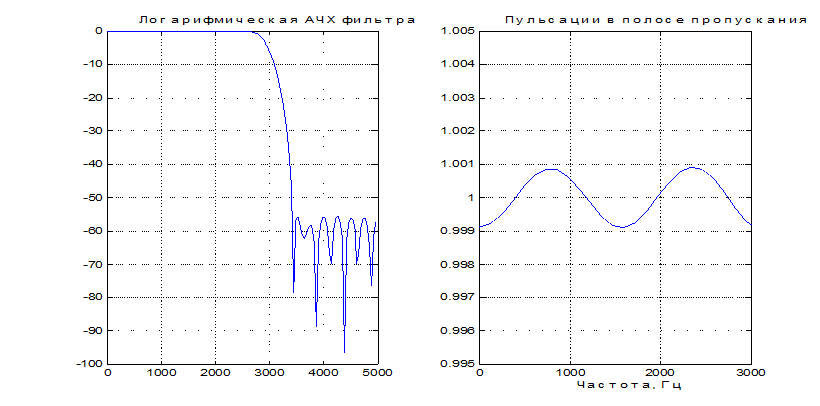
                                                             Рис. П2.3.                                                                 

Приложение 3. Индивидуальные задания для расчета фильтра

В таблице приведены нормированные на частоту отсчетов значения граничных частот полосы пропускания (ω_P) и полосы задерживания(ω_S).

№ п/п	ωP	ωS	δ1	δ2
1 2 3 4 5 6 7 8 9 10 11 12	0,4π 0,45π 0,6π 0,5π 0,3π 0,4π 0,6π 0,45π 0,55π 0,6π 0,7π 0,55π	0,6π 0,55π 0,8π 0,6π 0,5π 0,55π 0,7π 0,6π 0,75π 0,7π 0,8π 0,65π	0,02 0,004 0,001 0,005 0,01 0,002 0,008 0,01 0,001 0,001 0,005 0,004	0,01 0,008 0,002 0,006 0,01 0,001 0,008 0,01 0,002 0,002 0,005 0,003

Приложение 4.   Файл – функция вычисления ДВПФ

function [X,w] = DTFT(x,M)

% Функция вычисляет значения DTFT от вектора x.

% Обращение

%             [X,w] = DTFT(x,0)

% здесь X - вектор значений DTFT,

% w - вектор угловых частот.

% Если желательно вычислить DTFT с M значениями частоты,

% используется обращение

%             [X,w] = DTFT(x,M)

% Этот вариант используется, когда размер вектора x 

% меньше  размера вектора частот w,

% при этом x дополняется нулевыми значениями

N = max(M,length(x));

% Приведение FFT к размеру 2^m

N = 2^(ceil(log(N)/log(2)))

% Вычисление  fft

X = fft(x,N);

% Вектор  частот

w = 2*pi*( (0:(N-1))/N );

w = w - 2*pi*(w>=pi)

% Сдвиг FFT к интервалу от -pi до +pi

X = fftshift(X);

w = fftshift(w);