НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 10
ЦИФРОВЫЕ ФИЛЬТРЫ
С КОНЕЧНОЙ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКОЙ
Группа: АТ-33
Вариант: 1 Преподаватель:
Студент: Шадрина А.В. доц. Щетинин Ю.И.
2006
Цель работы: изучение методов анализа и синтеза фильтров с конечной импульсной характеристикой с использованием сглаживающих оконных функций.
Выполнение работы:
1.
Графики импульсной характеристики КИХ-фильтра нижних частот с
прямоугольным окном частотой среза ![]() для значений
длины фильтра
для значений
длины фильтра ![]() и
и ![]() .
.
Импульсная характеристика идеального дискретного КИХ-фильтра
имеет бесконечную длину и не равна нулю для отрицательных значений ![]() :
:
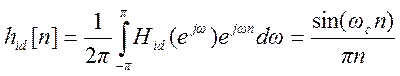 .
.
Для того чтобы получить физически
осуществимый фильтр, следует ограничить импульсную характеристику конечным
числом ![]() , а затем сдвинуть усеченную
характеристику вправо на величину
, а затем сдвинуть усеченную
характеристику вправо на величину 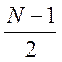 .
.
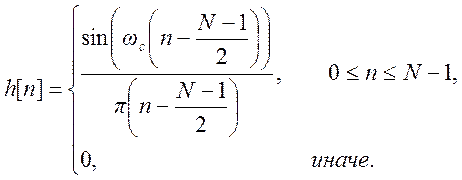
Значение ![]() –
это длина (размер) фильтра,
–
это длина (размер) фильтра, ![]() – порядок
фильтра.
– порядок
фильтра.
Matlab Script (labrab101.m)
N = input('Введите длину фильтра N = ');
wc = 2;
n = 0:N-1;
h = sin(wc.*(n-(N-1)/2))./(pi.*(n-(N-1)/2));
stem(n,h)
xlabel('Номер отсчёта, n')
ylabel('h[n]')
>> subplot(2,1,1)
>> labrab101
Введите длину фильтра N = 15
>> title('Импульсная характеристика КИХ-фильтра для N=15')
>> subplot(2,1,2)
>> labrab101
Введите длину фильтра N = 50
>> title('Импульсная характеристика КИХ-фильтра для N=50')
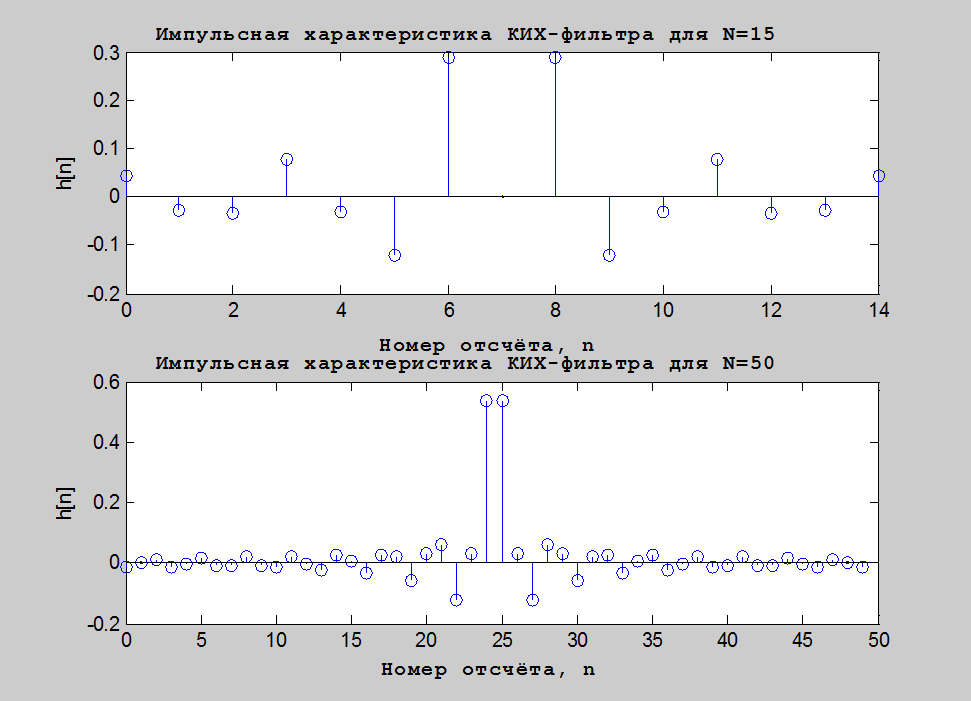
Рис.1. Графики
импульсной характеристики КИХ-фильтра нижних частот с прямоугольным окном
частотой среза ![]() для значений длины
фильтра
для значений длины
фильтра ![]() и
и ![]()
Комментарий: Если
рассматривать частотную характеристику цифрового фильтра как ряд Фурье: 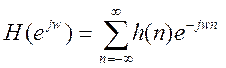 , то коэффициенты этого ряда
, то коэффициенты этого ряда ![]() будут представлять собой значения
импульсной характеристики фильтра. В данном случае было проведено усечение ряда
Фурье в первом случае до
будут представлять собой значения
импульсной характеристики фильтра. В данном случае было проведено усечение ряда
Фурье в первом случае до ![]() , а во втором – до
, а во втором – до
![]() , а затем усеченные характеристики
были сдвинуты по оси отсчётов вправо на
, а затем усеченные характеристики
были сдвинуты по оси отсчётов вправо на 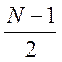 для
получения каузального фильтра. При
для
получения каузального фильтра. При ![]() ширина главного
лепестка составляет 2, а при
ширина главного
лепестка составляет 2, а при ![]() - 1, т.е. при
увеличении длины фильтра главный лепесток импульсной характеристики сужается.
Если же рассматривать уровень боковых лепестков (с помощью
- 1, т.е. при
увеличении длины фильтра главный лепесток импульсной характеристики сужается.
Если же рассматривать уровень боковых лепестков (с помощью ![]() ), то при увеличении
), то при увеличении ![]() он увеличился по абсолютной величине
с
он увеличился по абсолютной величине
с ![]() до
до ![]() .
Таким образом, можно сделать вывод, что при использовании аппроксимации
идеальной АЧХ фильтра прямоугольным окном нельзя одновременно сузить главный
лепесток (и тем самым уменьшить переходную область) и уменьшить уровни боковых
лепестков (уменьшить пульсации в полосах пропускания и задерживания фильтра).
Единственным управляемым параметром прямоугольного окна является его размер, с
помощью которого можно влиять на ширину главного лепестка, однако же, на
боковые лепестки он особого влияния не оказывает.
.
Таким образом, можно сделать вывод, что при использовании аппроксимации
идеальной АЧХ фильтра прямоугольным окном нельзя одновременно сузить главный
лепесток (и тем самым уменьшить переходную область) и уменьшить уровни боковых
лепестков (уменьшить пульсации в полосах пропускания и задерживания фильтра).
Единственным управляемым параметром прямоугольного окна является его размер, с
помощью которого можно влиять на ширину главного лепестка, однако же, на
боковые лепестки он особого влияния не оказывает.
2.
Вычисление ДВПФ импульсных характеристик из п.1 с помощью функции
![]() . Графики их АЧХ в линейном масштабе
и в децибелах для 512 отсчетов частоты. Полоса пропускания, переходная
полоса и полоса задерживания фильтра. Влияние порядка фильтра на ширину
переходной полосы и уровень пульсаций АЧХ в полосах пропускания и задерживания.
. Графики их АЧХ в линейном масштабе
и в децибелах для 512 отсчетов частоты. Полоса пропускания, переходная
полоса и полоса задерживания фильтра. Влияние порядка фильтра на ширину
переходной полосы и уровень пульсаций АЧХ в полосах пропускания и задерживания.
Matlab Function (DTFT.m)
function [X,w] = DTFT(x,M)
N = max (M, length(x));
% Приведение FFT к размеру 2^m
N = 2^ (ceil (log (N)/log (2)));
% Вычисление fft
X = fft(x, N);
% Вектор частот
w = 2*pi*( (0:(N-1))/N );
w = w - 2*pi*(w>=pi);
% Сдвиг FFT к интервалу от -pi до +pi
X = fftshift(X);
w = fftshift(w);
Matlab Script (labrab102.m)
N1 = 16;
N2 = 50;
n1 = 0:N1-1;
n2 = 0:N2-1;
wc = 2;
h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
[H1,w] = DTFT(h1,512);
[H2,w] = DTFT(h2,512);
figure (1)
subplot(2,1,1)
plot(w./(2*pi),abs(H1)./max(abs(H1)),'r')
title('АЧХ КИХ-фильтра нижних частот с прямоугольным окном для N = 15')
xlabel('f, Гц'), ylabel('|H1|/max(|H1|)'), grid
subplot(2,1,2)
plot(w./(2*pi),abs(H2)./max(abs(H2)),'b')
title('АЧХ КИХ-фильтра нижних частот с прямоугольным окном для N = 50')
xlabel('f, Гц'), ylabel('|H2|/max(|H2|)'), grid
figure (2)
subplot(2,1,1)
plot(w./(2*pi),20*log10(abs(H1)),'r')
title('АЧХ КИХ-фильтра нижних частот с прямоугольным окном для N = 15')
xlabel('f, Гц'), ylabel('20lg(|H1|), dB'), grid
subplot(2,1,2)
plot(w./(2*pi),20*log10(abs(H2)),'b')
title('АЧХ КИХ-фильтра нижних частот с прямоугольным окном для N = 50')
xlabel('f, Гц'), ylabel('20lg(|H2|), dB'), grid
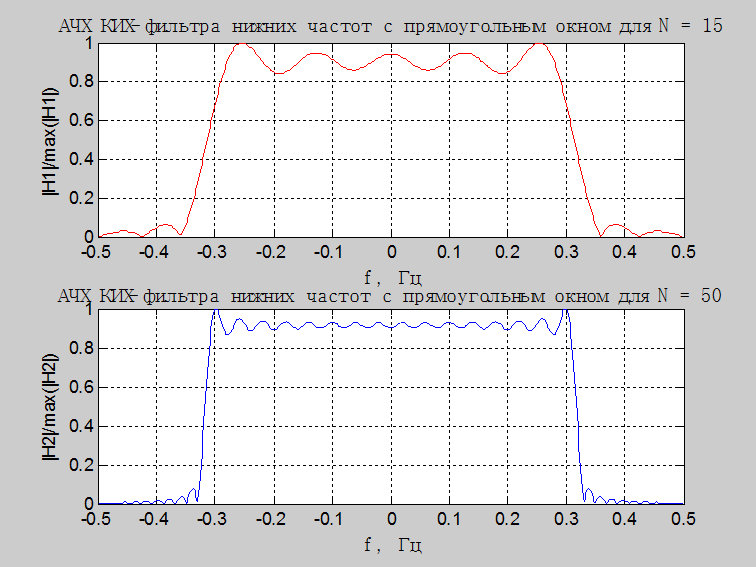
Рис.2. Графики АЧХ КИХ-фильтра
нижних частот с прямоугольным окном частотой среза ![]() для
значений длины фильтра
для
значений длины фильтра ![]() и
и ![]() в линейном масштабе
в линейном масштабе
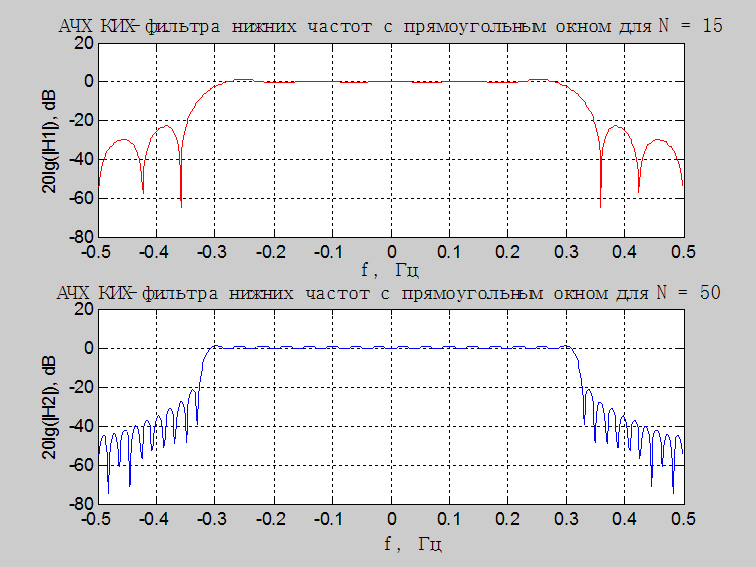
Рис.3. Графики АЧХ КИХ-фильтра
нижних частот с прямоугольным окном частотой среза ![]() для
значений длины фильтра
для
значений длины фильтра ![]() и
и ![]() в логарифмическом масштабе
в логарифмическом масштабе
Комментарий:
Таблица.1. Диапазон
полосы пропускания, переходной области и полосы задерживания для значений
длины фильтра ![]() и
и ![]()
|
Длина фильтра |
Полоса пропускания, Гц |
Переходная область, Гц |
Полоса задерживания, Гц |
|
15 |
0-0,304 |
0,304-0,35 |
от 0,35 |
|
50 |
0-0,314 |
0,314-0,328 |
от 0,328 |
Из приведённой таблицы видно, что
при увеличении порядка фильтра ширина переходной области уменьшается, т.е. спад
становится более крутым (аппроксимация к идеальному фильтру): при ![]() ширина переходной области равна
ширина переходной области равна ![]() , а при
, а при ![]() -
-
![]() , т.е. при увеличении порядка фильтра
в
, т.е. при увеличении порядка фильтра
в ![]() раза – переходная область сузилась
в
раза – переходная область сузилась
в ![]() раза. Это можно наблюдать на рис.2.
раза. Это можно наблюдать на рис.2.
Таблица.2. Уровень
пульсаций в полосе пропускания и полосе задерживания для значений длины
фильтра ![]() и
и ![]()
|
Длина фильтра |
Относительный уровень пульсаций в полосе пропускания, дБ |
Относительный уровень пульсаций в полосе задерживания, дБ |
|
15 |
0,6 |
-23,7 |
|
50 |
0,9 |
-23 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.