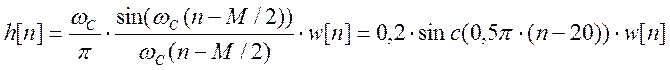Информатика и выч. техника \ Теория и обработка сигналов

Цифровые фильтры с конечной импульсной характеристикой, страница 4

.

Matlab Script (labrab107.m)

M = 41;

n = 0:M-1;

w = 0.5-0.5*cos(2*pi*n/M);

wc = 0.5*pi;

h = w.*(wc*sin(wc.*(n-(M/2))))./(pi*wc*(n-(M/2)));

[H,w] = DTFT(h,512);

plot(w,abs(H))

title('АЧХ спроектированного фильтра')

xlabel('рад/отсчёт')

axis([0,3.14,0,1.2])

grid

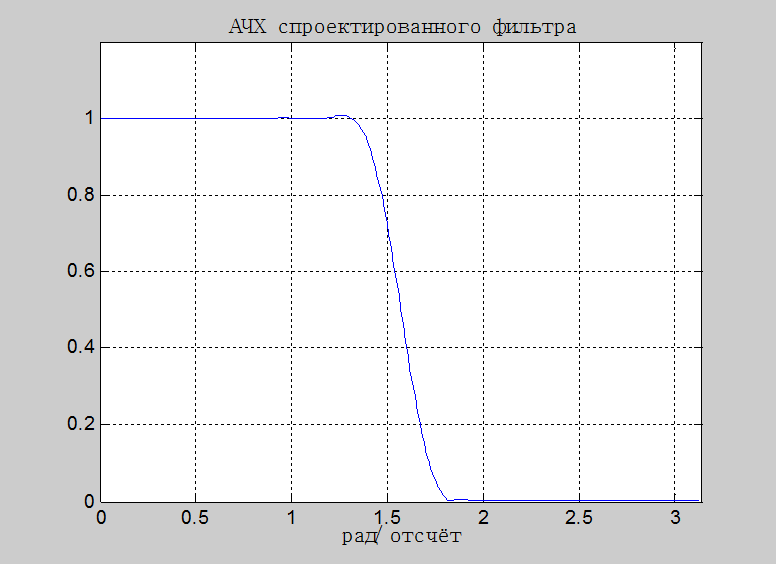
Рис.11. АЧХ спроектированного КИХ-фильтра с окном Ханна

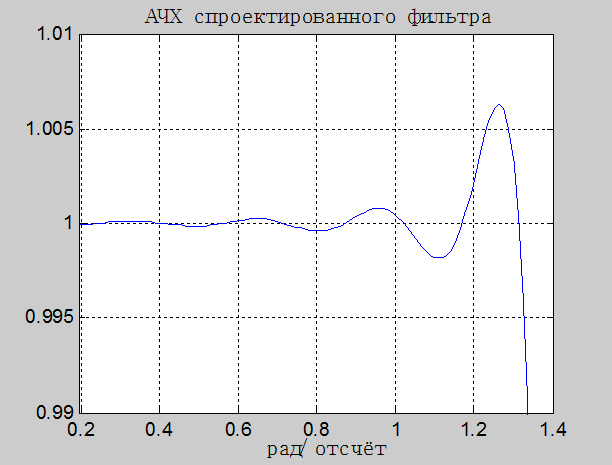
Рис.12. Пульсации в полосе пропускания

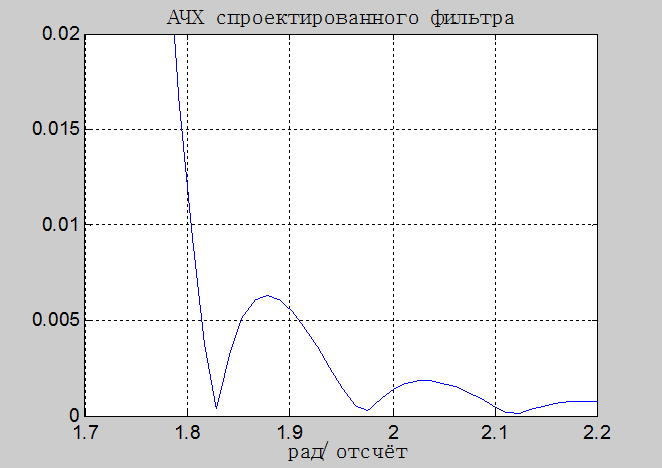
Рис.13. Пульсации в полосе задерживания

Комментарий:

Таблица.7. Проверка соответствия спроектированного фильтра заданным требованиям

Требуемый фильтр

Спроектированный фильтр

1,256

1,314

1,885

1,825

0,02

0,006

0,01

0,006

Исходя из приведённой таблицы, можно сделать вывод о том, что спроектированный фильтр удовлетворяет исходным требованиям.

9.  Фильтрация сигнала  спроектированным фильтром.

>> load('speech.mat');

>> M = 41;

>> n = 0:M-1;

>> w = 0.5-0.5*cos(2*pi*n/M);

>> wc = 0.5*pi;

>> h = w.*(wc*sin(wc.*(n-(M/2))))./(pi*wc*(n-(M/2)));

>> y = conv(nspeech2,h);

>> sound(nspeech2)

>> sound(y)

>> labrab108

Matlab Script (labrab108.m)

[Y,w] = DTFT(nspeech2,512);

subplot(2,1,1)

plot(w./(2*pi),abs(Y))

title ('Амплитудный спектр исходного сигнала')

xlabel('f, Гц')

grid

[Y1,w] = DTFT(y,512);

subplot(2,1,2)

plot(w./(2*pi),abs(Y1))

title ('Амплитудный спектр сигнала после фильтрации спроектированным фильтром')

xlabel('f, Гц')

grid

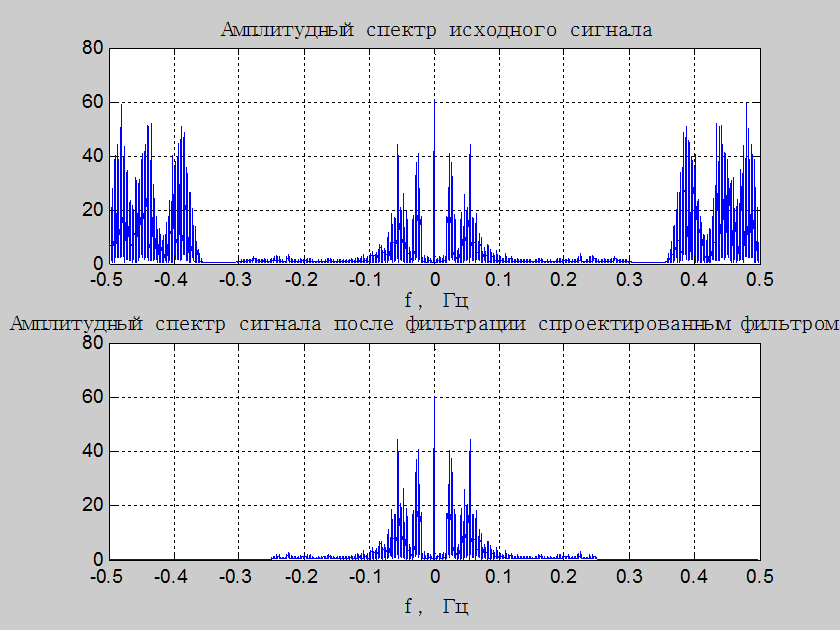
Рис.14. Графики амплитудных спектров исходного сигнала и сигнала после пропускания его через КИХ-фильтр нижних частот с окном Ханна с частотой среза

Комментарий:         Качество звучания исходного сигнала и сигнала, прошедшего через спроектированный фильтр, велико. В исходном сигнале голос зашумлён и имеет слабый, нечёткий звук. В отфильтрованном сигнале шума не слышно и голос звучит достаточно отчётливо. Если сравнивать амплитудный спектр данного выходного сигнала с амплитудными спектрами в п.3, то нетрудно заметить, что в данном случае пульсации в высокочастотной области отсутствуют. Это связано с тем, что, во-первых, граничная частота полосы задерживания у спроектированного фильтра ниже, чем у фильтров из п.3: в данном случае , а у фильтра из п.3  для  - , во-вторых, уровень пульсаций в полосах пропускания и задерживания меньше.  Всё это говорит о том, что спроектированный фильтр достаточно хорош для фильтрации аддитивной смеси  низкочастотного полезного сигнала с высокочастотным шумом.

Вывод по работе:          В данной работе были изучены методы анализа и синтеза КИХ-фильтров с использованием сглаживающих оконных функций. В данной работе были рассмотрены пять видов различных окон:

·  прямоугольное окно,

·  окно Хэмминга,

·  окно Ханна,

·  окно Блэкмана

·  окно Кайзера.

При проектировании КИХ-фильтров разработчик для сглаживания импульсной характеристики в зависимости от заданных требований может выбрать наиболее подходящую оконную функцию. Например, если обратиться к п.8. данной работы, то можно увидеть, что при предъявляемых требованиях (таблица 6) в качестве сглаживающего окна наиболее подходит окно Ханна, так как требуемый допустимый уровень пульсаций равен , а у окна Ханна  - . Далее при проверке соответствия спроектированного фильтра требованиям (таблица 7) стало очевидно, что он полностью отвечает заданным предписаниям.

Вообще, в ходе работы стало ясно, что конкретное окно тем лучше сглаживает, чем уже у него ширина главного лепестка и чем меньше площади под боковыми лепестками. В п.4, п.5 и п.6 были более детально изучены прямоугольное окно, окно Хэмминга, окно Ханна и окно Блэкмана. На рис.5 и рис.6 можно увидеть изображение этих окон. По построенным амплитудным спектрам (рис. 7) этих оконных функций были получены сводные таблицы 3 и 4, которые показывают, что нельзя одновременно получить узкий главный лепесток (и тем самым уменьшить переходную область) и маленький уровень боковых лепестков (и тем самым уменьшить пульсации в полосах пропускания и задерживания). Чем функция  более плавно спадает к нулю, тем меньше уровень пульсаций. Таким образом, из рассматриваемых четырёх оконных функций фильтры, реализованные с прямоугольным окном, будут иметь самую узкую переходную область, а  фильтры, реализованные с окном Блэкмана, - самый маленький уровень пульсаций.

  1. При рассмотрении прямоугольного окна в п.1 было выявлено, что при увеличении длины фильтра, ширина главного лепестка уменьшается: при  ширина главного лепестка составляет 2, а при  - 1, но это не оказывает никакого влияния на боковые лепестки.
  2. Окно Кайзера предоставляет более гибкие возможности по сравнению с другими окнами. Так если в ранее рассмотренных окнах единственным управляемым параметром является длина окна, которая не влияет на уровень пульсаций в полосе пропускания и задерживания, то с помощью же параметра  можно регулировать амплитуду боковых лепестков и форму окна. Из таблицы 5 видно, что при увеличении параметра   ширина главного лепестка окна Кайзера увеличивается, а относительный уровень боковых лепестков уменьшается.

В данной работе так же была произведена фильтрация аддитивной смеси сигнала с шумом с помощью трёх различных КИХ-фильтров: первые два фильтра с прямоугольным окном для  и , а второй с окном Ханна. Самые лучшие результаты фильтрации показал последний фильтр, так как полностью погасил высокочастотный шум, т.о. очистив полезный сигнал. Если сравнивать графики амплитудных спектров для выходных сигналов трёх фильтров (рис.4 и рис.14), то видно, что в последнем случае никаких всплесков в высокочастотной области не наблюдается в отличие от двух других фильтров. Это связано с тем, что, во-первых, граничная частота полосы задерживания у последнего фильтра ниже, чем у фильтров из п.3: в данном случае , а у фильтра из п.3  для  - , во-вторых, уровень пульсаций в полосах пропускания и задерживания меньше.

Скачать файл