Комментарий: Из полученных графиков видно, что у прямоугольного окна самая маленькая ширина главного лепестка, а у окна Блэкмана – самая большая. Уровень боковых лепестков у окна Блэкмана самый низкий, а у прямоугольного окна – самый высокий. Т.е. прямоугольное окно не позволяет получить допустимый уровень пульсаций в полосах пропускания и задерживания, но обеспечивает более крутой спад в переходной области по сравнению с другими оконными функциями, а окно Блэкмана позволяет получить всё в точности наоборот.
6. Определение ширины главного лепестка и относительный уровень боковых лепестков в децибелах (относительно амплитуды главного лепестка).
Таблица.3. Теоретические и соответствующие им измеренные значения ширины главного лепестка, а также разность между этими значениями для четырёх типов окон: прямоугольного, Ханна, Хэмминга и Блэкмана
|
Тип окна |
Ширина главного лепестка (измеренная) |
Ширина главного лепестка (теоретическая) |
Разница, |
|
Прямоугольное окно |
0,54 |
0,524 |
0,016 |
|
Окно Хэмминга |
1,104 |
1,047 |
0,057 |
|
Окно Ханна |
1,055 |
1,047 |
0,008 |
|
Окно Блэкмана |
1,595 |
1,571 |
0,024 |
Таблица.4. Теоретические и соответствующие им измеренные значения относительного уровня боковых лепестков, а также разность между этими значениями для четырёх типов окон: прямоугольного, Ханна, Хэмминга и Блэкмана
|
Тип окна |
Относительный уровень боковых лепестков (измеренный), ДБ |
Относительный уровень боковых лепестков (теоретический), ДБ |
Разница, |
|
Прямоугольное окно |
-13,2 |
-13 |
-0,2 |
|
Окно Хэмминга |
-42,3 |
-41 |
-1,3 |
|
Окно Ханна |
-31,6 |
-31 |
-0,6 |
|
Окно Блэкмана |
-58 |
-57 |
-1 |
Комментарий: Измеренные
значения в целом соответствуют теоретическим, погрешность составляет в среднем
при измерении ширины главного лепестка – около ![]() ,
а при измерении значения относительного уровня боковых лепестков – около
,
а при измерении значения относительного уровня боковых лепестков – около ![]() . Погрешность возникла вследствие
измерений «на глаз» (с помощью
. Погрешность возникла вследствие
измерений «на глаз» (с помощью ![]() ). Из полученных
результатов видно, что у прямоугольного окна ширина главного лепестка меньше
в два раза, чем у окон Хэмминга и Ханна, и в три раза, чем у окна
Блэкмана. А относительный уровень пульсаций по сравнению с окном Блэкмана у
окна Ханна в
). Из полученных
результатов видно, что у прямоугольного окна ширина главного лепестка меньше
в два раза, чем у окон Хэмминга и Ханна, и в три раза, чем у окна
Блэкмана. А относительный уровень пульсаций по сравнению с окном Блэкмана у
окна Ханна в ![]() раза больше, у окна Хэмминга – в
раза больше, у окна Хэмминга – в ![]() , а у прямоугольного окна – в
, а у прямоугольного окна – в ![]() раз.
раз.
7.
Графики окон Кайзера и их амплитудные спектры для ![]() ,
, ![]() ,
, ![]() и
и ![]() .
Влияние значения параметра
.
Влияние значения параметра ![]() на форму окна и
уровень боковых лепестков.
на форму окна и
уровень боковых лепестков.
![]() -
возвращает
-
возвращает ![]() - ценные
- ценные ![]() - значений окна Кайзера.
- значений окна Кайзера.
Окно Кайзера предоставляет более
гибкие возможности по сравнению с другими окнами. Так если в ранее рассмотренных
окнах единственным управляемым параметром является длина окна, которая не
влияет на уровень пульсаций в полосе пропускания и задерживания, то с помощью
же параметра ![]() можно регулировать амплитуду боковых
лепестков и форму окна.
можно регулировать амплитуду боковых
лепестков и форму окна.
а. Окно
Кайзера для ![]() :
:
k1 = kaiser(25,0);
subplot(2,1,1)
stem(k1)
title('Окно Кайзера для N=25 и b=0')
xlabel('Номер отсчёта, n')
[K1,w] = DTFT(k1,512);
subplot(2,1,2)
plot(w,abs(K1))
title('Амплитудный спектр окна Кайзера для N=25 и b=0')
xlabel('рад/отсчёт')
ylabel('|K1|')
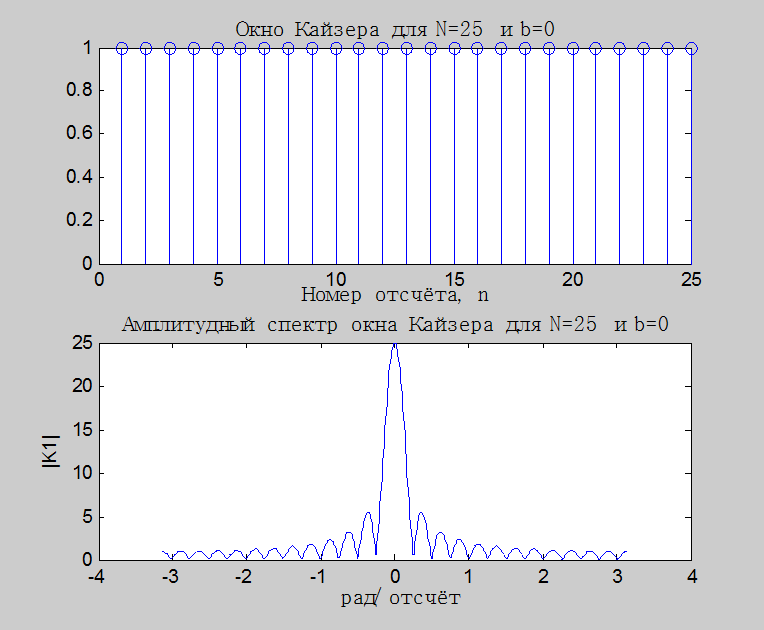
Рис.8. Графики окна
Кайзера и его амплитудного спектра для ![]()
б. Окно
Кайзера для ![]() :
:
k1 = kaiser(25,1);
subplot(2,1,1)
stem(k1)
title('Окно Кайзера для N=25 и b=1')
xlabel('Номер отсчёта, n')
[K1,w] = DTFT(k1,512);
subplot(2,1,2)
plot(w,abs(K1))
title('Амплитудный спектр окна Кайзера для N=25 и b=1')
xlabel('рад/отсчёт')
ylabel('|K1|')
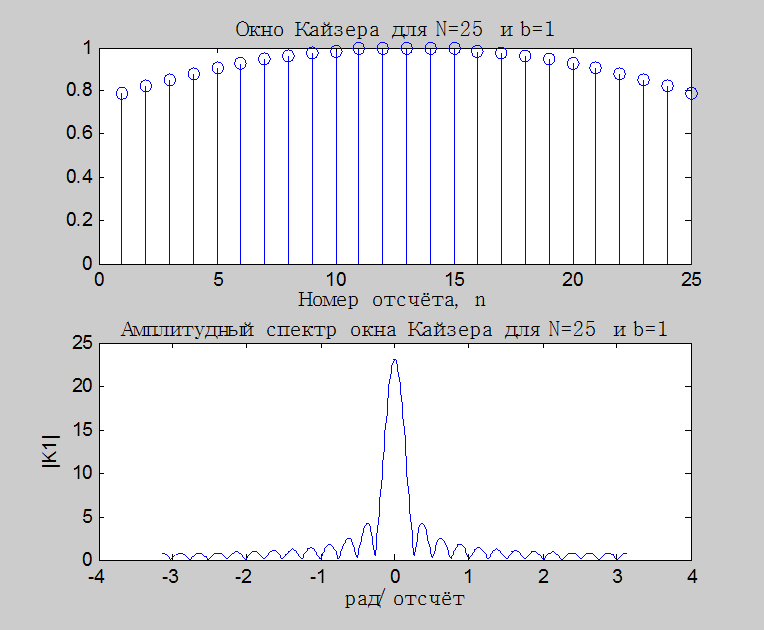
Рис.9. Графики окна
Кайзера и его амплитудного спектра для ![]()
в. Окно
Кайзера для ![]() :
:
k1 = kaiser(25,5);
subplot(2,1,1)
stem(k1)
title('Окно Кайзера для N=25 и b=5')
xlabel('Номер отсчёта, n')
[K1,w] = DTFT(k1,512);
subplot(2,1,2)
plot(w,abs(K1))
title('Амплитудный спектр окна Кайзера для N=25 и b=5')
xlabel('рад/отсчёт')
ylabel('|K1|')
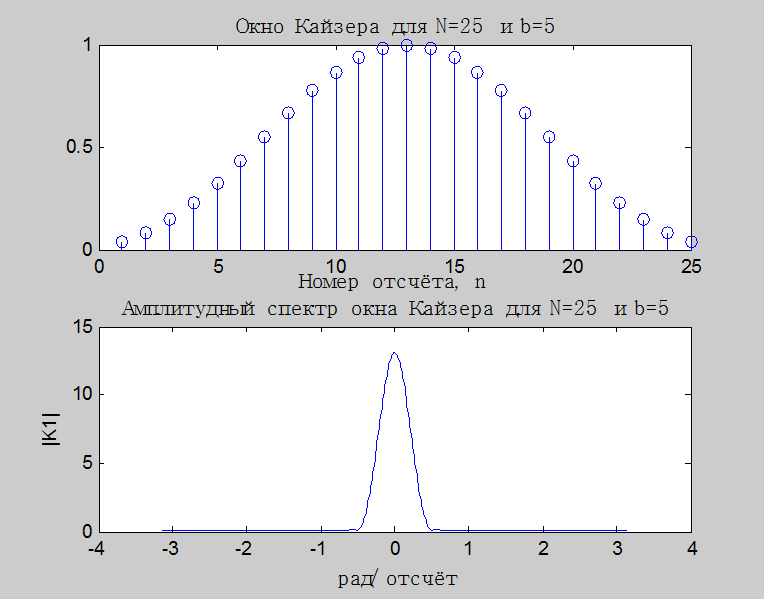
Рис.10. Графики окна
Кайзера и его амплитудного спектра для ![]()
Комментарий:
Таблица.5. Значения
ширины главного лепестка и уровня боковых лепестков в амплитудном спектре окна
Кайзера для различных значений ![]()
|
Значение
коэффициента |
Ширина главного лепестка (измеренная) |
Уровень боковых лепестков |
Относительный уровень боковых лепестков, дБ |
|
0 |
0,5 |
5,45 |
-13,2 |
|
1 |
0,54 |
4,22 |
-14,75 |
|
5 |
1 |
0,16 |
-38 |
При значении параметра ![]() окно Кайзера представляет собой
прямоугольной окно, что можно наблюдать на рис.8, а также сравнив результаты
таблиц 3, 4 и5. При увеличении параметра
окно Кайзера представляет собой
прямоугольной окно, что можно наблюдать на рис.8, а также сравнив результаты
таблиц 3, 4 и5. При увеличении параметра ![]() форма
окна начинает сглаживаться, т.е. происходит более плавное приближение к нулю.
Если при
форма
окна начинает сглаживаться, т.е. происходит более плавное приближение к нулю.
Если при ![]() форма окна мало отличается от
прямоугольного окна (сглаживание происходит лишь на фронтах), то при
форма окна мало отличается от
прямоугольного окна (сглаживание происходит лишь на фронтах), то при ![]() окно Кайзера похоже на окно
Хэмминга, да и сравнив значения соответствующих таблиц можно сделать
аналогичный вывод. Проанализировав данные таблицы 5 можно увидеть, что при
увеличении параметра
окно Кайзера похоже на окно
Хэмминга, да и сравнив значения соответствующих таблиц можно сделать
аналогичный вывод. Проанализировав данные таблицы 5 можно увидеть, что при
увеличении параметра ![]() ширина главного лепестка
окна Кайзера увеличивается, а относительный уровень боковых лепестков уменьшается.
Таким образом, окно Кайзера позволяет не только регулировать ширину переходной
области, но по сравнению с другими оконными функциями, даёт возможность
регулировать амплитуду пульсаций в полосах пропускания и задерживания.
ширина главного лепестка
окна Кайзера увеличивается, а относительный уровень боковых лепестков уменьшается.
Таким образом, окно Кайзера позволяет не только регулировать ширину переходной
области, но по сравнению с другими оконными функциями, даёт возможность
регулировать амплитуду пульсаций в полосах пропускания и задерживания.
8. Синтез фильтра. АЧХ спроектированного фильтра.
Таблица.6. Требования к синтезируемому фильтру
|
|
|
|
|
|
0,4π |
0,6π |
0,02 |
0,01 |
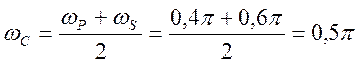 .
.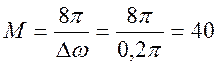 .
.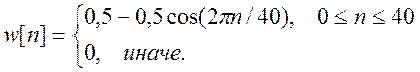
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.