Цифровые фильтры с конечной импульсной характеристикой, страница 2

Из-за усечения импульсной характеристики фильтра (конечное число членов ряда Фурье) можно наблюдать явление Гиббса - появление пульсаций в полосах пропускания и задерживания, возникающих у сигналов с разрывами поведения функций. На рис.3 видно, что пульсации с увеличением порядка фильтра становятся более узкими, и их число увеличивается, но амплитуда пульсаций остаётся практически неизменной. При  число пульсаций в полосе пропускания на рис.2 равно 2, а при  - 8.

3.  Фильтрация сигнала  с использованием операции свёртки.

 - вычисляет свёртку последовательностей  и ,  - сигнал на выходе дискретной системы с импульсной характеристикой  и входным сигналом  при нулевых начальных условиях.

>> load('speech.mat');

>> N1 = 16;

>> N2 = 50;

>> n1 = 0:N1-1;

>> n2 = 0:N2-1;

>> wc = 2;

>> h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));

>> h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));

>> y1 = conv(nspeech2,h1);

>> y2 = conv(nspeech2,h2);

>> sound(nspeech2)

>> sound(y1)

>> sound(y2)

>> labrab103

Matlab Script (labrab103.m)

[Y,w] = DTFT(nspeech2,512);

subplot(3,1,1)

plot(w./(2*pi),abs(Y))

title ('Амплитудный спектр исходного сигнала')

xlabel('f, Гц')

grid

[Y1,w] = DTFT(y1,512);

subplot(3,1,2)

plot(w./(2*pi),abs(Y1))

title ('Амплитудный спектр сигнала после фильтрации (N=15)')

xlabel('f, Гц')

grid

[Y2,w] = DTFT(y2,512);

subplot(3,1,3)

plot(w./(2*pi),abs(Y2))

title ('Амплитудный спектр сигнала после фильтрации (N=50)')

xlabel('f, Гц')

grid

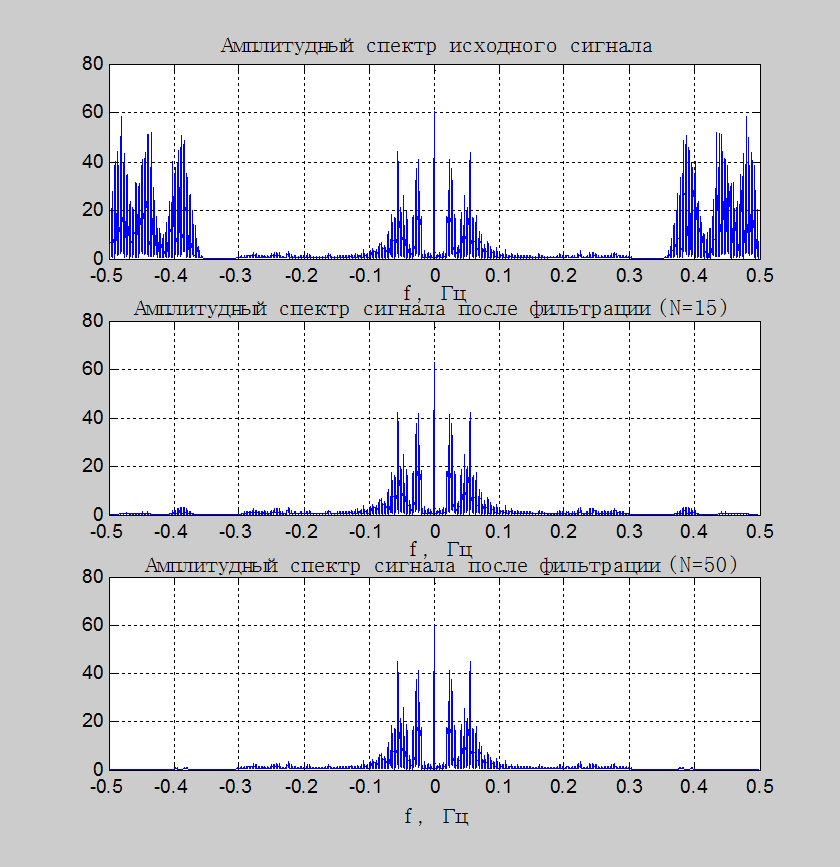
Рис.4. Графики амплитудных спектров исходного сигнала, сигнала после пропускания его через КИХ-фильтр нижних частот с прямоугольным окном частотой среза  для значений  длины фильтра   и  соответственно

Комментарий:         Исходный сигнал представляет собой аддитивную смесь полезного сигнала (речь) с шумом. При его прослушивании на фоне речи слышны «шипящие» звуки. Если обратиться к рис.4, то можно увидеть,  что исходный сигнал состоит из низкочастотной и высокочастотной составляющих. При фильтрации исходного сигнала ФНЧ, длина которого равна , выходной сигнал будет содержать только низкочастотную составляющую, а высокочастотная практически вся подавляется, так как попадает в полосу задерживания фильтра. На рис.4 видно, что в амплитудном спектре выходного сигнала в области высоких частот имеются небольшие всплески, однако же, они по амплитуде раз в  меньше, чем у исходного сигнала. При прослушивании этого сигнала заметно большое подавление помехи, т.е. звук стал чище. При фильтрации исходного сигнала ФНЧ, длина которого равна , в амплитудном спектре выходного сигнала в области высоких частот всплески по сравнению с фильтрацией предыдущим ФНЧ стали ещё меньше – это объясняется тем, что граничная частота полосы задерживания у второго ФНЧ располагается ниже по оси частот. В отфильтрованном сигнале помеха прослушивается плохо, полезный сигнал стал более громким и на  его фоне слышан лишь низкочастотный гул. Таким образом, чем больше порядок КИХ-фильтра нижних частот, тем он больше подходит для выделения полезного низкочастотного сигнала из его смеси с высокочастотным шумом.

4.  Графики прямоугольного окна и окон Хэмминга, Ханна, Блэкмана для .

 - возвращает - значений симметричного окна Хэмминга.

 - возвращает - значений симметричного окна Ханна.

 - возвращает - значений симметричного окна Блэкмана.

Matlab Script (labrab104.m)

N = 25;

n = 0:N-1;

h1 = rectpuls(n-12,N);

h2 = hamming(N);

h3 = hann(N);

h4 = blackman(N);

subplot(4,1,1)

stem(n,h1,'r')

title('Прямугольное окно')

xlabel('Номер отсчёта, n')

axis([-1,25,0,1.5])

subplot(4,1,2)

stem(n,h2,'b')

title('Окно Хэмминга')

xlabel('Номер отсчёта, n')

axis([-1,25,0,1.5])

subplot(4,1,3)

stem(n,h3,'m')

title('Окно Ханна')

xlabel('Номер отсчёта, n')

axis([-1,25,0,1.5])

subplot(4,1,4)

stem(n,h4,'g')

title('Окно Блэкмана')

xlabel('Номер отсчёта, n')

axis([-1,25,0,1.5])

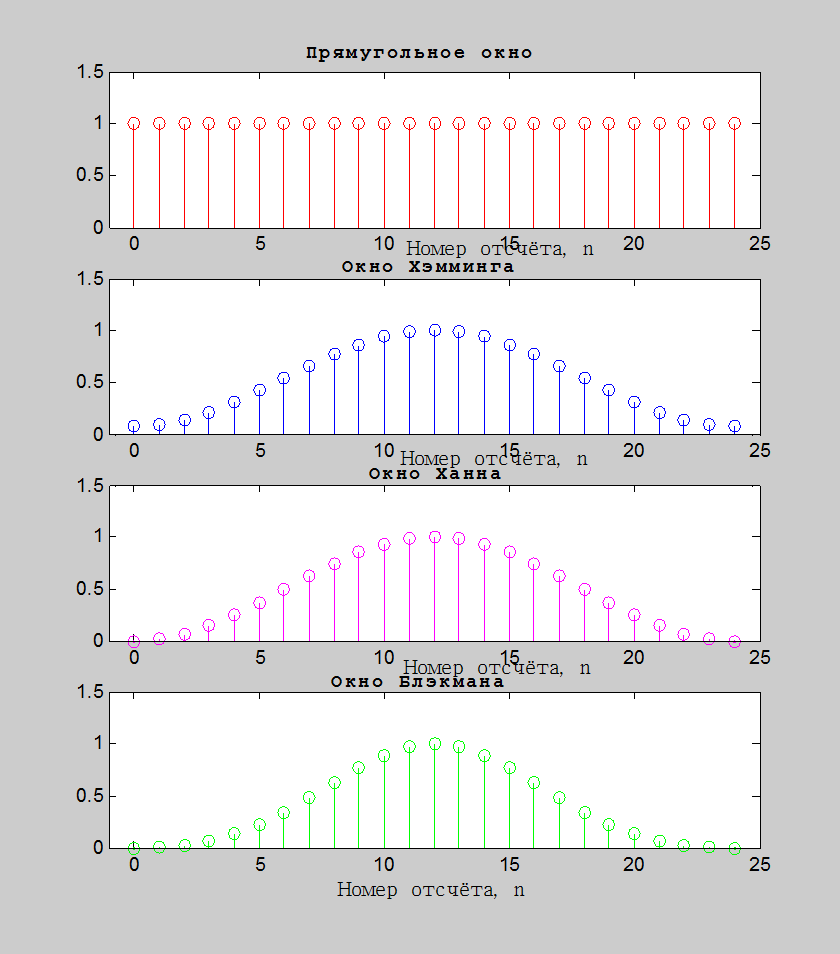
Рис.5. Графики прямоугольного окна, окна Хэмминга, окна Ханна и окна Блэкмана для

Matlab Script (labrab105.m)

N = 25;

n = 0:N-1;

h1 = rectpuls(n-12,N-2);

h2 = hamming(N);

h3 = hann(N);

h4 = blackman(N);

plot(n,h1,'r',n,h2,'b',n,h3,'m',n,h4,'g')

legend('Прямугольное окно','Окно Хэмминга','Окно Ханна','Окно Блэкмана')

axis([-1,25,0,1.5])

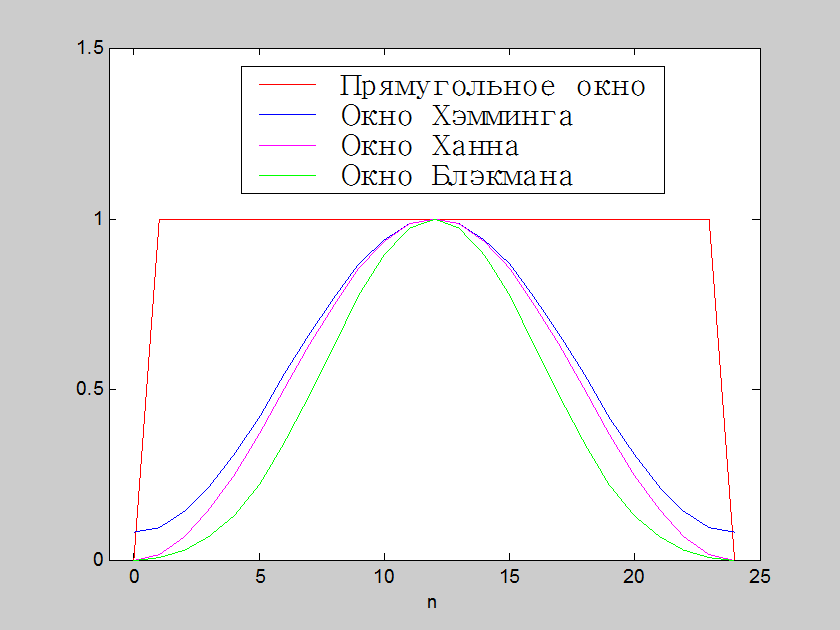
Рис.6. Графики огибающих прямоугольного окна, окна Хэмминга, окна Ханна и окна Блэкмана для

Комментарий:         Сглаживающие окна применяются для улучшения характеристик фильтра. Основными задачами при аппроксимации идеальной АЧХ фильтра  являются – уменьшение переходной области и уменьшение пульсаций в полосах пропускания и задерживания. В зависимости от предъявляемых требований к проектируемому фильтру разработчик выбирает ту или иную оконную функцию для ограничения размера импульсной характеристики. Чем функция  более плавно спадает к нулю, тем меньше уровень пульсаций. Таким образом, из рассматриваемых четырёх оконных функций фильтры, реализованные с прямоугольным окном, будут иметь самую узкую переходную область, а  фильтры, реализованные с окном Блэкмана, - самый маленький уровень пульсаций.

5.  Вычисление ДВПФ оконных функций из предыдущего пункта. Графики амплитудных спектров.

Matlab Script (labrab106.m)

N = 25;

n = 0:N-1;

h1 = rectpuls(n-12,N-2);

h2 = hamming(N);

h3 = hann(N);

h4 = blackman(N);

[H1,w]=DTFT(h1,512);

[H2,w]=DTFT(h2,512);

[H3,w]=DTFT(h3,512);

[H4,w]=DTFT(h4,512);

subplot(4,1,1), plot(w,20*log10(abs(H1)))

title('Амплитудный спектр прямугольного окна'), ylabel('dB')

grid, axis([0,3.2,-50,50])

subplot(4,1,2), plot(w,20*log10(abs(H2)))

title('Амплитудный спектр окна Хэмминга'), ylabel('dB')

grid, axis([0,3.2,-100,50])

subplot(4,1,3), plot(w,20*log10(abs(H3)))

title('Амплитудный спектр окна Ханна'), ylabel('dB')

grid, axis([0,3.2,-100,50])

subplot(4,1,4), plot(w,20*log10(abs(H4)))

title('Амплитудный спектр окна Блэкмана'), xlabel('рад/отсчёт'), ylabel('dB')

grid, axis([0,3.2,-150,50])

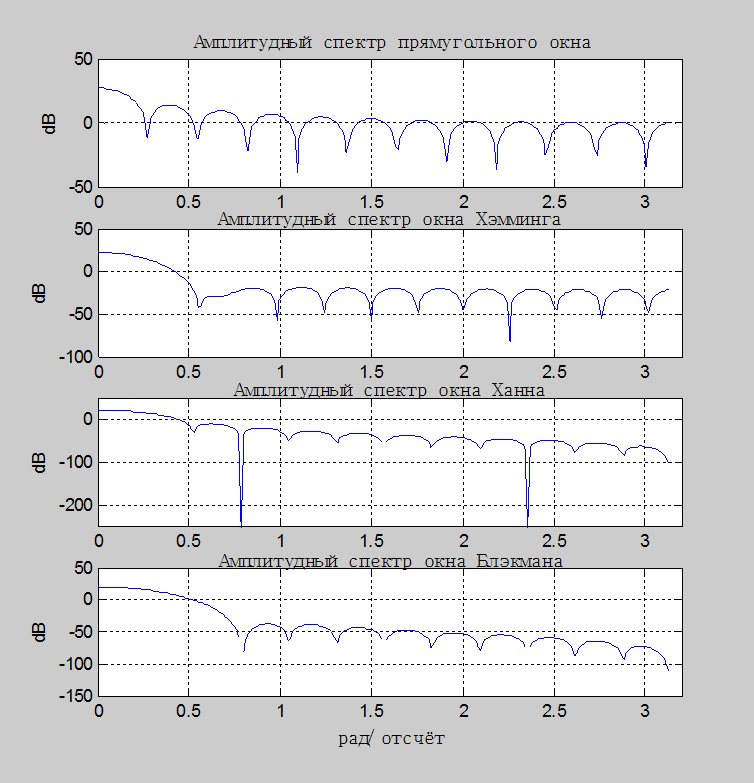
Рис.7. Графики амплитудных спектров прямоугольного окна, окна Хэмминга, окна Ханна и окна Блэкмана для