Математика \ Вычислительная математика

Среднеквадратичная аппроксимация функций. Вариант 6

Страницы работы

16 страниц (Word-файл)

Скачать файл

Содержание работы

Министерство образования Российской Федерации

Новосибирский Государственный Технический Университет

Вычислительная математика

РАСЧЕТНО - ГРАФИЧЕСКАЯ РАБОТА

на тему

«СРЕДНЕКВАДРАТИЧНАЯ АППРОКСИМАЦИЯ ФУНКЦИЙ»

Выполнила: Проверил:

студентка 2 курса АВТФ Соловьёв А. Л.

группы АА-16

вариант 6

Мокроусова В. В.

Новосибирск

2003 г.

1.Постановка задачи

На интервале произвести аппроксимацию реализации функции , заданной на с шагом (в таблице функция приведена в аналитическом виде), обобщенным рядом Фурье по системе ортогональных (ортонормированных) на с весом базисных функций .

Определить на погрешности аппроксимации.

Проанализировать влияние числа учитываемых членов ряда Фурье на точность аппроксимации изменяя параметр от до с шагом .

Варианты задания приведены в табл.1

Табл.1

№ п/п	Вид аппроксимируемой функции	Интервал	Шаг	Базисные функции
6		[0,75; 2,35]	0,025	Чебышева

2. Основные теоретические положения

Произвольную, кусочно-непрерывную функцию на интервале приближенно можно представить в виде обобщенного ряда Фурье с конечным числом членов

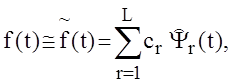(1.1)

где , - система ортогональных с весом на базисных функций, а

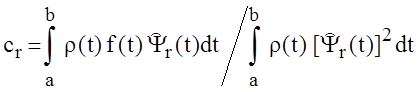(1.2)

коэффициенты Фурье.

Таким образом, чтобы решить задачу аппроксимации функции на , необходимо при заданном базисе , вычислить коэффициенты Фурье согласно (1.2) и восстановить оценку аппроксимируемой функции по выражению (1.1).

Ниже приведены ортогональные (ортонормированные) с весом на базисные функции, используемые при решении задачи аппроксимации.

Полиномы Лежандра, ортогональные на с весом , удобно вычислять на ЭВМ по рекуррентной формуле:

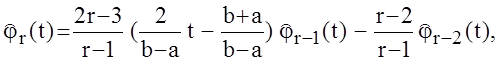(1.3)

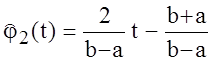Нормирующий множитель полиномов Лежандра имеет вид:

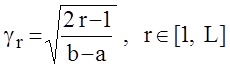(1.4)

и ортонормированные полиномы Лежандра могут вычисляться как

(1.5)

Полиномы Чебышева первого рода, ортогональные на с весом

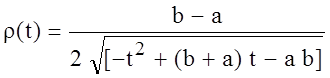(1.6)

также могут вычисляться по рекуррентной формуле:

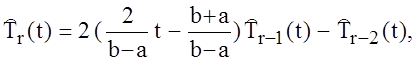(1.7)

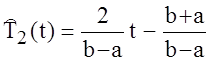Нормирующий множитель полиномов Чебышева первого рода

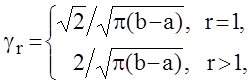(1.8)

а ортонормированные полиномы Чебышева первого рода определяются в виде

. (1.9)

При вычислении на ЭВМ коэффициентов ряда Фурье по полиномам Чебышева в моменты времени t = a и t = b подкоренное выражение в весовой функции обращается в нуль. Чтобы избежать операции деления на нуль, в подкоренное выражение можно ввести некоторый малый параметр (например , где - шаг дискретизации). Однако введение параметра приводит к дополнительной погрешности в вычислениях коэффициентов Фурье, что в конечном итоге сказывается на погрешности аппроксимации. Причем, как показывает практика, погрешности, порожденные параметром , оказываются соизмеримыми с погрешностями от отбрасывания остаточного члена ряда Фурье при L = 3, 4 при аппроксимации на полупериода синусоиды.

Тригонометрические функции, ортонормированные на с весом =1

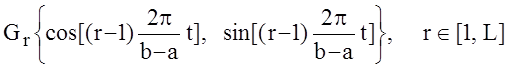(1.10)

образуют гармонический ряд Фурье, который представляется в виде

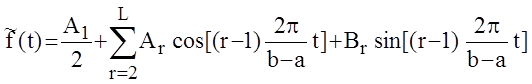, (1.11)

где

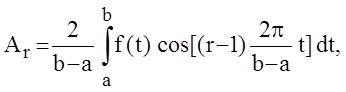
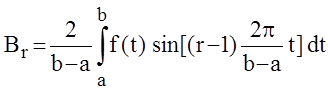. (1.12)

Функции Лагерра, ортонормированные на с весом =1, могут быть вычислены по рекуррентной формуле

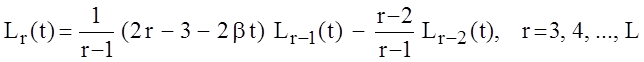, (1.13)

Параметр , фигурирующий в выражениях функций Лагерра, необходимо выбирать из условия сохранения их свойств при аппроксимации не на бесконечном, а на конечном интервале времени, что имеет место при практическом использовании этих функций. Речь идет о количестве нулей функций Лагерра на заданном интервале аппроксимации, а именно, если имеет нулей на , то и на она должна иметь нулей.

Экспериментально было установлено, что параметр следует выбирать в виде

(1.14)

При этом амплитуда L-й функции Лагерра в точке T будет составлять не более 0,1 от максимального на значения этой функции.

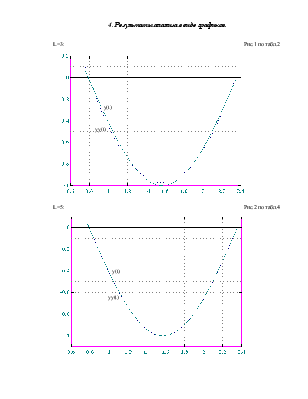
При анализе погрешностей аппроксимации следует иметь в виду, что при выполнении данной работы на ЭВМ результирующая погрешность включает в себя две составляющие: методическую, возникающую из-за отбрасывания остаточного члена

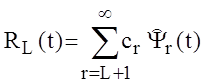
и вычислительную (погрешность округления на ЭВМ). Исходные данные полагаем заданными точно, поэтому погрешность задания исходных данных отсутствует.

Точность аппроксимации на обобщенным рядом Фурье следует оценивать посредством следующих погрешностей:

- максимальной на абсолютной и относительной

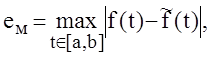
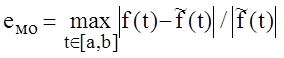; (1.15)

- среднеквадратичной на абсолютной и относительной

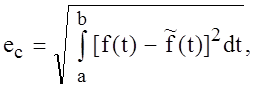
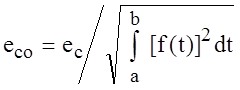. (1.16)

3. Листинг программы:

program kursovaia rabota

integer n,l

DIMENSION y(300),ro(300),y1(300),c(10)

dimension al3(3,300),al4(4,300),al5(5,300),al6(6,300)

DIMENSION yy(300),e(300),al7(7,300)

real a,b,dt,x,em,es,ep,emo,eso,epo

open (1,file='kto.txt')

write (1,*)'Студентка: Мокроусова Вера Валерьевна'

write (1,*)'Группа: АА-16'

write (1,*)'Вариант N6'

write (1,*)'Исходные данные: a=0.75;b=2.35;dt=0,025;'

write (1,*)'Аппроксимируемая функция: COS(2*t);'

write (1,*)'Базисные функции Чебышева.'

a=0.75

b=2.35

dt=0.025

n=(b-a)/dt+1

do 1 i=1,n

x=a+dt*(i-1)

y(i)=cos(2*x)

1 continue

OPEN(8,FILE='1.txt')

OPEN(9,FILE='c.txt')

write(8,*)' L Emo Eco'

do 3 l=3,7

if(l.EQ.3)goto 33

if(l.EQ.4)goto 34

if(l.EQ.5)goto 35

if(l.EQ.6)goto 36

if(l.EQ.7)goto 37

33 OPEN(7,FILE='3.txt')

CALL N1Ypth(a,b,n,dt,l,ro,al3)

CALL N1YKF(n,dt,l,y,y1,al3,ro,c)

CALL N1YWst(n,l,c,al3,yy)