Требования и примерные варианты расчётно-графических заданий по курсу «Вычислительная математика»

2.9. Расчётно-графическое задание. Требования и примерные варианты.

            Содержание расчётно-графического задания выдаётся преподавателем индивидуально каждому студенту академической группы и может варьироваться для различных групп студентов. Задание содержит шесть задач различного уровня сложности.

            При выполнении задания следует руководствоваться правилами и рекомендациями, как и в случае выполнения типового расчёта по математике, а именно:

•  научиться применять основные положения теории при решении стандартных, типовых задач;
• приобрести навык решения нестандартных задач при выполнении теоретических упражнений;
• аккуратно и правильно оформлять результаты работы;
• закрепить основные положения темы в целом при подготовке к защите задания.

Расчётно-графическое задание по курсу «Вычислительная математика» введено для лучшего усвоения курса и повышения результативности самостоятельной работы.

Время выдачи и защиты задания указано в графике самостоятельной работы.

При выполнении расчётно-графического задания следует приводить предварительно аналитические выражения и формулы с необходимыми пояснениями относительно точности сходимости вычислительных процессов, реализующих данные формулы. На заключительном (расчётном этапе) пользование программно-инструментальными средствами представляется разумным.

Ниже приводится возможный вариант расчётно-графического задания и рассматривается решение одной из задач.

Таблица 2.12

№ задачи	Содержание задачи	Вид аналитического выражения	Точность приближения	Доп. требования
1	Разложить по формуле Тейлора заданную функцию: а) Выбрать точку разложения; б) определить радиус сходимости; в) определить число членов ряда, необходимое для вычисления f(x) с заданной точностью; г) произвести экономизацию степенного ряда, вычисляющего f(x) с точностью ε2.			Полином Чебышева третьего порядка
2	Вычисление комплексных корней			Найти границы существования корней
			Продолжение табл. 2.12
№ задачи	Содержание задачи	Вид аналитического выражения	Точность приближения	Доп. требования
3	Нахождение корней методом обратного интегрирования			Отделить корни графически
4	Разложение функции в цепные дроби
5	Приближение кривых методом наименьших квадратов
6	Методы прогноза и коррекции.			Метод Милна y(0)=1 y|(0)=0

Решение одной из задач.

            В качестве примера возьмём задачу разложения функции в ряд Тейлора (задача №1).

            Поскольку ЭВМ способна непосредственно вычислять только функции, содержащие арифметические операции (полиномы, дробно-рациональные функции, полиномиальные сплайны и т.д.), то большое количество элементарных функций реализуется на вычислительной машине путём замены исходной функции её приближённым аналогом. Обычно используются полиномиальные функции: . Если полная погрешность вычисления на заданном интервале не превышает заданную величину, то приближение исходной функции считается удовлетворительным.

            В нашем примере с помощью арифметических операций невозможно вычислить только функцию sin(x). Разложим sin(x) в ряд Тейлора. Из курса математического анализа известно, что в окрестностях точки разложения x₀=0 функция sin(x) раскладывается в ряд Тейлора следующим образом:

            ,

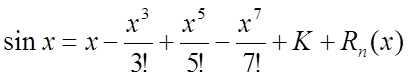где R_n(x) – остаточный член формулы Тейлора.

            Замечание. При разложении более сложных функций в ряд Тейлора необходимо воспользоваться стандартной методикой. При этом точку разложения выбирать из соображений простоты вычисления коэффициентов формулы Тейлора и принадлежности точки разложения интервалу вычисления функции. Радиус сходимости разложения можно определить с помощью признака Даламбера, в отдельных случаях помогают признаки сходимости Коши и Лейбница.

            В нашем примере остаточный член может быть оценён по формуле:

           

            Определимся с интервалом разложения функции. Исходная функция является нечётной функцией, поскольку f(x) = -f(-x), кроме того, она терпит разрывы второго рода в точках, где sin(x) = 0. На рис. 2.11 представлен график функции:

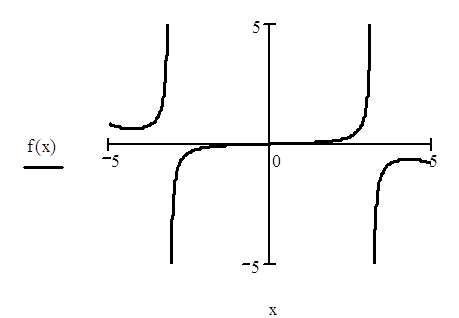
                                    Рис. 2.11

            В точке x = 0 функция терпит устранимый разрыв первого рода, поскольку .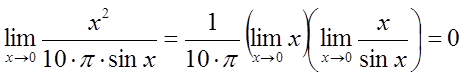

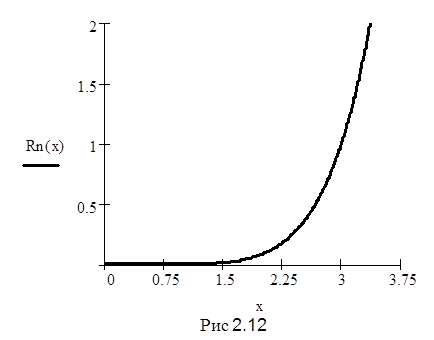
            Будем считать, что вычисления производятся на центральном участке непрерывности функции (-π, π). Учитывая центральную симметрию функции, рассмотрим интервал (0, π). Рассмотрим, каким образом изменяется оценка остаточного члена формулы Тейлора при n = 5 (см. рис. 2.12).

Из графика видно, что при удалении x от точки разложения величина остаточного члена резко увеличивается. Установим связь между полной ошибкой приближённого представления вычисляемой функции и остаточным членом разложения sin(x) по формуле Тейлора. При замене sin(x) имеем:

.

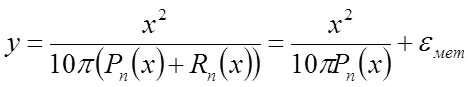            Методическая ошибка в связи с заменой синуса полиномиальной функцией содержится в знаменателе вычисляемой функции, следовательно, по формуле оценки ошибки от деления получим:

            ,

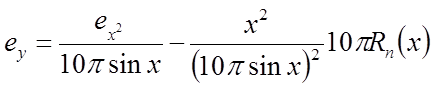учитывая, что 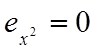 имеем:

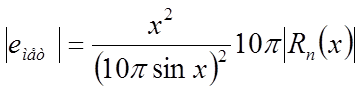
            Если не учитывать погрешности округления, то для оценки числа членов ряда разложения функции sin(x), обеспечивающие заданную точность вычисления функции, можно воспользоваться неравенством:

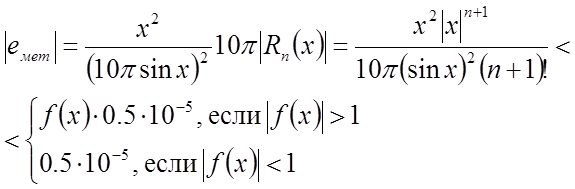                                   (2.65)

            В последней формуле учитывается, что в условии задачи задана величина относительной погрешности вычисления функции.

            Экономизация ряда заключается в уменьшении числа арифметических операций при условии сохранения заданной точности вычисления функции. Данный приём использует свойство полиномов Чебышева сводить к минимуму максимальную ошибку приближения. Экономизация основывается на изменении структуры ряда в сторону увеличения сходимости, при этом в отдельных случаях удаётся уменьшить число членов ряда.

            В нашем примере наибольшая погрешность возникает на правой границе интервала приближения функции, с другой стороны полинома Чебышева действуют на интервале (-1, 1), поэтому вычисления будем производить для x = 0,99.

            Экономизация.

            Экономизация ряда заключается в уменьшении числа арифметических операций при условии сохранения заданной точности вычисления функции. Данный приём использует свойство полиномов Чебышева сводить к минимуму максимальную ошибку приближения. Экономизация основывается на изменении структуры ряда в сторону увеличения сходимости, при этом в отдельных случаях удаётся уменьшить число членов ряда.

            В нашем случае наибольшая погрешность возникает на правой границе интервала приближения функции, с другой стороны полиномы Чебышева действуют на интервале (-1, 1), поэтому вычисления будем производить для x=0,99.

            Замечание. Если вычисление необходимо произвести на более широком интервале (a, b), то предварительно следует провести линейное преобразование системы координат, т.е. ввести новую переменную 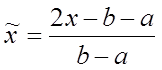, которая принадлежит интервалу (-1, 1), а все вычисления производить для функции .

            Из формулы (2.65) и условий задачи оценим методическую погрешность, с которой необходимо вычислять функцию sin(x).

           

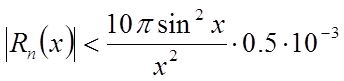
            При x = 0,99 имеем .

            Метод экономизации основывается на замене степенных функций xⁿ разложениями по полиномам Чебышева, например, 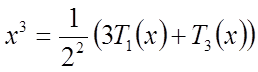. Можно показать, что при таких заменах коэффициент при старшей степенной функции будет равен 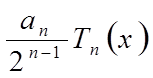, где a_n - коэффициент при старшей степенной функции в формуле Тейлора. Если для знакопеременного

степенного ряда 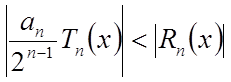, член  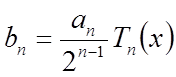можно отбросить.

n	bn	Rn(x)
2	0,25	0,1617165
3	0,0416667	0,0400248
4	0,0052083	0,0079249
5	0,0005208	0,0013076
6	4,34E-05	0,0001849
7	3,1E-06	2,289E-05
8	1,938E-07	2,517E-06
9	1,076E-08	2,492E-07

Таблица 2.13
            В табл. 2.13 верхние оценки остаточного члена в формуле Тейлора при x = 0,99 и коэффициентов при старших членах экономизированного ряда. Из таблицы видно, что для функции sin(x) экономизация возможна начиная с n = 5 на один член рада. В нашем случае при 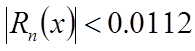 экономизация невозможна.

            Тем не менее, покажем технику экономизации в тех случаях, если это возможно. Пусть n = 5. В этом случае при x = 0,99 .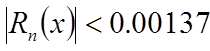

Для 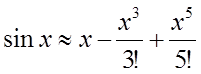, произведя замену 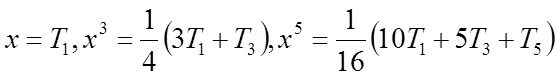, после приведения подобных членов получим: . Отбросив последний член ряда, имеем: .

            Степень последнего многочлена на два порядка меньше, чем в формуле Тейлора, и в то же время удовлетворяет заданной точности вычисления.