write(7,*) ' t y yy eps'
do 2 i=1,n
x=a+(i-1)*dt
write(7,10)x,y(i),yy(i),e(i)
2 continue
CLOSE(7)
3 continue
close(9)
CLOSE(8)
OPEN(9,FILE='p.txt')
write(9,*)'Весовая функция'
OPEN(8,FILE='2.txt')
write(8,*)'Базисные функции'
do 4 i=1,n
x=a+(i-1)*dt
write(9,13)x,ro(i)
write(8,13)x,(al5(j,i),j=1,5)
4 continue
close(9)
close(8)
10 FORMAT(F7.3,F10.6,F10.6,F12.8)
11 FORMAT(I3,F10.6,F10.6)
12 FORMAT(F12.8,F12.8,F12.8,F12.8,F12.8,F12.8,F12.8)
13 FORMAT(F7.3,F12.8,F12.8,F12.8,F12.8,F12.8,F12.8,F12.8)
end
4. Результаты анализа в виде графиков.
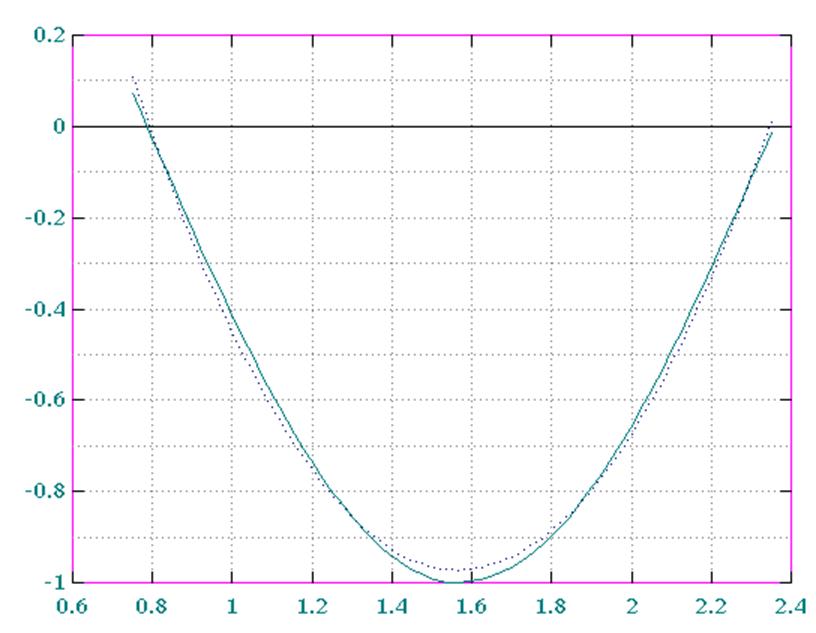
L=3: Рис.1 по табл.2
|
|
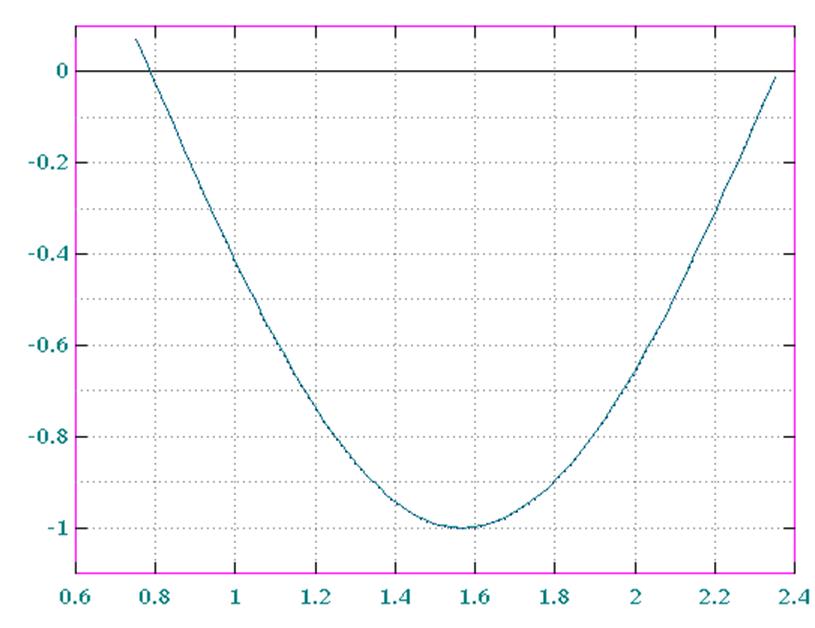
L=5: Рис.2 по табл.4
|
|
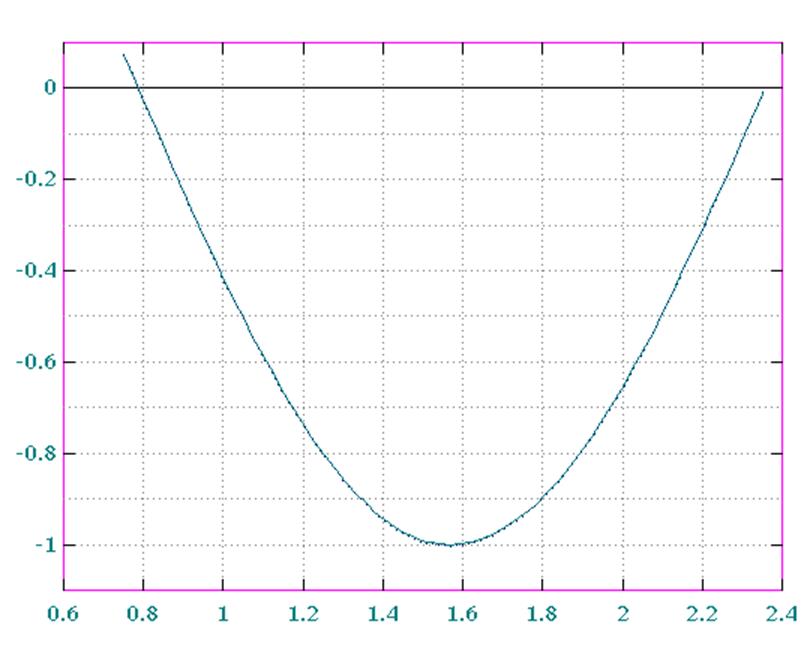
L=7: Рис.3 по табл.6
|
|
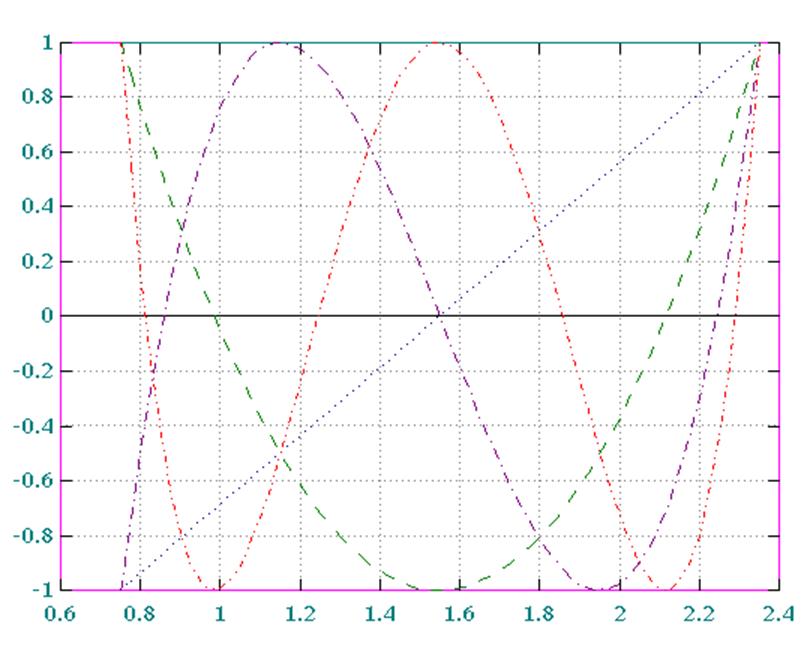
![]() Рис.4 по табл.7
Рис.4 по табл.7
|
|
|
|
|
Погрешности: Рис.5 по табл.9
|
|
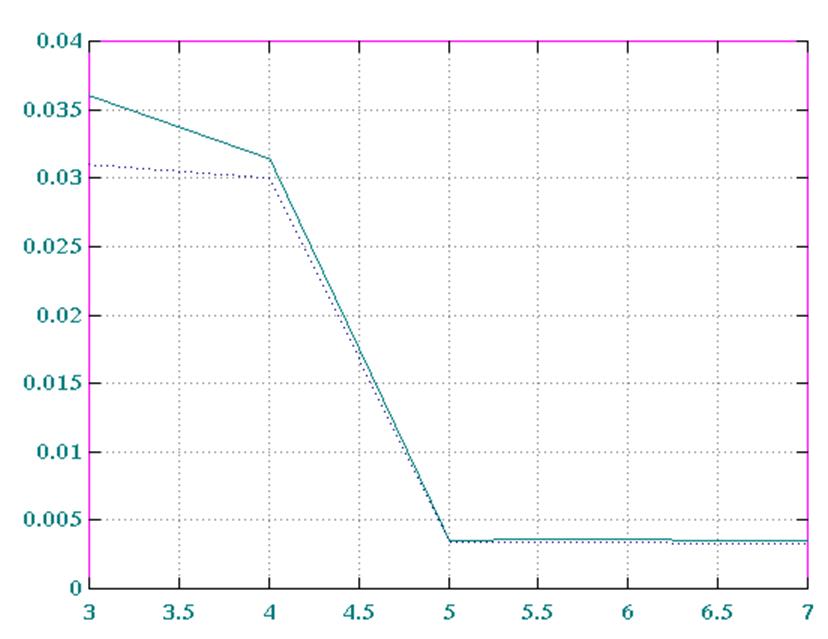
Рис 6 по табл.10
|
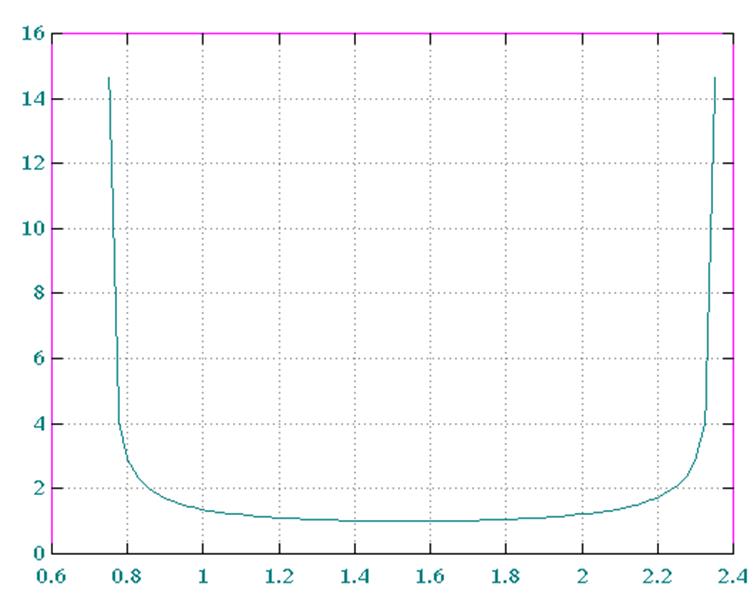
5.Выводы по результатам работы:
Методическая погрешность аппроксимации уменьшается с увеличением числа (L) учитываемых членов ряда Фурье (уменьшаются максимальная относительная погрешность (EMO) и среднеквадратическая относительная погрешность (ESO)); вычислительная же погрешность с ростом L увеличивается. Абсолютная погрешность ввиду этих факторов сначала уменьшается, затем, начиная с некоторого L, растет. То есть существует оптимальное число учитываемых членов ряда Фурье.
6. Приложение (файлы результатов).
L=3:Табл.2
t y yy eps
0.750 0.070737 0.106802 -0.03606458
0.775 0.020795 0.041872 -0.02107725
0.800 -0.029200 -0.021043 -0.00815616
0.825 -0.079121 -0.081945 0.00282368
0.850 -0.128844 -0.140832 0.01198709
0.875 -0.178246 -0.197704 0.01945829
0.900 -0.227202 -0.252563 0.02536081
0.925 -0.275590 -0.305407 0.02981699
0.950 -0.323290 -0.356237 0.03294775
0.975 -0.370181 -0.405053 0.03487232
1.000 -0.416147 -0.451855 0.03570795
1.025 -0.461073 -0.496642 0.03556952
1.050 -0.504846 -0.539415 0.03456926
1.075 -0.547358 -0.580174 0.03281671
1.100 -0.588501 -0.618919 0.03041792
1.125 -0.628174 -0.655650 0.02747595
1.150 -0.666276 -0.690366 0.02408981
1.175 -0.702713 -0.723068 0.02035487
1.200 -0.737394 -0.753756 0.01636195
1.225 -0.770231 -0.782429 0.01219803
1.250 -0.801144 -0.809089 0.00794500
1.275 -0.830054 -0.833734 0.00368023
1.300 -0.856889 -0.856365 -0.00052404
1.325 -0.881582 -0.876981 -0.00460082
1.350 -0.904072 -0.895584 -0.00848836
1.375 -0.924302 -0.912172 -0.01213038
1.400 -0.942222 -0.926746 -0.01547635
1.425 -0.957787 -0.939306 -0.01848143
1.450 -0.970958 -0.949851 -0.02110684
1.475 -0.981702 -0.958383 -0.02331960
1.500 -0.989992 -0.964900 -0.02509278
1.525 -0.995808 -0.969403 -0.02640575
1.550 -0.999135 -0.971891 -0.02724397
1.575 -0.999965 -0.972366 -0.02759904
1.600 -0.998295 -0.970826 -0.02746898
1.625 -0.994130 -0.967272 -0.02685797
1.650 -0.987480 -0.961703 -0.02577633
1.675 -0.978362 -0.954121 -0.02424079
1.700 -0.966798 -0.944524 -0.02227402
1.725 -0.952818 -0.932913 -0.01990503
1.750 -0.936457 -0.919288 -0.01716870
1.775 -0.917754 -0.903649 -0.01410592
1.800 -0.896758 -0.885995 -0.01076347
1.825 -0.873521 -0.866327 -0.00719386
1.850 -0.848100 -0.844645 -0.00345504
1.875 -0.820559 -0.820949 0.00038928
1.900 -0.790968 -0.795238 0.00427032
1.925 -0.759399 -0.767513 0.00811416
1.950 -0.725932 -0.737774 0.01184189
1.975 -0.690651 -0.706021 0.01536995
2.000 -0.653644 -0.672253 0.01860988
2.025 -0.615002 -0.636472 0.02146947
2.050 -0.574824 -0.598676 0.02385199
2.075 -0.533209 -0.558866 0.02565700
2.100 -0.490261 -0.517041 0.02678055
2.125 -0.446087 -0.473203 0.02711529
2.150 -0.400799 -0.427350 0.02655077
2.175 -0.354509 -0.379483 0.02497381
2.200 -0.307333 -0.329602 0.02226868
2.225 -0.259388 -0.277706 0.01831755
2.250 -0.210796 -0.223796 0.01300047
2.275 -0.161676 -0.167872 0.00619613
2.300 -0.112152 -0.109934 -0.00221840
2.325 -0.062348 -0.049982 -0.01236682
2.350 -0.012389 0.011985 -0.02437363
L=4: Табл.3
t y yy eps
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.