МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ
НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
«Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 3
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
НЕПРЕРЫВНЫХ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
Вариант 8
Факультет: АВТ Преподаватель:
Группа: АО-21 Щетинин Ю. И.
Студент: Минин Ю. В.
Новосибирск
2004
Цель работы:Изучение преобразования Фурье и его свойств, понятий амплитудного и фазового спектров непрерывных во времени сигналов, приобретение практических навыков вычисления преобразования Фурье и построения графиков спектров в среде Matlab.
Задание №1:Используем функцию pulstran(…) Matlab для формирования четырех четных последовательностей прямоугольных периодических импульсов.
Файл-сценарий для построения графиков четных последовательностей прямоугольных периодических импульсов:
figure(2)
T1 = -32:1/50:32; % интервал 64с дискретизирован с частотой 50 Гц
D1 = -32:4:32 % вектор задержек – период импульсов 4с, амплитуда=1.
y1 = pulstran(T1,D1,'rectpuls',2);
T2 = -32:1/50:32; % интервал 64с дискретизирован с частотой 50 Гц
D2 = -32:8:32; % вектор задержек - период импульсов 8с, амплитуда=1.
y2 = pulstran(T2,D2,'rectpuls',2);
T3 = -32:1/50:32; % интервал 64с дискретизирован с частотой 50 Гц
D3 = -32:16:32; % вектор задержек - период импульсов 16с
y3 = pulstran(T3,D3,'rectpuls',2);
T4 = -32:1/50:32; % интервал 64с дискретизирован с частотой 50 Гц
D4 = -32:32:32; % вектор задержек - период импульсов 32с
y4 = pulstran(T4,D4,'rectpuls',2);
%построение графиков
subplot(4,1,1),plot(T1,y1),axis([-32,32,0,1.5])
title('T=4 c tau=2 c '),grid on
subplot(4,1,2),plot(T2,y2),axis([-32,32,0,1.5])
title('T=8 c tau=2 c '),grid on
subplot(4,1,3),plot(T3,y3),axis([-32,32,0,1.5])
title('T=16c tau=2 c '),grid on
subplot(4,1,4),plot(T4,y4),axis([-32,32,0,1.5])
title('T=32 c tau=2 c '),grid on
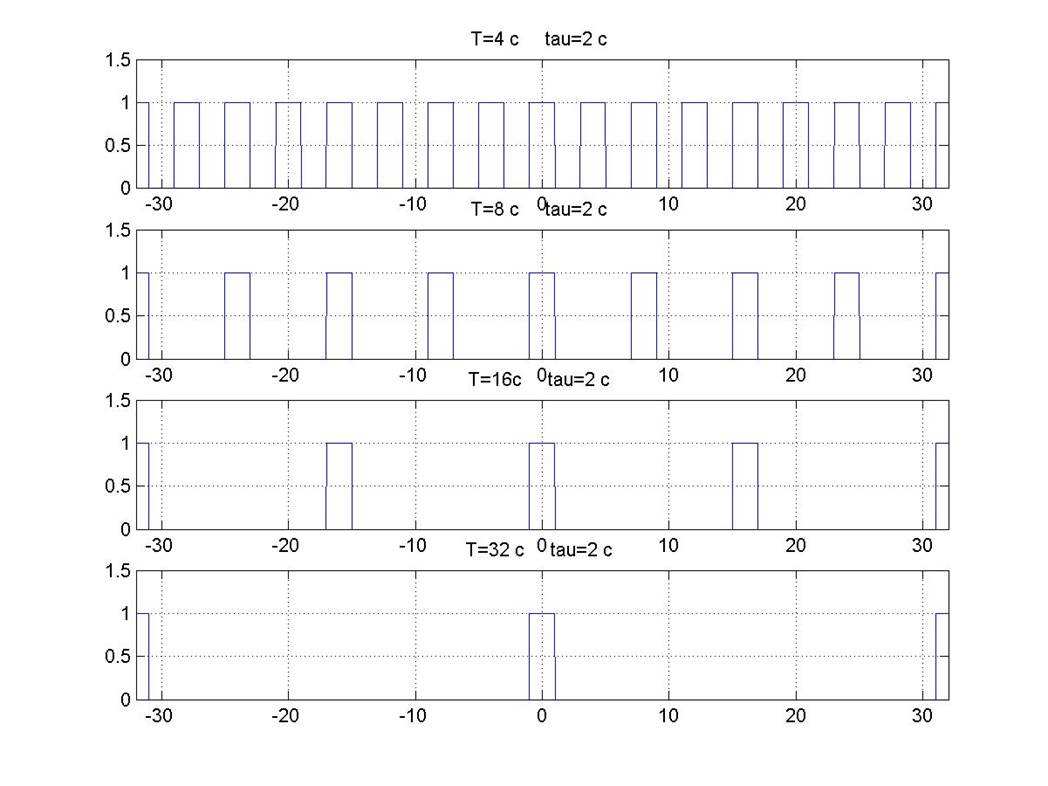
Рис. 1
pulstran(…) –это функция генерирующая последовательности из конечного числа импульсов, форма которых задается непрерывными функциями или наборами отсчетов.
Из полученных графиков четко видно, что число импульсов, при постоянной их длительности, на одном и том же интервале времени уменьшается с увеличением периода.
Задание
№2:Используем
функцию sinc(x) Matlab, для нахождения коэффициентов ряда Фурье. Построим
графики зависимостей амплитудных спектров сигналов от значений аргумента 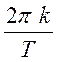 . Пронаблюдаем
за поведением спектра периодической последовательности прямоугольных импульсов
при изменении периода.
. Пронаблюдаем
за поведением спектра периодической последовательности прямоугольных импульсов
при изменении периода.
Файл-сценарий для построения графиков амплитудных спектров сигналов:
k=input('Введите число гармоник k = ');
x=-k:1:k; % задание интервала амплитудного спектра и числа гармоник
figure(1);
T1=4; %значение периода
x1=2*x/T1; %значение аргумента
y1=2/T1*sinc(x1); %использование функции sinc
T2=8;
x2=2*x/T2;
y2=2/T2*sinc(x2);
T3=16;
x3=2*x/T3;
y3=2/T3*sinc(x3);
T4=32;
x4=2*x/T4;
y4=2/T4*sinc(x4);
%Построение графиков
subplot(4,1,1),stem(x,abs(y1)),title('T=4'),grid on
subplot(4,1,2),stem(x,abs(y2)),title('T=8'),grid on
subplot(4,1,3),stem(x,abs(y3)),title('T=16'),grid on
subplot(4,1,4),stem(x,abs(y4)),title('T=32'),grid on
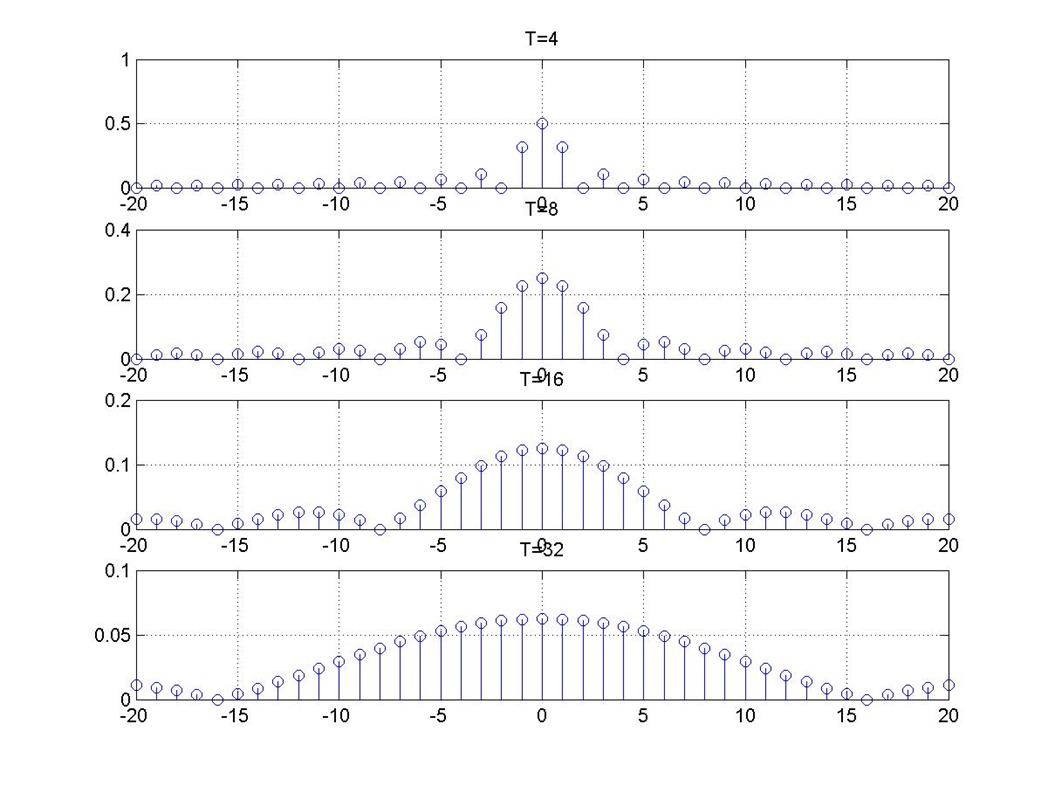
Рис. 2
y=sinc(x) - это функция представляющая собой обратное непрерывное преобразование Фурье от прямоугольного импульса шириной (2*pi )и высотой 1:

Из полученных графиков видно, что с увеличением периода T спектр становится более “частым”, для непериодического сигнала частотный интервал ∆ω=2π/T→0 при T→∞. Огибающая спектра с ростом периода становится более плавной (сглаживается).
Задание №3:Определим аналитическим путём прямое преобразование Фурье для сигнала, заданного в приложении 1. Построим графики амплитудного и фазового спектров сигнала.
![]() ,
,
![]()
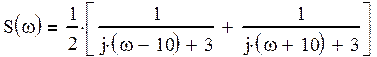
Определим аналитически прямое преобразование Фурье:
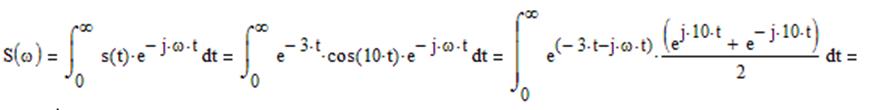
![]()
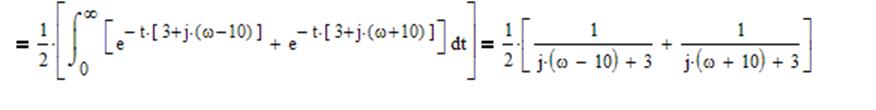
В результате получим:
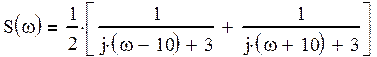
Что сходится с заданием.
Файл-сценарий для построения графиков амплитудного фазового спектров сигнала (Приложение № 2 методических указаний):
T=10;dt=0.1; % задание интервала времени
t=0:dt:T;
s = exp(-3*t).*cos(10*t);% определение функции
df=1/10; Fmax=1/dt; f=-Fmax:df:Fmax; % задание частотной шкалы
w=2*pi*f;
S=1/2.*(1./(j.*(w-10)+3)+1./(j.*(w+10)+3)); % выражение комплексного спектра
% построение графиков сигналов и спектров
subplot(311), plot(t,s), title('Cигнал')
subplot(312), plot(f,abs(S)), title('Амплитудный спектр'),grid on
subplot(313), plot(f,angle(S)), title('Фазовый спектр'), grid on
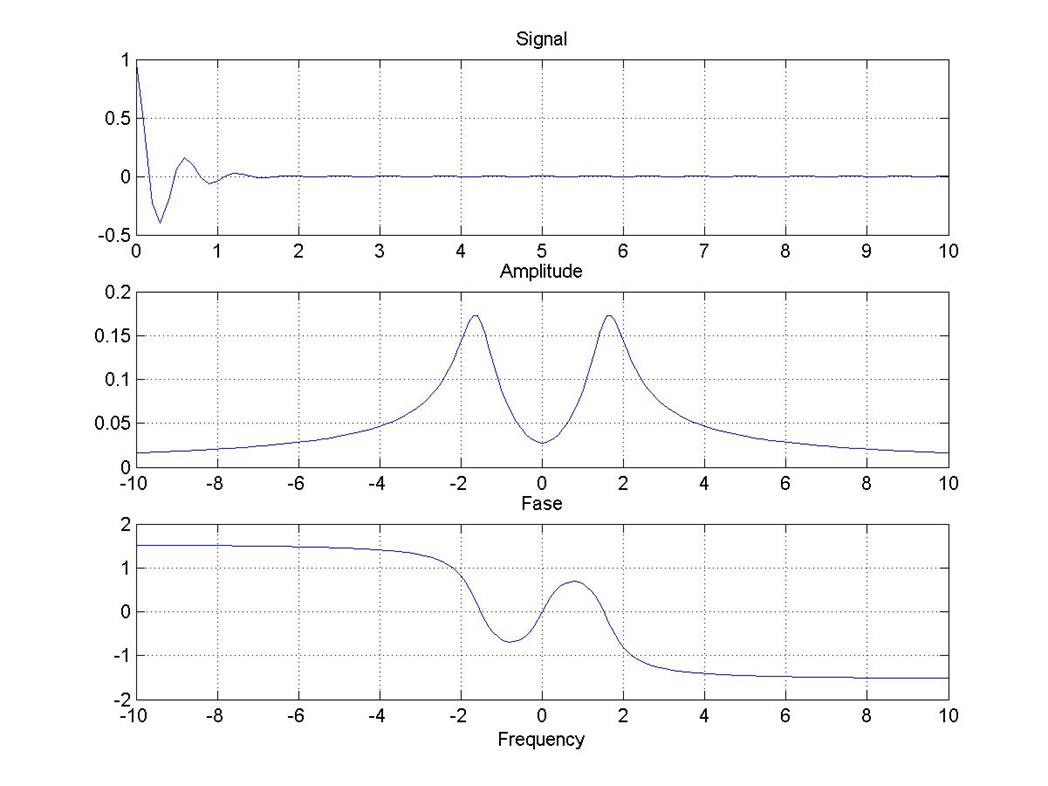
Рис. 3
Прямое преобразование Фурье исходного сигнала дает вполне соответствующие виды графиков амплитудного и фазового спектров сигнала. Из полученных графиков видно, что амплитудный и фазовый спектры непериодического сигнала имеют нечетную симметрию.
Задание №4:Напишем функцию (.m - файл) для вычисления дискретного преобразования Фурье:
function X=dftsum(x); % определение функции dftsum(x)
N=length(x); % вычисление количества точек, рассчитанных для исходного
% сигнала x
for n=0:1:N-1;
for k=0:1:N-1;
xk(k+1)=x(k+1)*exp(-j*2*pi*k*n./N); % формула для вычисления ДПФ
end
X(n+1)=sum(xk);
end;
Данная процедура дает линейную комбинацию отсчетов сигнала и приводит к дискретному преобразованию Фурье (ДПФ).
Задание №5:Вычислим с помощью функции dftsum(x), написанной в предыдущем пункте, ДПФ сигнала. Построим графики амплитудного и фазового спектров.
Файл-сценарий для построения графиков амплитудного фазового спектров сигнала с помощью процедуры dftsum()(Приложение № 3 методического указания):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.