НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра ССОД
Лабораторная работа № 2
«спектральные представления непрерывных периодических сигналов»
Выполнил студент:
Факультет: АВТ
Гр.: АИ-22
Серебрянников В.Н.
Вариант: 3
Преподаватель:
Доц. Щетинин Ю.И.
НОВОСИБИРСК 2004г.
Цель работы: изучение понятия спектра периодического сигнала, приобретение практических навыков вычисления и построения графиков спектров сигналов в среде MATLAB.
Задан сигнал по графику:
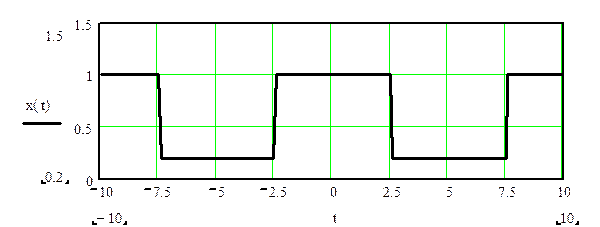
Аналитически найдём коэффициенты разложения в комплексный ряд Фурье данного сигнала:
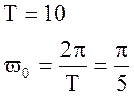
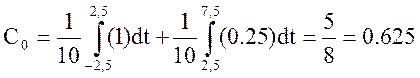
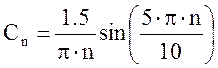
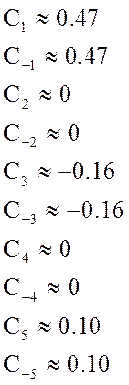
Ряд Фурье:
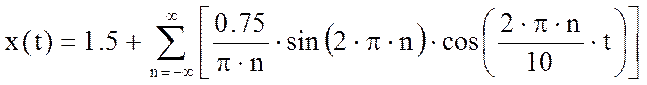
График амплитудного спектра сигнала:
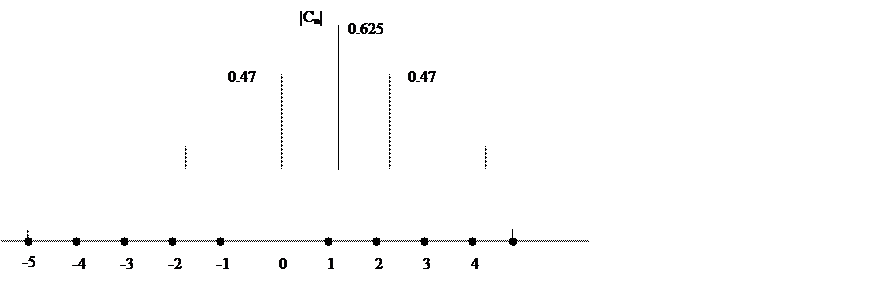 |
Программа, отображающая амплитудный и фазовый спектр:
T=10.0;
A=0.75;
t=5.0;
n1=1:15;
cn=(2*A./(pi.*n1)).*sin(pi.*n1.*t/T);
n2=-15:-1;
c_n=(2*A./(pi.*n2)).*sin(pi.*n2.*t/T);
Cn=[c_n 0.625 cn];
n3=[n2 0 n1];
n=-15:15;
figure(1), subplot(121),stem(n,abs(Cn))
title('|Cn|')
subplot(122),stem(n,angle(Cn))
title('angle(c_n) in rad')
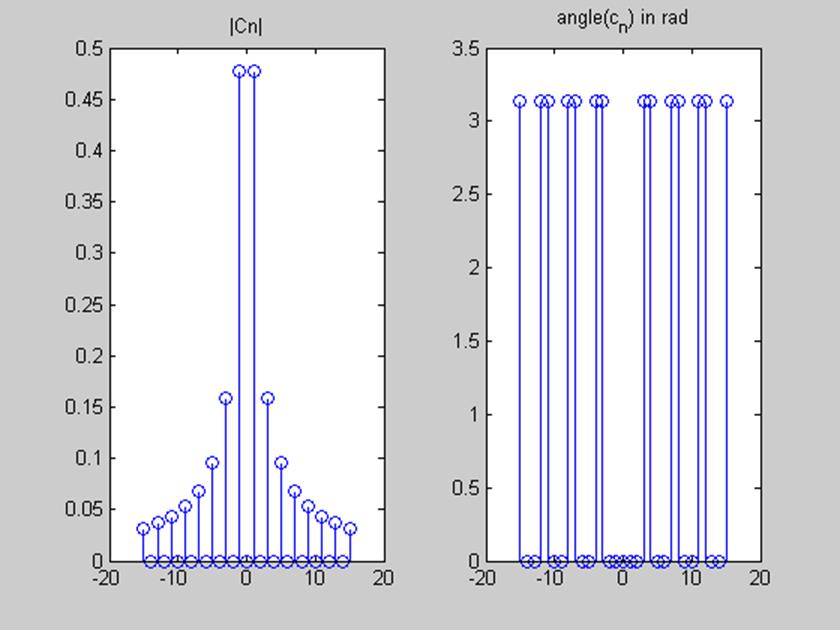
Рис. 2. «Амплитудный и фазовый спектр»
4. Определим коэффициенты ряда Фурье с помощью функции fft() пакета Matlab.
Для этого составим скрипт-файл:
t=0:T/63:T;% временной интервал
x=rectpuls(t,5)+0.25*rectpuls(t-5,5)+rectpuls(t-10,5);% генерирование сигнала
figure(1);
subplot(311), plot(t,x) % график сигнала
title('Signal')
k=0:63;
% коэффициенты ряда Фурье
C=(1.5./(pi.*k)).*sin(pi.*k.*5/10);
% график амплитудного спектра
subplot(312),
stem(2*pi*k/T, abs(C));
title('Amplitude spectrum of a signal')
y=fft(x,64);% Дискретное преобразование Фурье сигнала
% график ДПФ
subplot(313), stem(2*pi*k/T, abs(y)/64);
xlabel('Angular frequency, rad/sec');
title('Amplitude spectrum of a signal on procedure fft');
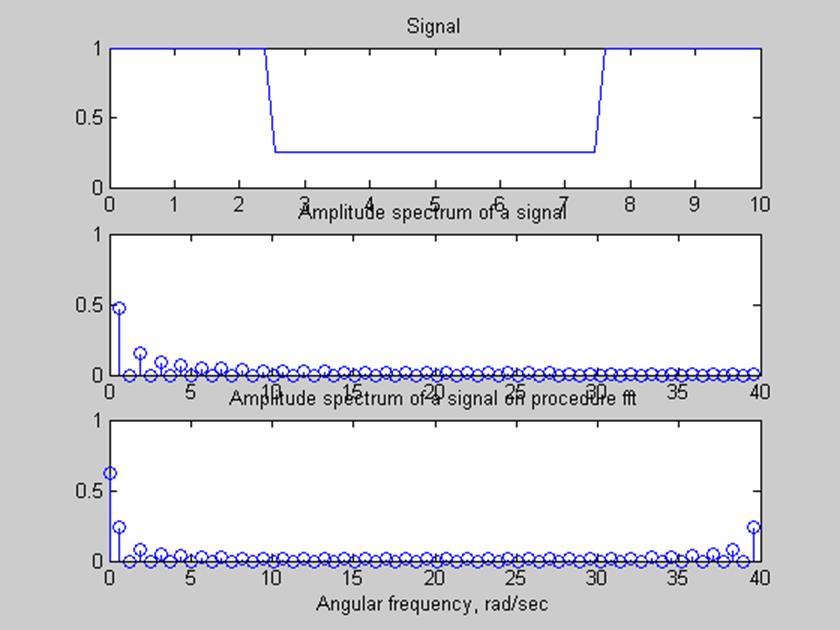
Рис.3 «Определение коэффициентов ряда Фурье с помощью пакета Matlab»
5. Исследуем ряд Фурье на сходимость. Для этого составим программу для вывода графического представления гармоник при их различном количестве.
T=10; %Период сигнала
w0=2*pi/T;%Угловая частота основной гармоники
t=-1.5*T:T/1000:1.5*T;%временной интервал
N=input('Number of harmonics ');
c0 = 5/8;
x=c0*ones(1,length(t)); % dc component
for k=1:N,
ck =(0.75./(pi.*k)).*sin(pi.*k.*5/10); ;
cn = conj(ck);
x = x + ck.*exp(j*k*w0*t) + cn.*exp(-j*k*w0*t);
end
figure(2)
plot(t,x)
title(['N = ',num2str(N)])
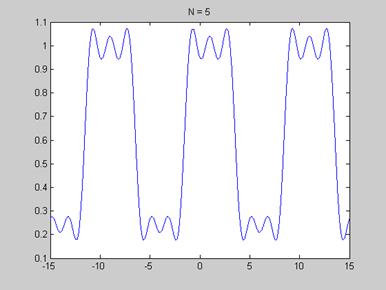
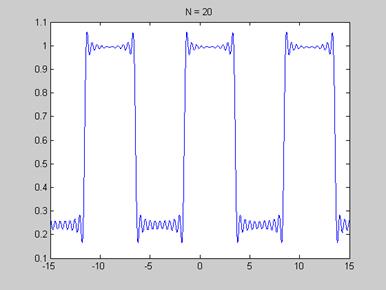
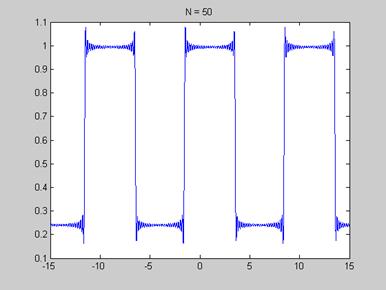
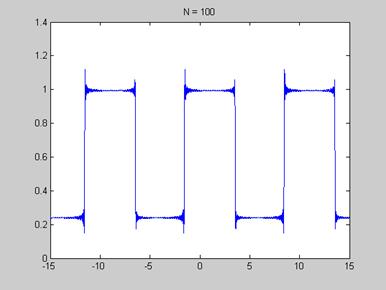
Рис. 4. «Создание сигнала с помощью разного количества гармоник»
Из рисунков видно, что при увеличении числа гармоник сигнал стремиться к прямоугольному.
6. Выполним синтез периодического сигнала с помощью пакета Simulink.
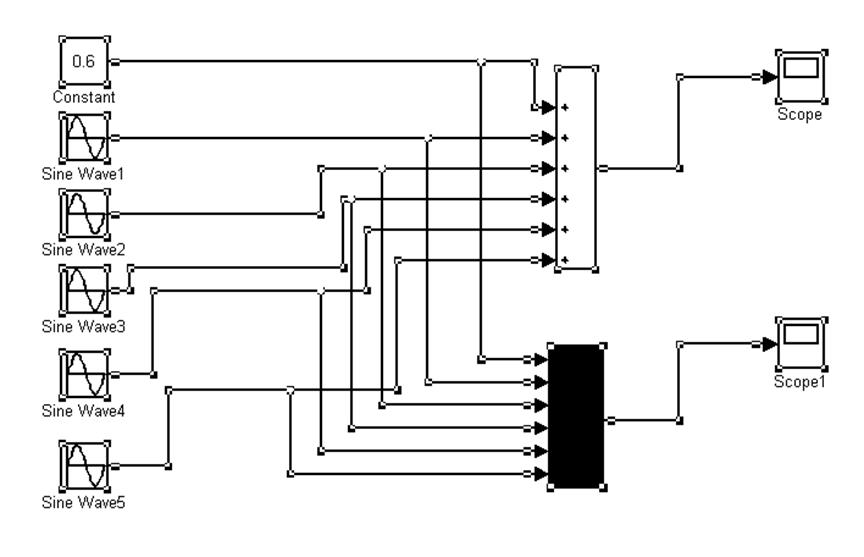
Рис. 5. «Схема формирования сигнала из отдельных гармоник»
В результате на осциллографе с сумматора мы увидим сигнал:
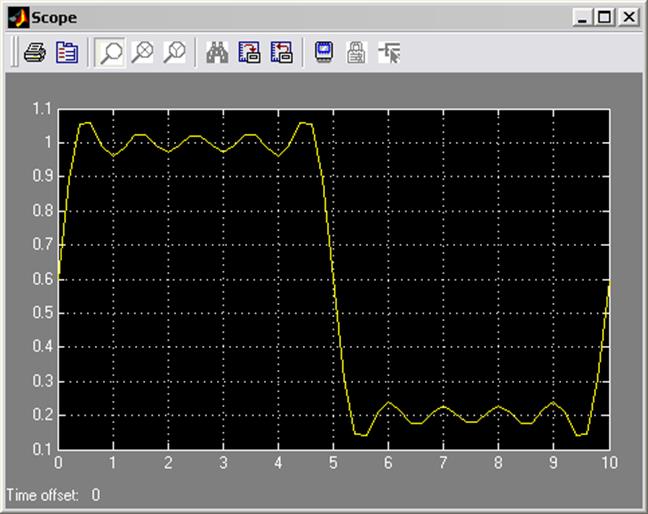
Рис. 6. «Суммарный импульс, составленный из нескольких гармоник»
На осциллографе с мультиплексора будет изображена каждая из гармоник-составляющих:
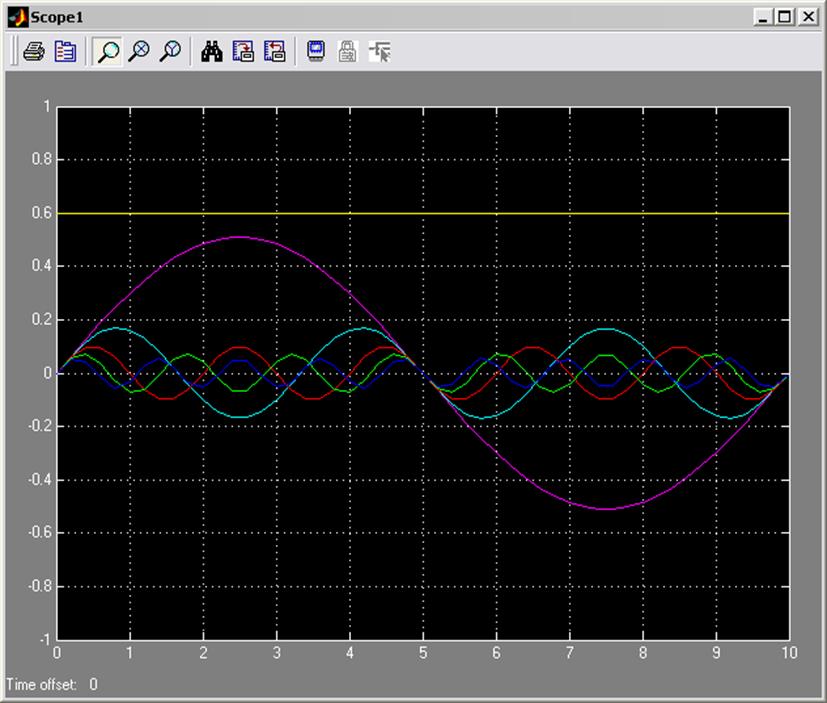
Рис. 7. «Отельное изображение каждой из гармоник»
Вывод: в ходе лабораторной работы мы изучили методы разложения сигнала в ряд Фурье на гармоники, а так же суммирование гармоник для получения сигнала.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.