НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
ЛАБОРАТОРНАЯ РАБОТА № 2
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ НЕПРЕРЫВНЫХ
ПЕРИОДИЧЕСКИХ СИГНАЛОВ
Cтудент: Габриэлян А. Преподаватель:
Факультет: АВТ Доц. Ю. И. Щетинин
Группа АТ-33
Новосибирск
2005
Цель работы:изучение понятия спектра периодического сигнала, приобретение практических навыков вычисления и построения графиков спектров сигналов в среде MATLAB.
1. Получение
аналитически коэффициентов разложения в комплексный ряд Фурье данного сигнала.
Построение графиков амплитудного и фазового спектров сигнала. 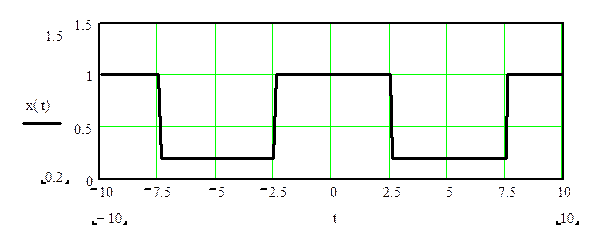
Рис.1 График сигнала
Ряд
Фурье 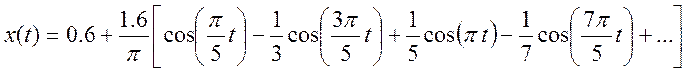
В данном варианте задания дан спектр периодической последовательности прямоугольных импульсов, которая широко используется в системах различного назначения.
Найдем коэффициенты Фурье данного сигнала
Частота основной гармоники 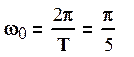 ,
T=10
,
T=10
Функция: 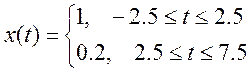
Коэффициенты комплексного ряда Фурье
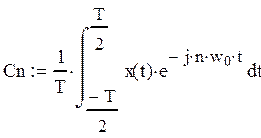 .
.
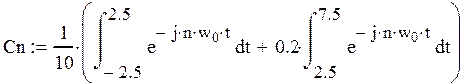
![]()
|
|
|
|
|
|
|
|
|
|
|
|
Для n = 0
|
|
|
|
В частности,
|
C1=0.255 |
|
C2=0 |
|
C3=0.085 |
|
C4=0 C5=0.051 |
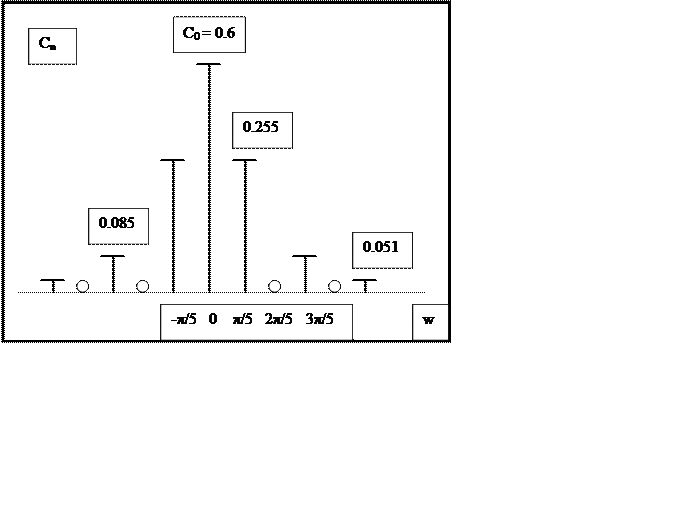
Рис.2 График амплитудного спектра сигнала
Так как функция сигнала непрерывная, то амплитуды гармоник пропорциональны (1/k2).
Фазовый спектр данного сигнала нулевой, т.к. функция
четная и bk =0,а![]() , отсюда следует
, отсюда следует ![]() .
.
2. Написание и выполнение файла-сценария , позволяющего построение графиков амплитудного и фазового спектров сигнала
n1=1:15;
cn=sin(pi/2.*n1)./(pi*n1).*(1+0.2.*exp(-j*pi*n1));
n2=-15:-1;1
c_n=sin(pi/2.*n2)./(pi*n2).*(1+0.2.*exp(-j*pi*n2));
Cn=[c_n 0.6 cn];
n3=[n2 0 n1];
n=-15:15;
figure(1), subplot(121),stem(n,abs(Cn))
title('|Cn|')
subplot(122),stem(n,angle(Cn))
title('angle(c_n) in rad')
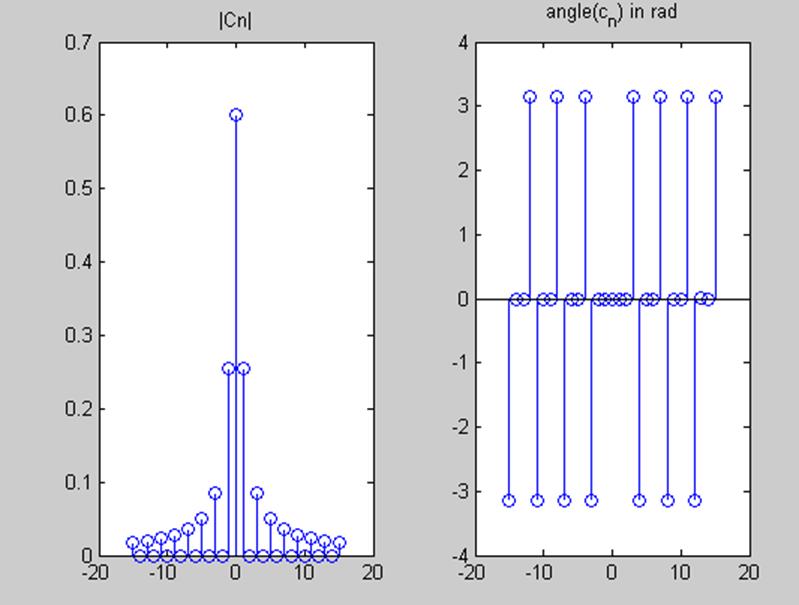
Рис.3 Амплитудный и фазовый спектр сигнала
В данном сценарии была использована команда angle – возвращает фазу в радианах ,матрицы состоящей из комплексных элементов.
3. Определение спектра Фурье сигнала с помощью функции fft() Matlab. Определение коэффициентов ряда Фурье для сигнала, заданного в п.2, с помощью fft(), построение и сопоставление графиков амплитудного спектра по п.2 и п.3.
T=10; % период сигнала
t=-T:T/63:T; % временной интервал
x=0.2+0.8*rectpuls(t-0,5)+0.8*rectpuls(t-10,5)+0.8*rectpuls(t+10,5); % генерирование сигнала
figure(1);
subplot(311), plot(t,x) % график сигнала
title(' Graphic of signal')
axis([-10 10 0 1.5])
k=0:63;
% коэффициенты ряда Фурье
C= sin(pi/2.*k)./(pi*k).*(1+0.2.*exp(-j*pi*k));
% график амплитудного спектра
subplot(312),
stem(2*pi*k/T, abs(C));
title('|Cn|')
y=fft(x,64);% Дискретное преобразование Фурье сигнала
% график ДПФ
subplot(313), stem(2*pi*k/T, abs(y)/64)
xlabel('Angle(c_n) in rad')
title('|Cn| with proceed fft')
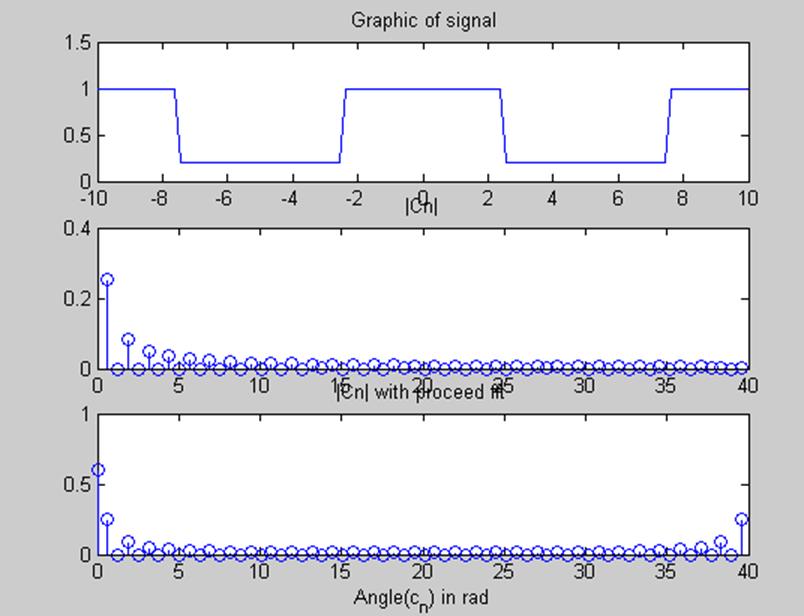
Рис. 4- Сигнал, амплитудный спектр и угловая частота.
fft(Х)- это дискретное преобразование Фурье вектора Х.Для матриц ,процедура fft применяется к каждому столбцу. Для массива размерностью N-D данная процедура на первом не одноэлементном множестве.
Результаты данного пункта демонстрируют сходство графика амплитудного спектра, полученного при аналитическом построении, и графика этого спектра, построенного с помощью встроенной функции MatLab – fft().
4. Составление и выполнение файла-сценария для исследования сходимости ряда Фурье к исходному периодическому сигналу. Ознакомление со сходимостью ряда для четырех значений числа членов ряда и с явлением Гиббса.
T=10;
w0 = 2*pi/T;
t = -1.5*T:T/1000:1.5*T;
N = input('Number of harmonics ');
c0 = 0.6;
x = c0*ones(1,length(t)); % dc component
for n=1:N,
cn = sin(pi/2.*n)./(pi*n).*(1+0.2.*exp(-j*pi*n));
c_n = conj(cn);
x = x + cn*exp(j*n*w0*t) + c_n*exp(-j*n*w0*t);
end
figure(2), plot(t,x), grid
title(['N = ',num2str(N)])
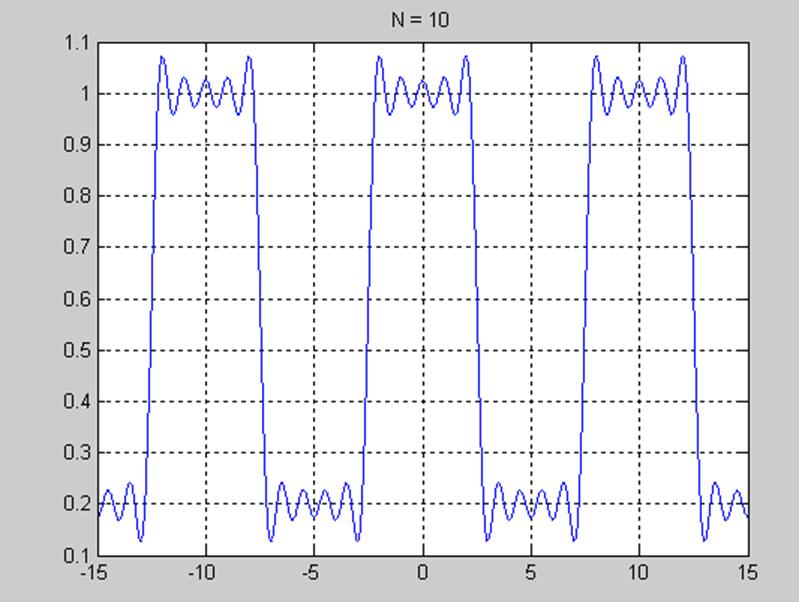
Рис.5 График приближения сигнала при значении N=10
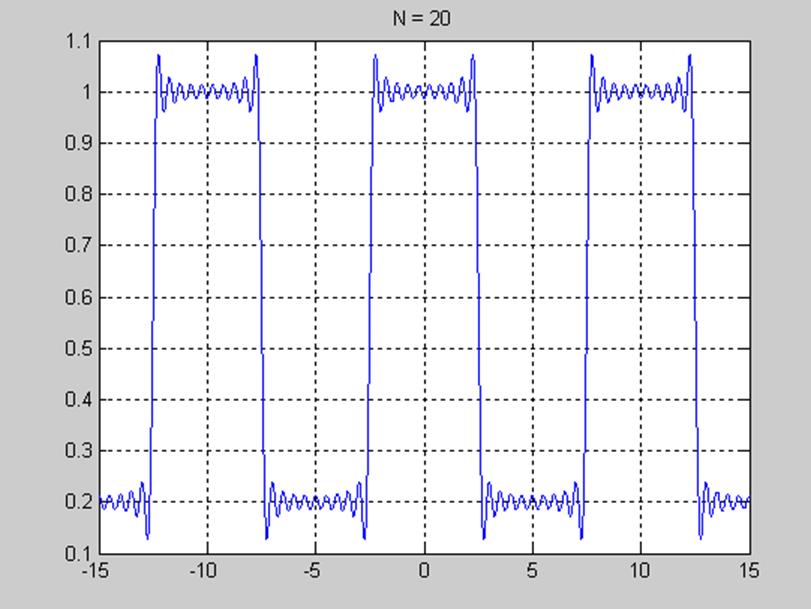
Рис.6 График приближения сигнала при значении N=20
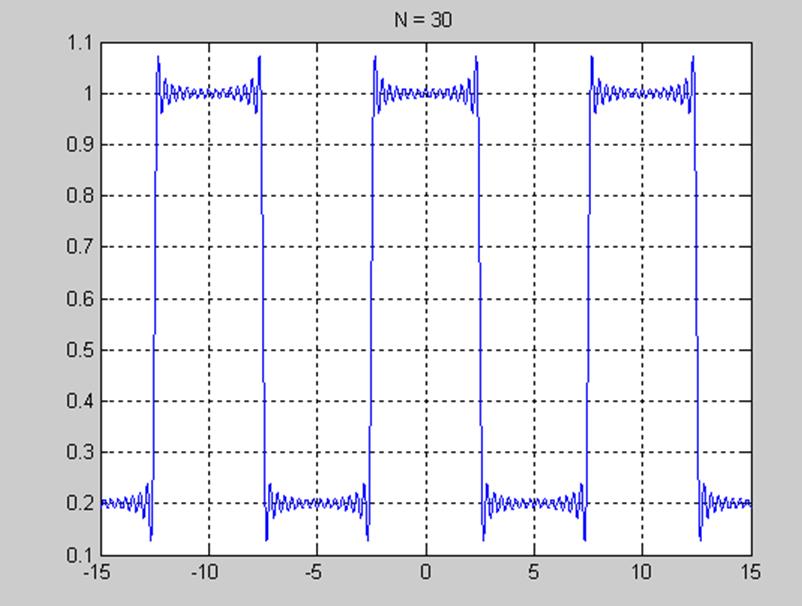
Рис.7 График приближения сигнала при значении N=30
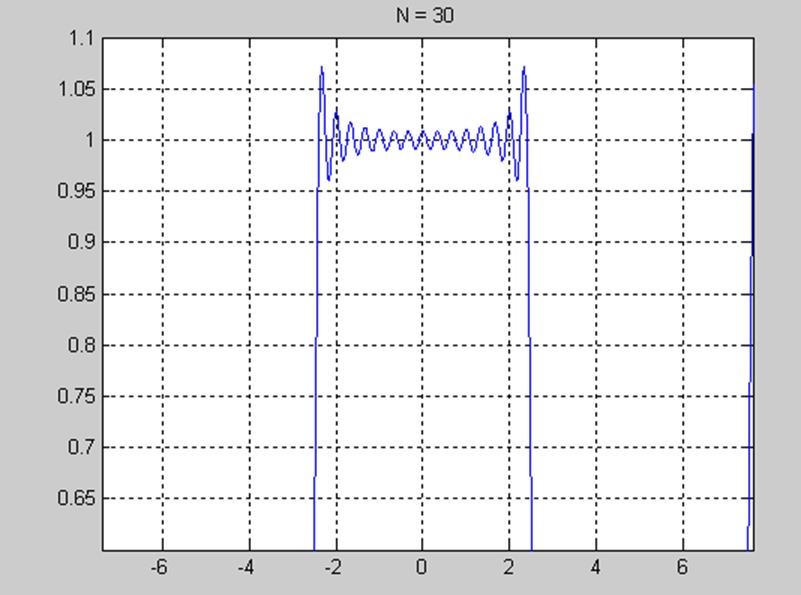
Рис.8 График приближения сигнала при значении N=30 (увелич.)
Явление Гиббса – это явление, связанное с появлением пульсаций при суммировании рядов Фурь
Можем сделать вывод ,что при увеличении числа членов ,пульсации становятся более узкими , но амплитуда их не уменьшается.
5. Выполнение задачи синтеза периодического сигнала, заданного в индивидуальном задании (п.2), с использованием пакета Simulink.
Построим модель Фурье-синтеза сигнала:
Графики синтеза сигнала с параметрами: амплитуда =3, частота = pi/8, 2*pi/8, 3*pi/8, 4*pi/8, 5*pi/8.
Рис. 9 - Вид S - модели Фурье-синтеза сигнала
Рис. 10 - График всех сигналов через сумматор.
Рис.11 График всех сигналов через мультиплексор.
Вывод: убеждаемся в том ,что при увеличении числа суммирующихся членов ряда Фурье, пульсации становятся более узкими.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.