Спектральные представления непрерывных непериодических сигналов: Методические рекомендации по выполнению лабораторной работы, страница 2

% Вычисление спектра и построение его графиков

T=10; dt=1/10;                                % Определение интервала времени

df=1/10; Fmax=1/dt;                           % Определение частотной шкалы

f=-Fmax/2:df:Fmax/2;           

t=0:dt:T;

s=exp(-3*t).*cos(10*t);  % Задание сигнала

y1=dftsum(s); y1p=fftshift(y1);              % Вычисление и сдвиг ДПФ

% Построение графиков сигнала и его спектров

figure(1)

subplot(311), plot(t,s),title('График сигнала');

subplot(312), plot(f,abs(y1p)),title('Амплитудный спектр')

grid on

subplot(313), plot(f,angle(y1p)), title('Фазовый спектр')

grid on

xlabel('частота')

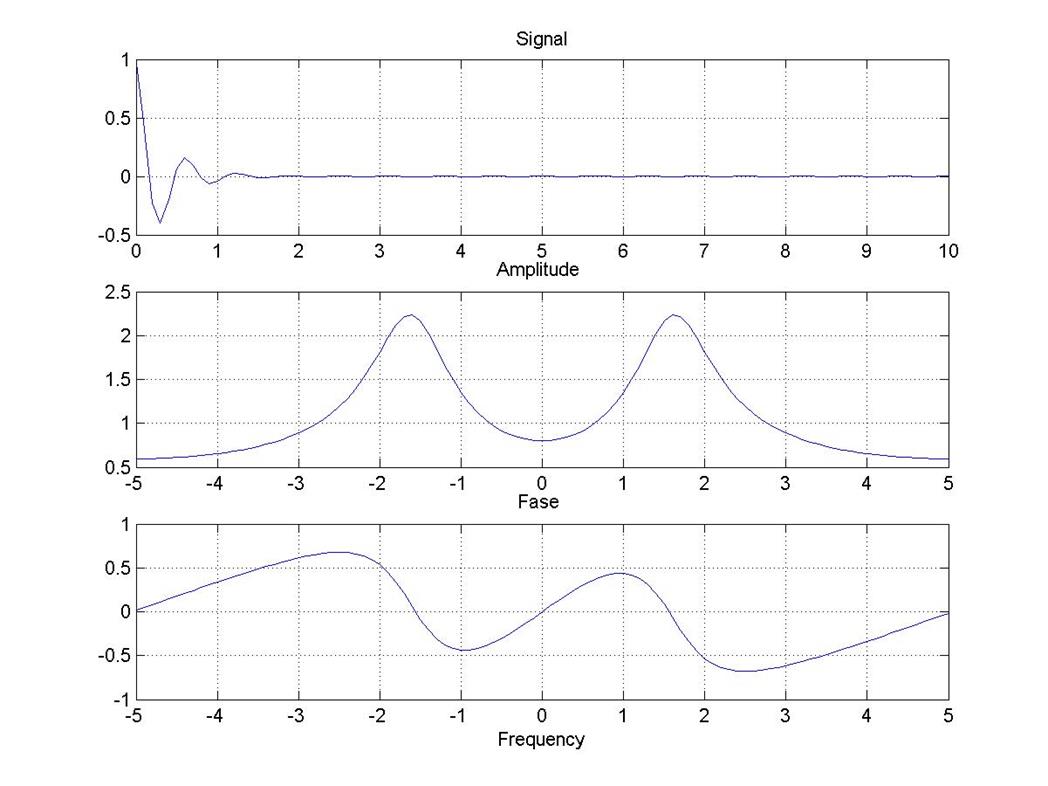
Рис. 4

Видим, что амплитудный спектр, полученный с использованием процедуры ДПФ dftsum(), аналогичен спектру построенному ранее. Так как dftsum() выдает результаты коэффициентов в комплексном виде, то фазовый спектр, полученный в данном пункте, отличается от спектра полученного в пункте 3.      

Задание №6: Проведём вычисления и построение графиков спектров сигнала с помощью функции  fft().

Файл-сценарий для построения графиков спектров сигнала с помощью процедуры fft()(Приложение № 4 методических указаний):

figure(2)

T=8;                    % длительность  процесса

% Процедура сопоставления преобразования Фурье

% и его вычисления с помощью функции fft()

N=128;                        % число точек                     

Ts=T/(N-1);                   % интервал отсчетов               

t=0:Ts:T;                  % временной интервал                 

s=exp(-3*t).*cos(10*t);  % генерирование импульса      

Fmax=1/Ts;                    % максимальная частота                  

df=1/T;                       % частотное разрешение                  

f=-Fmax/2:df:Fmax/2;          % частотная шкала

X=fft(s,N);              % БПФ сигнала         

Xp=fftshift(X);                % частотный сдвиг

A=abs(Xp);

w=2*pi*f;

S=1/2.*(1./(j.*(w-10)+3)+1./(j.*(w+10)+3));    % преобразование Фурье сигнала

% Построение графиков сигнала и амплитудных спектров

subplot(311),plot(t,s),title('График сигнала');

% график сигнала

subplot(312), plot(f,A*Ts),grid on

title('Амплитудный спектр сигнала по fft')

subplot(313), plot(f, abs(S)),grid on

xlabel('Частота')

title('Амплитудный спектр сигнала')

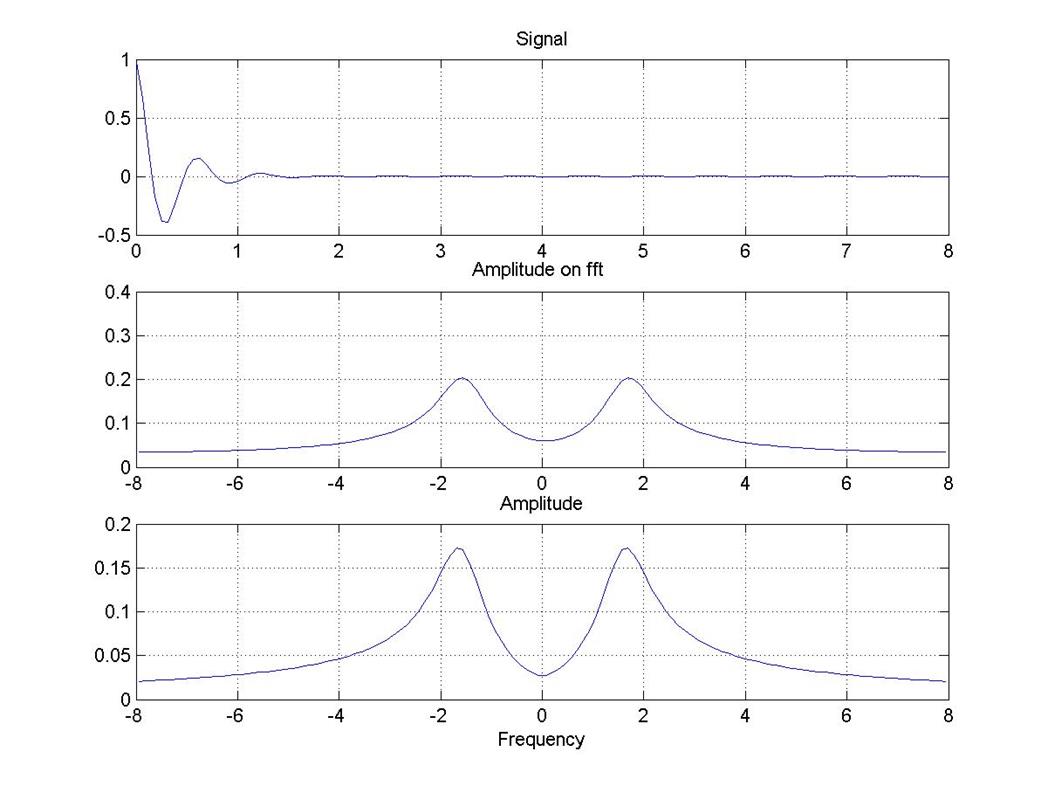
Рис. 5

Y=fftshift(X) - это функция, которая перегруппировывает выходные массивы функций, размещая нулевую частоту в центре спектра.

fft(Х) -это дискретное преобразование Фурье вектора Х.Для матриц ,процедура fft() применяется к каждому столбцу. Для массива размерностью N-D данная процедура  применяется на первом не одноэлементном множестве.

Из графиков видно, что амплитудные спектры, полученные с помощью разных процедур, отличаются не значительно. Первый из них построен с помощью функции  fft() MatLab 6.0, а второй с использованием аналитических выкладок.

Задание №7: Произведём изучение свойств преобразования Фурье.

Файл-сценарий для иллюстрации свойств преобразования Фурье (Приложение № 5 методических указаний):

% Процедура иллюстрации свойств преобразования Фурье

N = 128; %  Длина сигналов

k = 0:N-1;

gamma = -0.5;

g = exp(gamma*k);% g - экспоненциальная функция

h = sin(2*pi*k/(N/2));

figure(1)

plot(k,g,k,h),grid on

% h - синусоидальная последовательность с периодом = N/2

% вычисление преобразований Фурье сигналов

[G,w] = freqz(g,1,512);

[H,w] = freqz(h,1,512);

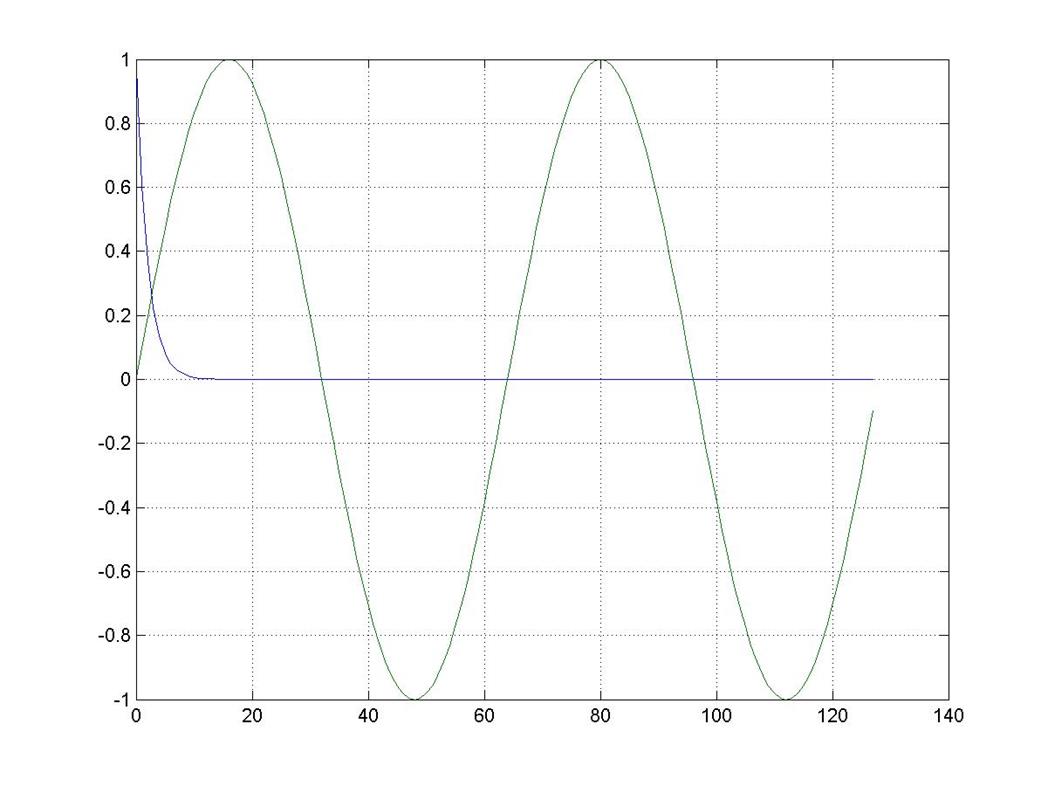
Рис. 6

% Свойство линейности

alpha = 0.5;

beta = 0.25;

y = alpha*g+beta*h;

[Y,w] = freqz(y,1,512);

% Графики Y и  alpha*G+beta*H для проверки их равенства

figure(2), subplot(211),plot(abs(Y)),grid on

subplot(212), plot(abs(alpha*G+beta*H)),grid on

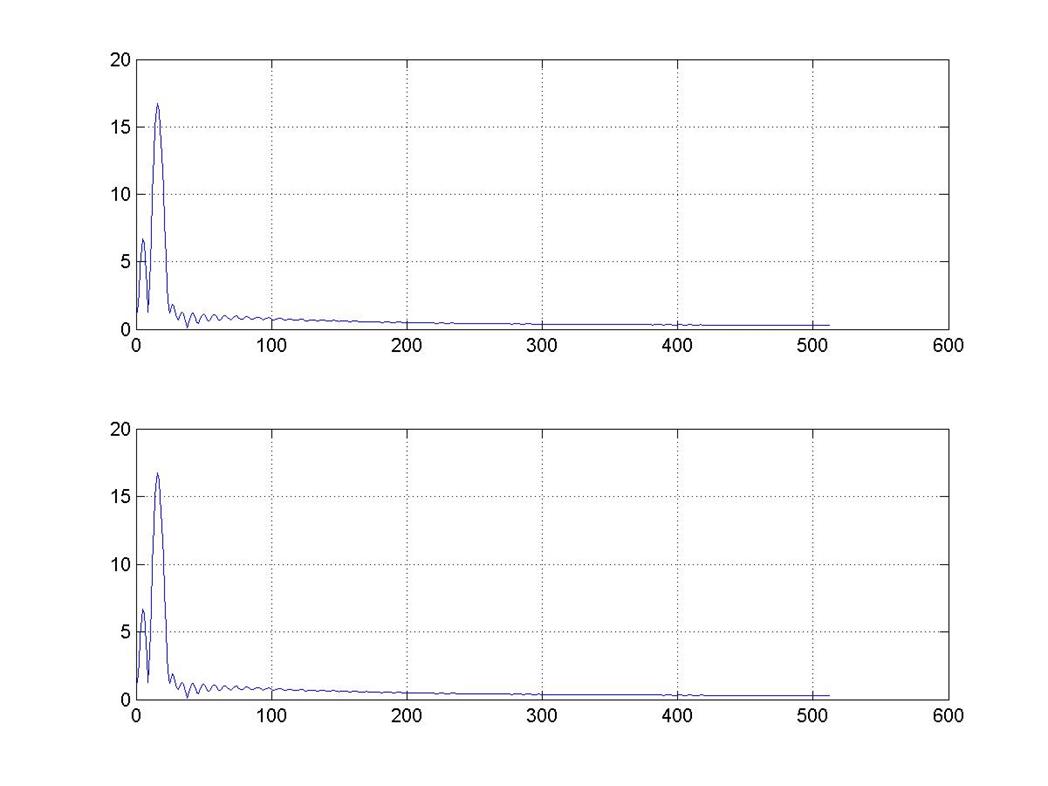
Рис. 7

Из графиков видно, что спектр суммы равен сумме спектров исходных сигналов

% Свойство временного сдвига

n0 = 12; % y2 - последовательность y, сдвинутая на 12 отсчетов

y2 = [zeros([1,n0]) g];

[Y2,w] = freqz(y2,1,512);

G0 = exp(-j*w*n0).*G;

% Графики амплитудных спектров

figure(3)

subplot(211),plot(abs(G0)),grid on

subplot(212),plot(abs(Y2)),grid on

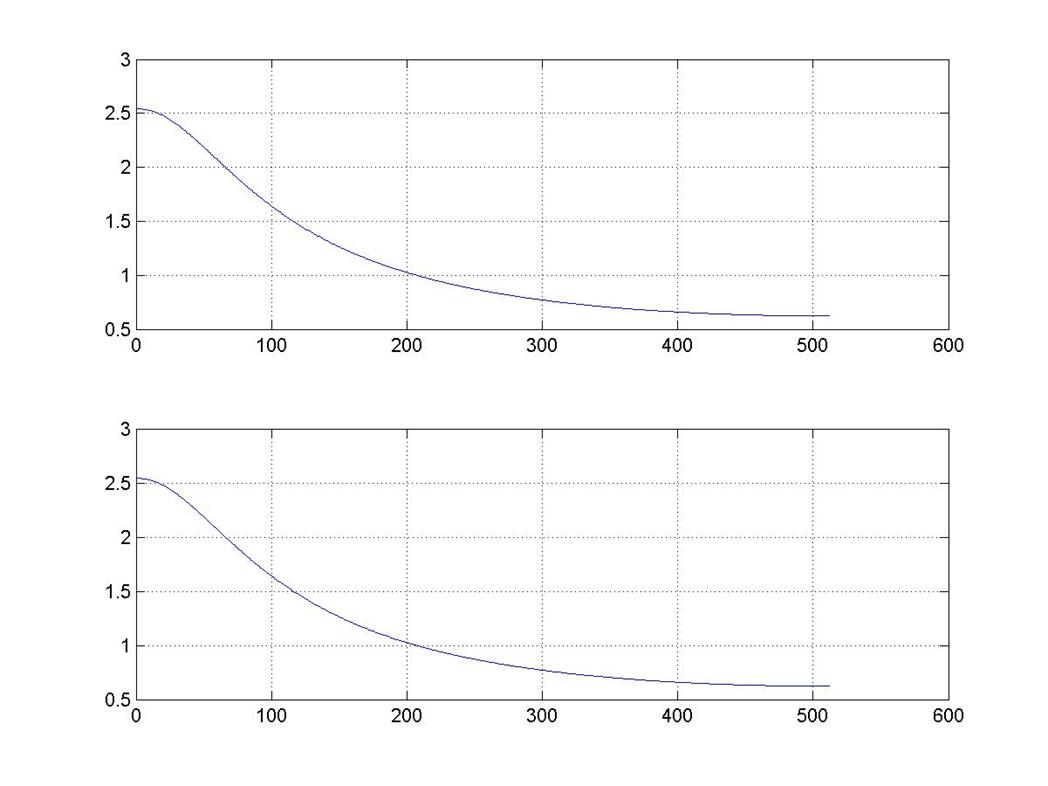
Рис. 8

Из полученных графиков видно, что при осуществлении временного сдвига амплитудный спектр сигнала не меняется.

% Свойство изменения масштаба

a=0.1; % Коэффициент изменения масштаба

g1= exp(gamma*k*a);

% Графики во временной области

figure(4)

plot(k,g,k,g1),grid on

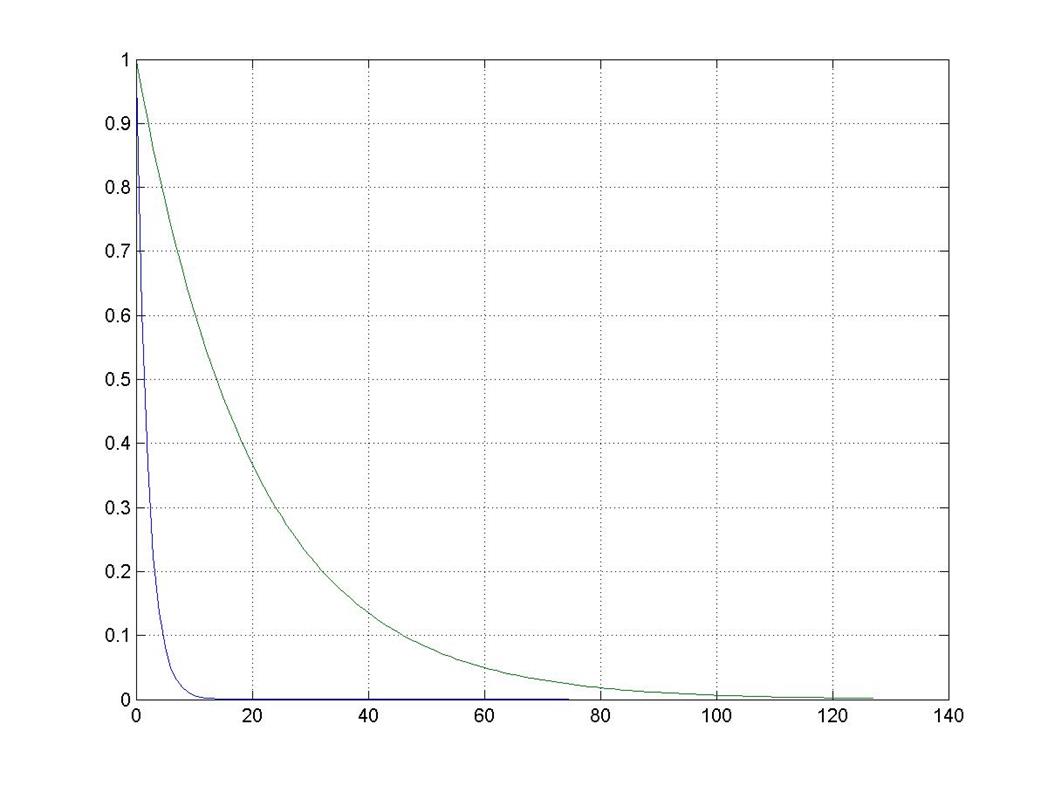
Рис. 9

При данном изменении масштаба скорость спада (убывания) экспоненциальной зависимости уменьшается.

[G,w] = freqz(g,1,512);

G1 = freqz(g1,1,512);

% Графики спектров

figure(5)

subplot(211),plot(w',abs(G)),grid on

subplot(212),plot(w,abs(G1)),grid on

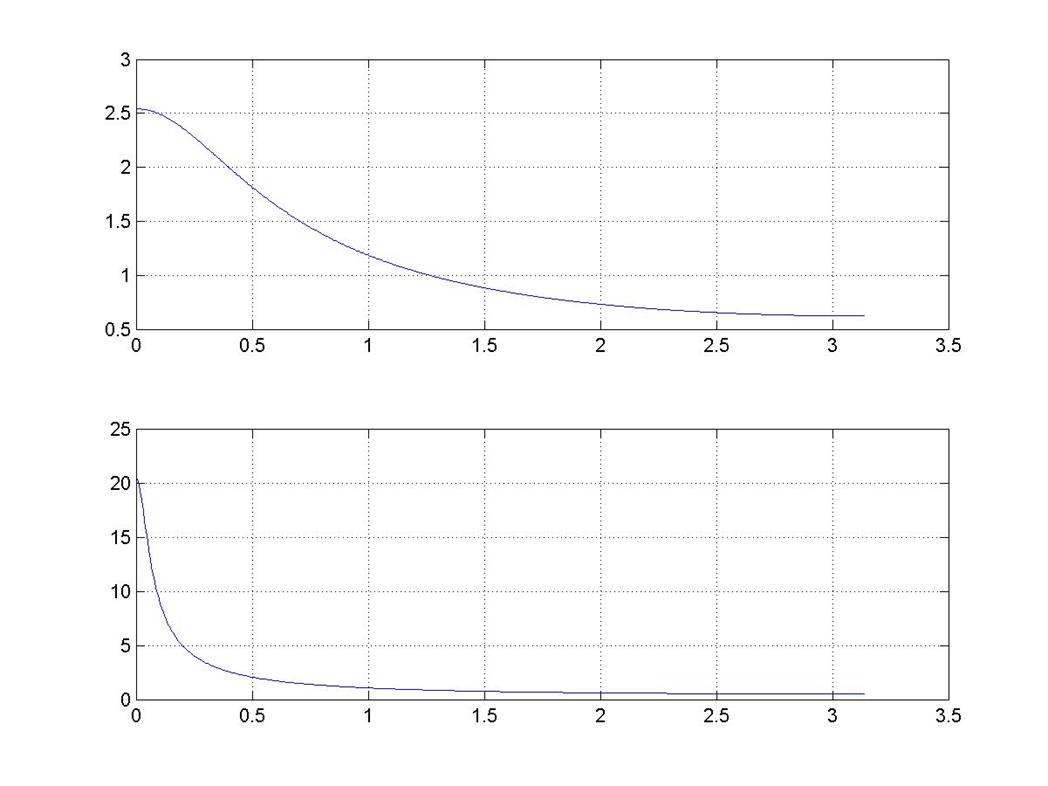
Рис. 10

По графику видно, что изменение длительности сигнала приводит к изменению огибающей спектра.

% Свойство свертки

y5 = conv(g,h);

[Y5,w] = freqz(y5,1,512);

% Графики спектров

figure(6)

subplot(211),plot(abs(Y5)),grid on

subplot(212),plot(abs(G.*H)),grid on

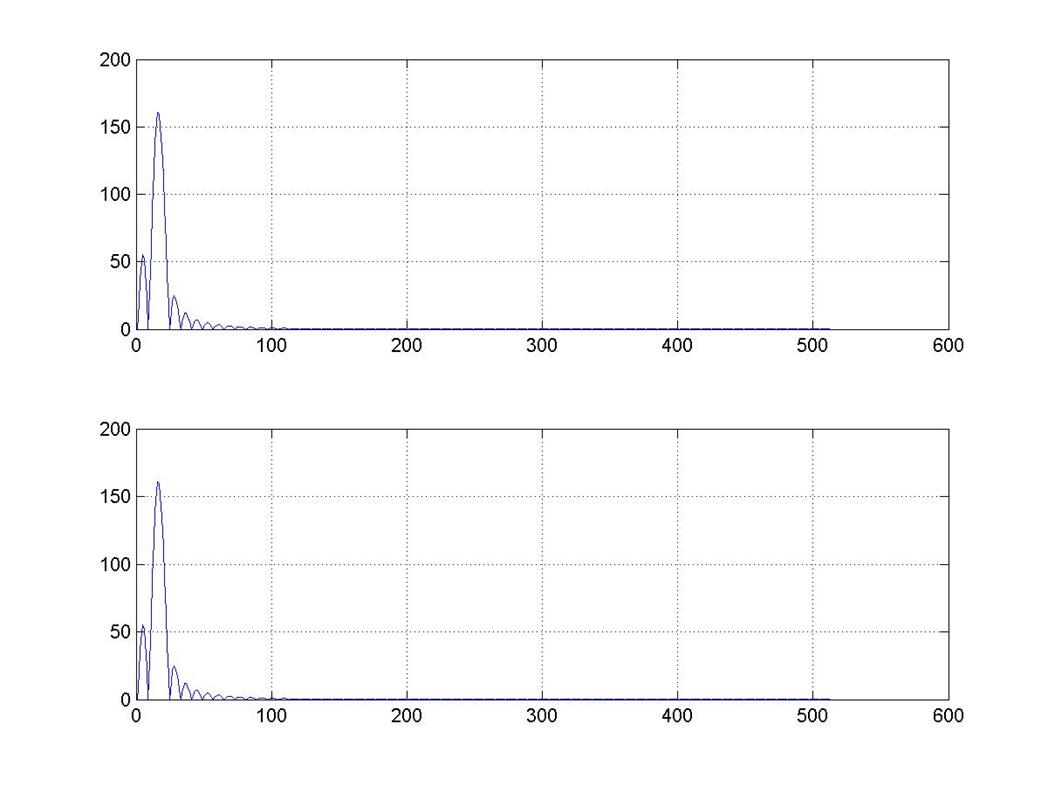
Рис. 11

Свойство свертки показывает, что спектр свертки равен произведению спектров сигналов.

% Теорема Парсеваля

H0 = exp(-j*w*n0).*H;

val1 = sum(g.*conj(h));

val2 = sum(G0.*conj(H0))/512;

% Сравнение val1 с val2

disp('Разность   val1-val2 = '),disp(val1-val2)

Разность   val1-val2 = 0.0000 - 1.3618i

Выводы: В лабораторной работе по спектральным представлениям непрерывных непериодических сигналов мы изучили преобразование Фурье и его свойства. А так же понятия амплитудного и фазового спектров непрерывных во времени сигналов. В ходе работы были получены амплитудные спектры с помощью аналитических выкладок, с помощью написанной функции dftsum() и функции MatLab – fft(). Сравнив полученные результаты, можно сделать вывод о незначительном отличае в зависимости от используемого метода.

Литература:

1.  Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. пособие.- Новосибирск. Изд-во НГТУ,  1998 - ч.1.

2.   Голышев Н.В., Щетинин Ю.И. Задачник-практикум по теории и обработке сигналов.:      

       учеб. пособие. Новосибирск: Изд-во НГТУ, 2001