НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов», 5 - й семестр
ЛАБОРАТОРНАЯ РАБОТА № 3
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
Цель работы:Изучение преобразования Фурье и его свойств, понятий амплитудного и фазового спектров непериодических непрерывных во времени сигналов, приобретение практических навыков вычисления преобразования Фурье, построения графиков и анализа спектров в среде Matlab.
Задание и порядок выполнения работы
1. Ознакомьтесь с преобразованием Фурье, его свойствами, понятиями амплитудного и фазового спектров непериодического сигнала по учебной литературе, например, [1] стр. 28 – 43 или [2] стр. 31 – 49.
2. Используя функцию pulstran(…) Matlab сформируйте четыре четные последовательности прямоугольных периодических импульсов единичной амплитуды с параметрами
а) период Т = 1 с, длительность импульса ![]() τ = 0.25 с,
τ = 0.25 с,
б) период Т = 4 с, длительность импульса ![]() τ = 0.25 с,
τ = 0.25 с,
в) период Т = 8 с, длительность импульса ![]() τ = 0.25 с,
τ = 0.25 с,
г) период Т = 32 с, длительность импульса ![]() τ = 25 с.
τ = 25 с.
Постройте графики этих сигналов в одном графическом окне.
Используя функцию sinc(x) Matlab,
выразите с её помощью коэффициенты ряда Фурье прямоугольной периодической
последовательности. Обратите при этом внимание, что в Matlab ![]() , т.е. переменная x в sin(x)/x умножена на π.
, т.е. переменная x в sin(x)/x умножена на π.
Постройте
в одном графическом окне графики зависимостей амплитудных спектров сигналов из
п.2 от значений аргумента 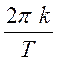 (k – номер
гармоники, Т – значение периода). Пронаблюдайте поведение спектра при
изменении периода и сделайте вывод о поведении плотности линий и огибающей
спектра при
(k – номер
гармоники, Т – значение периода). Пронаблюдайте поведение спектра при
изменении периода и сделайте вывод о поведении плотности линий и огибающей
спектра при ![]() .
.
Какой характер спектра можно предполагать для непериодического прямоугольного
импульса? Какое различие и связь между спектрами периодического и
непериодического сигналов?
3. Аналитически определите прямое преобразование Фурье для сигнала, заданного в индивидуальном задании, и постройте графики амплитудного и фазового спектров сигнала. Пример выполнения этого пункта приведен в Приложении 2.
4. Напишите функцию (.m - файл) вычисления дискретного преобразования Фурье (ДПФ) с синтаксисом
![]() ,
,
где x – N -точечный вектор значений x(0),…,x(N-1) сигнала и X- вектор значений ДПФ. В функции с использованием циклов for по n и k и встроенной функции sum() должно вычисляться ДПФ по формуле
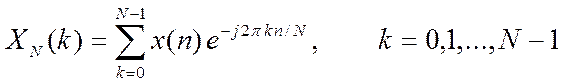 .
.
5. Вычислите с помощью функции dftsum(x) ДПФ сигнала, заданного в п.3, и постройте графики его амплитудного и фазового спектров. Соответствующий пример представлен в Приложении 3.
6. Ознакомьтесь со встроенной в Matlab функцией fft() для вычисления ДПФ по алгоритму быстрого преобразования Фурье (БПФ). Связь преобразования Фурье непрерывного времени (НВПФ) и дискретного преобразования Фурье (ДПФ) показана в Приложении 4.
С помощью функции fft() проведите вычисление спектра сигнала из индивидуального задания с масштабированием шкалы частот. Постройте в одном графическом окне графики амплитудного спектра, вычисленные в п. 3,5,6.
Для сопоставления результатов, возвращаемых fft(), со значениями
преобразования Фурье сигнала возвращаемые функцией fft() значения должны быть
промасштабированы, а именно 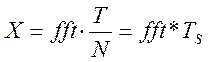 , где T – длительность анализируемого
сигнала, N – количество
точек, в которых определяется спектр, ТS - интервал
отсчетов. См. Приложение 4 и Приложение 5.
, где T – длительность анализируемого
сигнала, N – количество
точек, в которых определяется спектр, ТS - интервал
отсчетов. См. Приложение 4 и Приложение 5.
Пояснение. Чтобы применить процедуру fft() для представления сигнала в частотной области с
соответствующим масштабированием шкалы частот необходимо
§
по значению интервала отсчетов 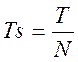 (Т – длительность сигнала, с)
определить максимальную частоту анализа Fmax (в
герцах) по формуле
(Т – длительность сигнала, с)
определить максимальную частоту анализа Fmax (в
герцах) по формуле
![]() ,
,
§
найти частотное разрешение, т.е. минимальное
расстояние между частотами в частотной области
![]() ,
,
§ провести вычисления с помощью fft(),
§ применить процедуру fftshift(), которая переставляет местами первую и вторую половину частотного спектра, возвращаемого fft(),.
§
сформировать вектор значений
частот по выражению ![]() .
.
§ построить график амплитудного и/или фазового спектра сигнала в зависимости от частоты.
7. Изучите свойства преобразования Фурье [Л.1, стр.35-38]. Ознакомьтесь с программой, приведенной в Приложении 6. Эта программа иллюстрирует (не доказывает) основные свойства преобразования Фурье. Выполните программу, сформулируйте соответствующее свойство, его доказательство и прокомментируйте результаты выполнения соответствующего фрагмента программы, относящееся к соответствующему свойству.
8. Составьте отчет по лабораторной работе. В отчете должны быть представлены
§ титульный лист,
§ название и цель работы,
§
формулировки (заголовки) пунктов
работы, команды и .m – файлы,
графики, комментарии, выводы.
9. Проверьте усвоение материала по контрольным вопросам, отчитайтесь в выполнении работы.
Литература
1. Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. пособие.- Новосибирск. Изд-во НГТУ, 1998 - ч.1.
2. Сергиенко А.Б. Цифровая обработка сигналов. СПб.: Питер, 2003.
3. Голышев Н.В., Щетинин Ю.И. Задачник-практикум по теории и обработке сигналов.: Учеб. пособие. Новосибирск: Изд-во НГТУ, 2001.
Web – ресурсы
1. http://tiger.cs.nstu.ru/tos/nperiodic/start.html
2. http://www.jhu.edu/~signals/ctftprops-mathml/index.htm
3. http://users.ece.gatech.edu/~bonnie/book/FourierTransformOfExponentialSignal/BIN/applet.html
Контрольные вопросы и упражнения
1. Запишите формулы прямого и обратного преобразования Фурье и объясните их физический смысл.
2. Как связаны преобразование Фурье и ряд Фурье? Получите и объясните соответствующее выражение.
3. Сформулируйте условия существования (сходимости) преобразования Фурье.
4. Что такое амплитудный спектр непериодического сигнала и каковы его особенности? Объясните физический смысл амплитудного спектра.
5. Как по спектральной плотности сигнала найти вклад определенной частоты в функцию сигнала?
6. Приведите определение фазового спектра сигнала. Что он выражает?
7. Как по спектру Фурье найти сам сигнал как временную функцию?
8.
Определите преобразование Фурье,
амплитудный и фазовый спектры сигнала ![]() .
Постройте графики спектров в Matlab. Используя свойство изменения масштаба, получите
преобразование Фурье функции
.
Постройте графики спектров в Matlab. Используя свойство изменения масштаба, получите
преобразование Фурье функции ![]() . Как
соотносятся сигналы
. Как
соотносятся сигналы ![]() и их спектры?
и их спектры?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.