НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов», 5 - й семестр
ЛАБОРАТОРНАЯ РАБОТА № 1
НЕПРЕРЫВНЫЕ И ДИСКРЕТНЫЕ
ПО ВРЕМЕНИ СИГНАЛЫ
Студент гр. АО-81
Васильева И.В.
Преподаватель
Доц. Щетинин Ю.И.
Новосибирск
2010
Цель работы:Знакомство со средой MATLAB, приобретение практических навыков генерирования непрерывных и дискретных по времени сигналов, построения графиков сигналов в среде MATLAB.
Ход работы:
1. Построение графика непрерывного по времени гармонического сигнала с помощью последовательности команд
A=10;
f=50;
phi=pi/5;
t=0:0.0005:0.04;
y=A*sin(2*pi*f*t-pi/5);
plot(t,y,'ro-')
grid
title('График гармоники')
xlabel('t, c')
ylabel('y(t)')
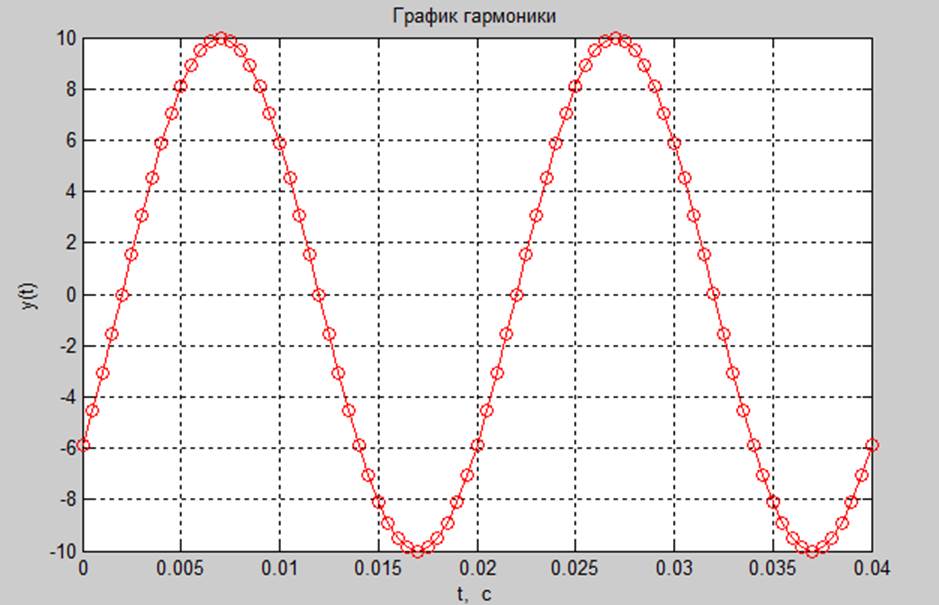
Рис.1. График непрерывного по времени гармонического сигнала с частотой 50 Гц, амплитудой 10 В, начальной фазой π/5, периодом 0,02 с.
P = (A^2)/2 =100/2=50 Вт - Мощность сигнала
В цифровой технике все сигналы дискретны. График непрерывной гармоники отличается от графика дискретной гармоники лишь тем, что в непрерывной гармонике точки соединены прямой линией (линейная интерполяция).
2. Построение графика дискретного по времени гармонического сигнала с помощью последовательности команд
>> A=10;
>> f=50;
>> phi=pi/5;
>> n=0:1:40; % Номер отсчета
>> Fs=1000; % Частота отсчетов
>> y=A*sin(2*pi*f*n/Fs-phi);
>> title('График дискретной гармоники')
>> figure
>> stem(n,y,'ro-')
>> grid
>> xlabel('n')
>> ylabel('y[n]')
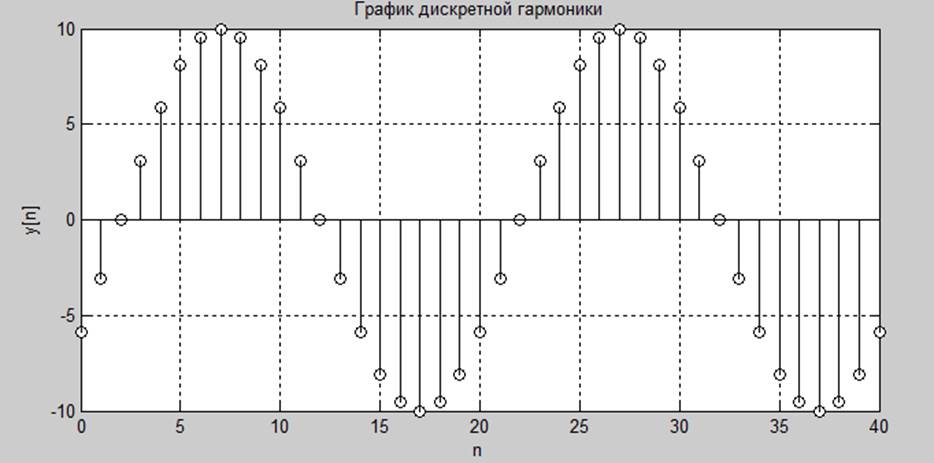
Рис. 2. Графика дискретного по времени гармонического сигнала с частотой 10 Гц, частотой отсчетов 100 Гц и начальной фазой π/2
3. Составление и выполнение последовательности команд для вычисления значений и построения графика нескольких (трех – пяти) периодов дискретной по времени гармоники с частотой 10 Гц, частотой отсчетов 100 Гц и начальной фазой π/2.
>> A=10;
>> f=10;
>> phi=pi/2;
>> n=0:1:40;
>> Fs=100;
>> y=A*sin(2*pi*f*n/Fs-phi);
>> figure
>> stem(n,y,'ro-')
>> grid
>> xlabel('n')
>> ylabel('y[n]')
>> title('График дискретной по времени гармоники')
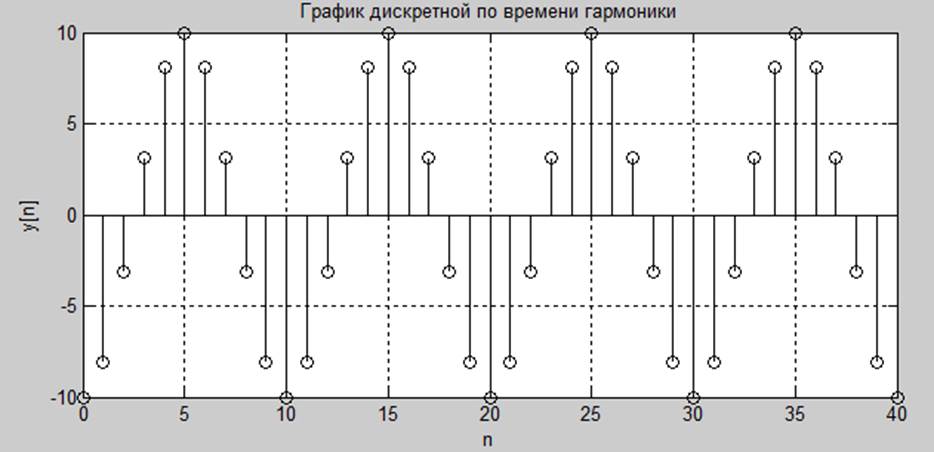
Рис.3. Графика дискретной по времени гармоники с частотой 10 Гц, частотой отсчетов 100 Гц и начальной фазой π/2.
5. Построение в одном графическом окне графиков
функций с помощью команды hold
а) ![]()
б) ![]()
в) ![]() .
.
x=0:0.1:15;
y1=sin(x);
hold on
y2=cos(x);
t=0:0.1:15;
xt=2*sin(t);
yt=cos(t);
grid
xlabel('x')
ylabel('y1(x),y2(x),y(x)')
plot(x,y1,x,y2,xt,yt)
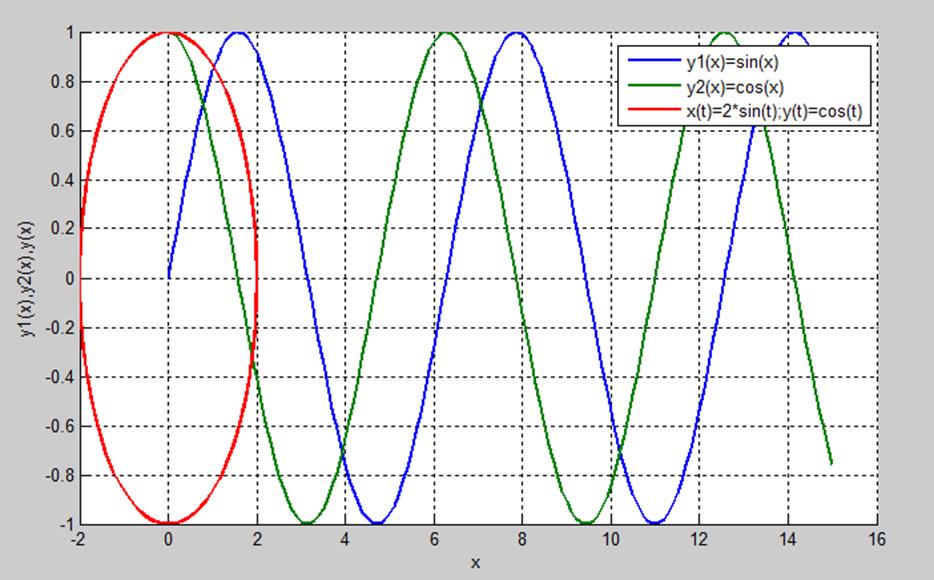
Рис.4. Графики функций
а)y1(x) = sin(x)
б) y2(x) = cos(x)
в) y(x), где x= 2sin(t), y=cos(t),
6. Вычисление вектора значений комплексной
экспоненты (гармоники) ![]() с показателем
затухания σ = - 0, 0693 и периодом Т = 2 секунды на интервале
с показателем
затухания σ = - 0, 0693 и периодом Т = 2 секунды на интервале ![]() .
.
6.1.Построение графика y с помощью команды plot(y).
>> t=0:10/500:10;
>> sigma = - 0.0693;
>> T = 2;
>> yt = exp((sigma+j*2*pi/T)*t);
>> plot (t,yt)
>> grid
>> xlabel ('x');
>> ylabel ('y(t)');
>> xlabel ('t');
>> title ('График функции вектора значений комплексной экспоненты (гармоники)')
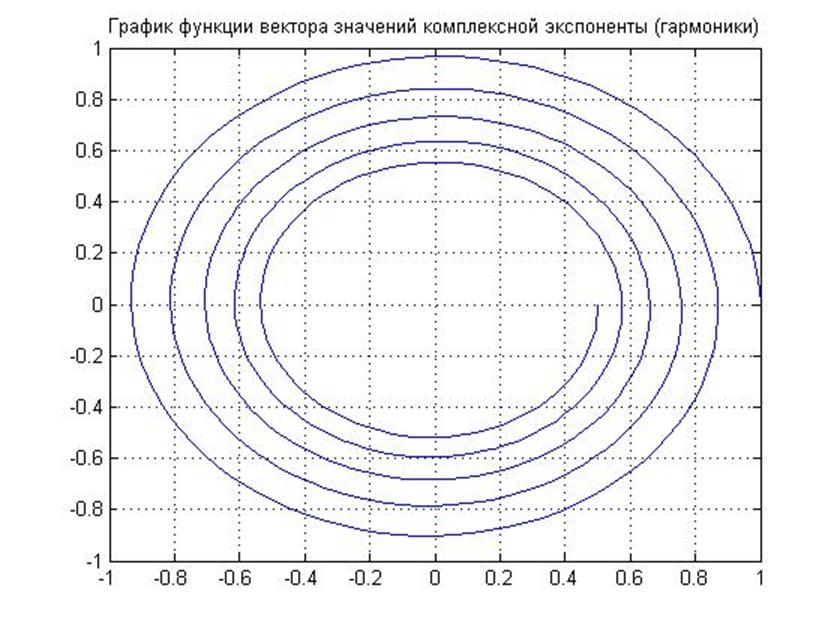
Рис.5. График функции ![]() с периодом Т = 2 секунды, с
показателем затухания σ = - 0, 0693
с периодом Т = 2 секунды, с
показателем затухания σ = - 0, 0693
6.2. Построение графиков действительной, мнимой части, модуля и аргумента y в зависимости от t.
t=0:10/500:10;
g=-0.0693;
T=2;
w=2*pi/T;
y=exp((g+j*w)*t);
subplot(4,1,1)
plot(t,real(y))
title('График действительной части y')
xlabel('t')
ylabel('y[t]')
subplot(4,1,2)
plot(t,imag(y))
title('График мнимой части y')
xlabel('t')
ylabel('y[t]')
subplot(4,1,3)
plot(t,abs(y))
title('График модуля y')
xlabel('t')
ylabel('y[t]')
subplot(4,1,4)
plot(t,angle(y))
title('График аргумента y')
xlabel('t')
ylabel('y[t]')
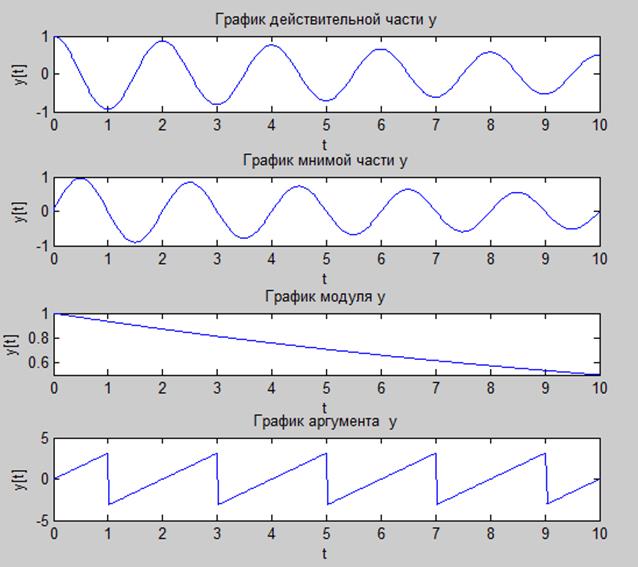
Рис.6. Графики действительной, мнимой части, модуля и аргумента y в зависимости от t.
Графики действительной и мнимой части имеют вид затухающий функции, график модуля имеет линийный вид, а график аргумента пилообразный периодический сигнал.
7. Построение в одном графическом окне графики сигналов прямоугольного импульса с длительностью шесть единиц и треугольного импульса с основанием четыре единицы.
osn1 = 6;
t = -10:0.001:10;
s1 = rectpuls (t-3, osn1);
s2 = rectpuls (t, osn1);
osn2 = 4;
s3 = tripuls (t-2, osn2);
subplot(3,1,1)
grid
plot (t,s1)
title(' Использование процедуры rectpuls для формирования прямоугольного импульса длительностью шесть единиц');
% титульная надпись
xlabel('t'); % осевая надпись по оси X
ylabel('s'); % осевая надпись по оси Y
axis ([-10,10,-1,2])
subplot(3,1,2)
grid
plot (t,s2)
title(' Использование процедуры rectpuls для формирования прямоугольного импульса длительностью шесть единиц');
% титульная надпись
xlabel('t'); % осевая надпись по оси X
ylabel('s'); % осевая надпись по оси Y
axis ([-10,10,-1,2])
subplot(3,1,3)
plot (t,s3)
grid
xlabel ('t')
ylabel ('s')
title(' Использование процедуры tripuls для получения треугольного импульса с основанием четыре единицы'); % титульная надпись
>>
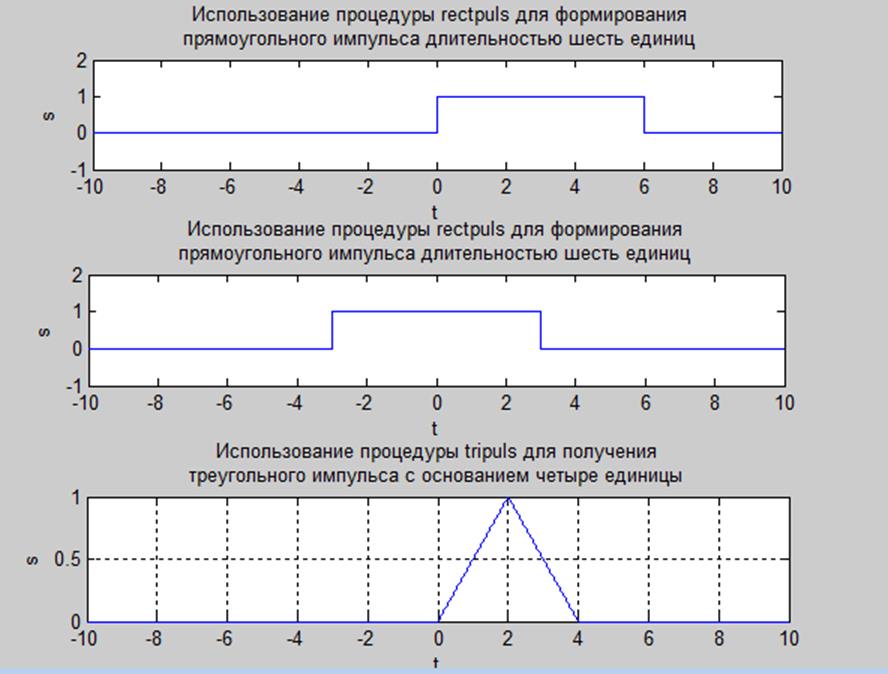
Рис.7.
Графики прямоугольных импульсов длительностью шесть единиц и ![]() - треугольных импульсов с основанием
четыре единицы
- треугольных импульсов с основанием
четыре единицы
8. Составление файл-функции и script – файлa для вычисления определенного интеграла с помощью метода прямоугольников
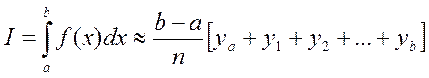 ,
,
8.1. Составление файл-функции для численного вычисления
интеграла от функции ![]() на интервале
на интервале ![]() , с использованием команды sum Matlab (без
использования цикла for).
, с использованием команды sum Matlab (без
использования цикла for).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.