НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 5
НЕПРЕРЫВНАЯ И ДИСКРЕТНАЯ СВЕРТКИ
Группа: АТ-23 Преподаватель:
Студенты: Рыбкина А. Щетинин Ю.И.
Кудрина Е.
Новосибирск, 2004
НЕПРЕРЫВНАЯ И ДИСКРЕТНАЯ СВЕРТКИ
Цель работы: Изучение понятия и свойств непрерывной и дискретной свертки, приобретение практических навыков вычисления свертки в среде Matlab.
1.
Свертка двух непрерывных по времени сигналов (непрерывная
свертка) определяется выражением
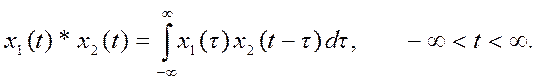
Численное вычисление непрерывной свертки может быть аппроксимировано конечной
суммой вида
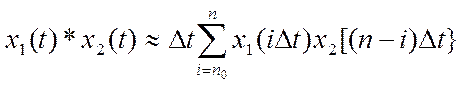 ,
,
где ![]() - интервал (шаг)
дискретизации.
- интервал (шаг)
дискретизации.
Файл-сценарий Matlab для приближенного вычисления
непрерывной свертки сигнала прямоугольной формы и экспоненциального сигнала:
% Численное вычисление непрерывной свертки
%
T=0.1; % шаг дискретизации
a=5;
i=0:50;
x1=exp(-a*i*T); % сигнал x1
x2=rectpuls(i-10,20); % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), plot(i*T,x1), title('x1')
subplot(412), plot(i*T,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), plot(k1*T,y),axis([0,4,0,0.4]),title('Свертка x1 и x2'),
% вычисление свертки с помощью функции conv()
subplot(414), plot(k1*T,T*conv(x1,x2))
title('Вычисление с помощью conv')
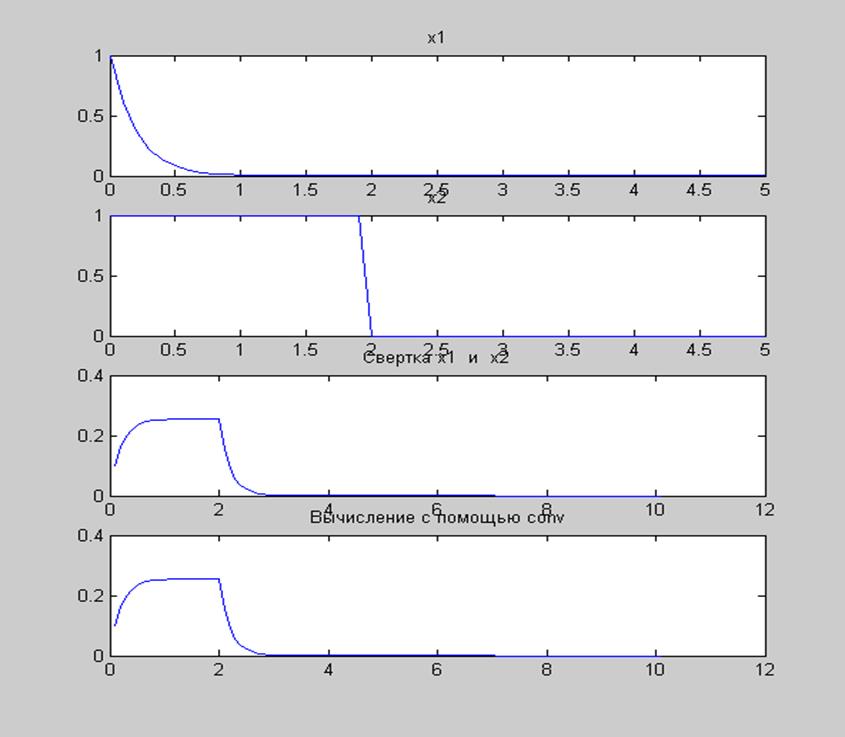
Рис.1 Графики сигналов x1=exp(-a*i*T) и x2=rectpuls(i-10,20) и их свертки,
полученной с помощью численного вычисления и функции conv.
Вывод: Из полученных графиков видно, что свертка, вычисленная численно и полученная с помощью функции conv одинакова.
2.
Вычисление
непрерывной сверткисигналов:![]()
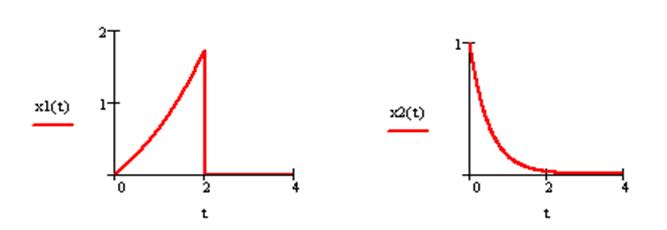
Файл-сценарий:
T=0.01; % шаг дискретизации
i=0:T:4;
t=0:T:2;
y=exp(0.5*t)-1; % сигнал x1
x1=[y zeros(1,200)];
x2=exp(-2*i); % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), plot(i,x1), title('x1')
subplot(412), plot(i,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), plot(k1,y),title('Свертка x1 и x2')
% вычисление свертки с помощью функции conv()
subplot(414), plot(k1,T*conv(x1,x2))
title('Вычисление с помощью conv')
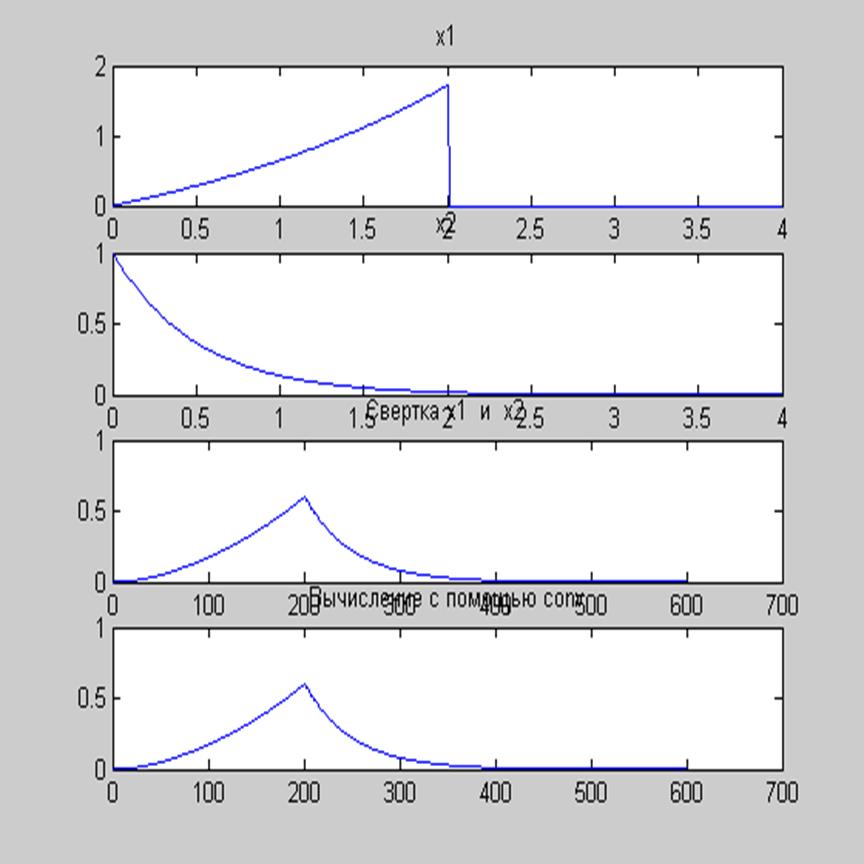
Рис.2 Графики сигналов x1=exp(0.5*t)-1, 0≤t≤2 и x2=exp(-2*i)
и их свертки.
Вывод: Получив свертку для сигналов x1 и x2 с помощью вычислений по соответствующей формуле, определили её также с помощью функции MatLab – conv и убедились, что результаты, полученные двумя способами, совпадают.
3.
Функция sqgen(L,T) с двумя параметрами L и T, которая генерирует прямоугольную последовательность импульсов (прямоугольную волну) длиной L отсчетов и периодом T отсчетов. Используется при этом функция square() Matlab.
function y=sqgen(L,T)
l=0:1:L-1;
f=1/T;
y1=square(2*pi*f*l);
y=y1;
4.
Создадим единичный импульс delta1=[1]. Вычислим свертку delta1 и sqgen(50, 10). Построим с помощью stem() графики сигналов и результата свертки.
Файл-сценарий:
T=1; % шаг дискретизации
i=0:1:49;
x1=1; % сигнал x1
x2=sqgen(50,10); % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), stem(0,x1), title('x1')
subplot(412), stem(i*T,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), stem(k1*T,y),title('Свертка x1 и x2'),
% вычисление свертки с помощью функции conv()
subplot(414), stem(k1*T,T*conv(x1,x2))
title('Вычисление с помощью conv')
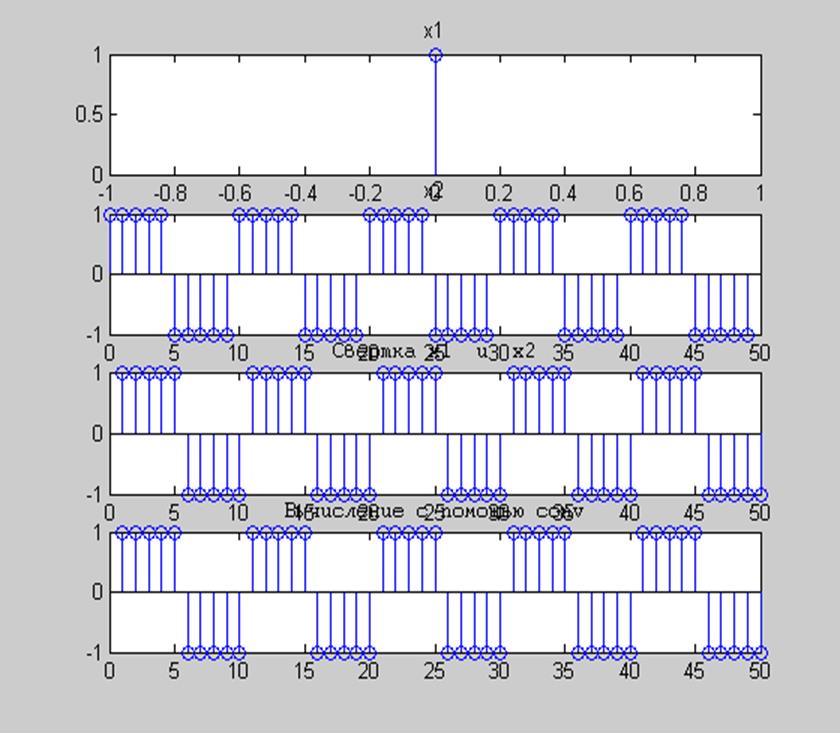
Рис.3 Сигналы x1=1 и x2=sqgen(50,10) и их свертка.
5.
Создадим с помощью команды delta2=[1 zeros(1,9)] другой импульс и вычислим свертку delta2 и sqgen(50, 10). Построим графики.
Файл-сценарий:
T=1; % шаг дискретизации
i=0:1:49;
y=1;
x1=[y zeros(1,9)]; % сигнал x1
x2=sqgen(50,10); % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), stem(x1), title('x1')
subplot(412), stem(i*T,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), stem(k1*T,y),title('Свертка x1 и x2'),
% вычисление свертки с помощью функции conv()
subplot(414), stem(k1*T,T*conv(x1,x2))
title('Вычисление с помощью conv')
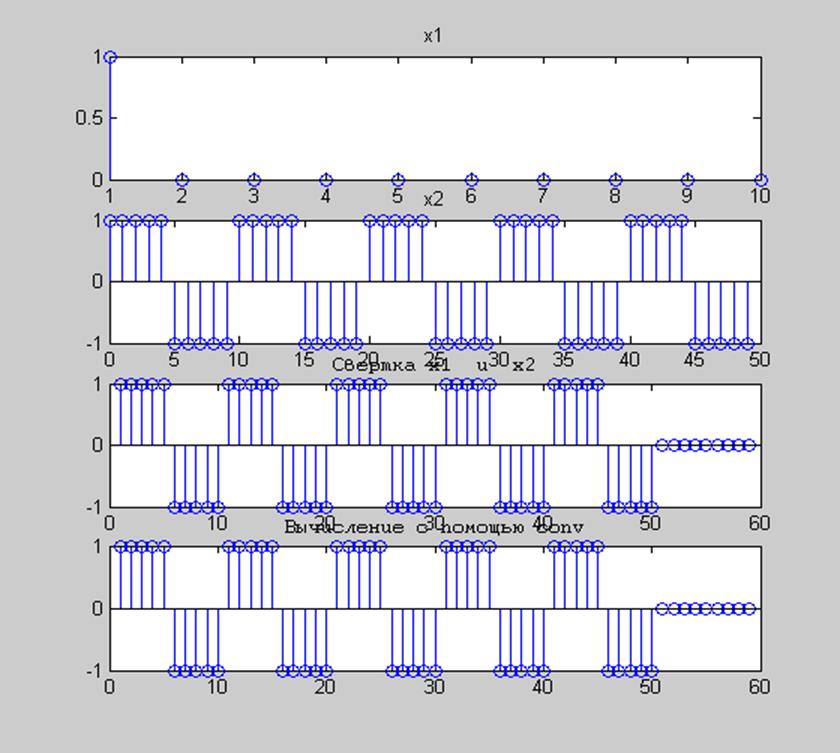
Рис.4 Графики сигналов x1=[y zeros(1,9)] и x2=sqgen(50,10) и их свертки.
Вывод: Сравнивая рисунки 3 и 4, видим, что с увеличением длительности одного из сигналов длина свертки также увеличивается, так как равна n1+n2-1, где n1 и n2- длина первого и второго сигналов соответственно.
6.
а) Создадим плоский импульс с помощью команды h1=[ones(1,2)]. Вычислим свертку h1 и sqgen(50, 10). Построим графики сигналов и свертки. б) Увеличим длину импульса до 8, снова вычислим свертку и построим её график.
а)
Файл-сценарий:
T=1; % шаг дискретизации
i=0:49;
x1=[ones(1,2)]; % сигнал x1
x2=sqgen(50,10); % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(311), stem(x1), title('x1')
subplot(312), stem(i*T,x2), title('x2')
% вычисление свертки с помощью функции conv()
k1=1:n1+n2-1;
subplot(313), stem(k1*T,T*conv(x1,x2))
title('Вычисление с помощью conv')
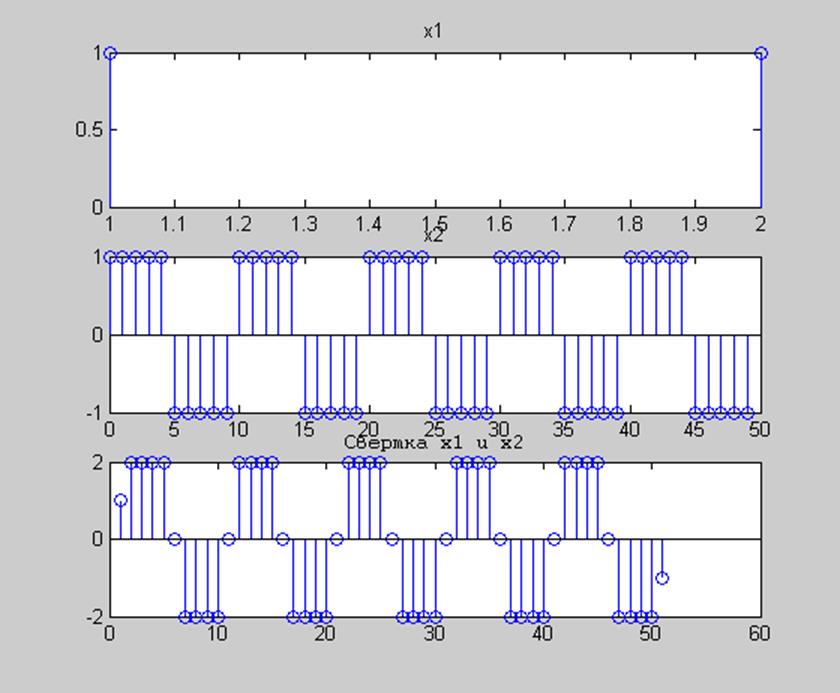
Рис.5 Графики сигналов x1=[ones(1,2)] и x2=sqgen(50,10) и их свертка.
б)
T=1;
i=0:49;
x1= [ones(1,8)];
x2=sqgen(50,10);
n1=length(x1);
n2=length(x2);
figure(2);
subplot(311);
stem(x1);
title('x1');
subplot(312);
stem(i*T,x2);
title('x2');
subplot(313);
k1=1:n1+n2-1;
stem(k1*T,T*conv(x1,x2));
title('Свертка x1 и x2');
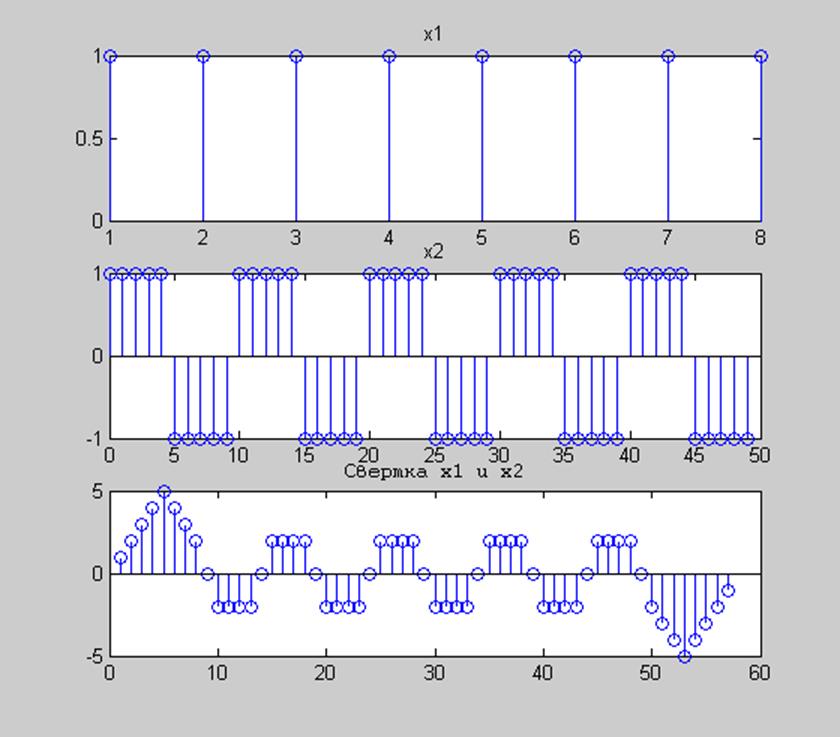
Рис.6 Графики сигналов x1=[ones(1,8)] и x2=sqgen(50,10) и их свертка.
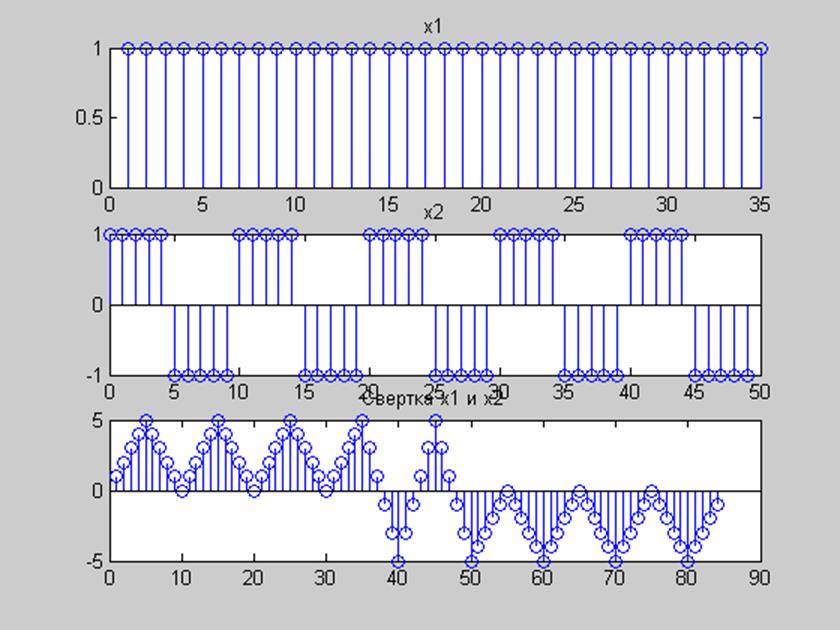
Вывод: Из рисунков 5 и 6 мы видим, что с увеличением длины сигнала x1 происходят существенные изменения свертки: чем больше единиц, тем сильнее искажается сигнал, так для 35 единиц получим следующий результат.
7.
Вычислим свертку сигналов
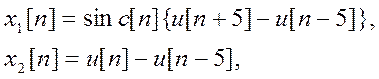
где 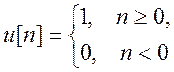 -
дискретная единичная ступенчатая функция.
-
дискретная единичная ступенчатая функция.
Построим графики сигналов и их свертки.
С помощью функции deconv() восстановим
сигнал ![]() из свертки, построим график результата.
из свертки, построим график результата.
Скрипт-файл:
n = input('Введите число отсчетов n = ');
u=[ones(1,n+5)];
for k=1:1:n
if k <= 5
x1(k)=sinc(k);
x2(k)=u(k);
else
x1(k)=sinc(k)*(u(k+5)-u(k-5));
x2(k)=u(k)-u(k-5);
end
end
y=conv(x1,x2);
t1=0:length(x1)-1; t2=0:length(x2)-1; t3=0:length(y)-1;
subplot(3,1,1), stem(t1,x1); title('x1');
subplot(3,1,2), stem(t2,x2); title('x2');
subplot(3,1,3), stem(t3,y); title('Свертка x1 и x2');
figure(2);
z=deconv(y,x2);
stem(t1,z);
Результат:
Введите число отсчетов n = 15
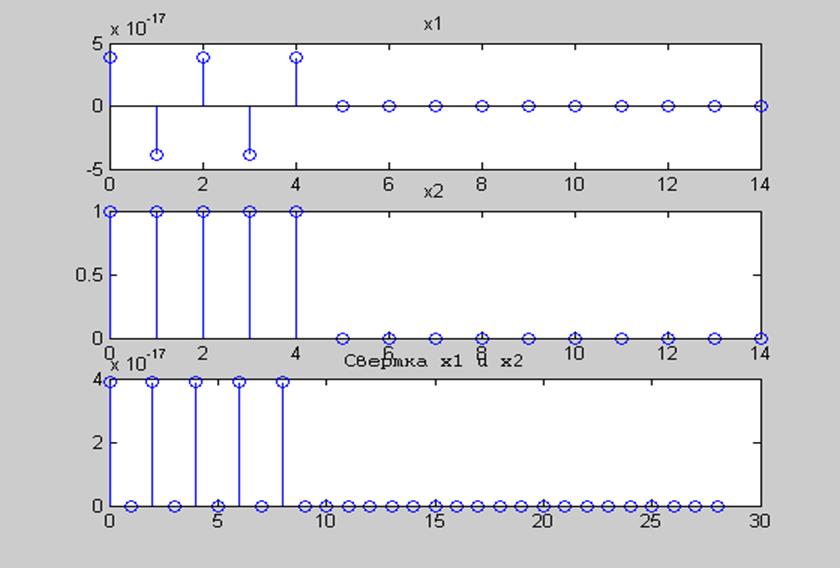
Рис.7 Графики сигналов x1(k)=sinc(k)*(u(k+5)-u(k-5)) и x2(k)=u(k)-u(k-5)
и их свертка.
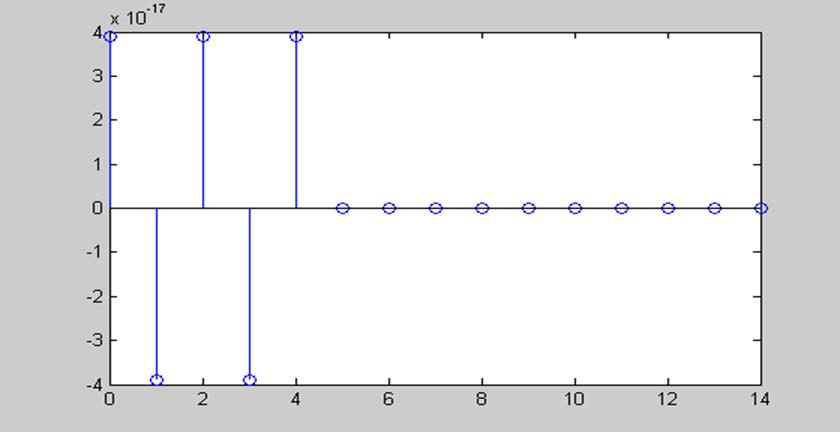
Рис.8 График сигнала x1(k)=sinc(k)*(u(k+5)-u(k-5)), восстановленного
из свертки с помощью функции deconv()
Вывод: Из данного примера видно, что с помощью функции deconv() можно восстановить из свертки исходный сигнал.
8.
Сгенерируем экспоненциальный дискретный сигнал длительностью 100 отсчетов и прямоугольный сигнал из 40 отсчетов. Выполним дискретную свертку этих сигналов (функция conv) и представим её график. Далее выполним свертку этих сигналов с помощью БПФ (круговая свертка). Для этого дополним каждый из сигналов до 256 отсчетов нулями, с помощью fft() получим ДПФ сигналов, перемножим преобразования Фурье и вычислим обратное (инверсное) ДПФ. Построим график модуля и сравним с результатами, полученными функцией conv().
t=0:1:99; % число отсчетов для экспоненциального сигнала
t1=0:39; % число отсчетов для прямоугольного сигнала
t2=0:1:138;
t3=0:1:255;
y1=exp(-t);
subplot(4,1,1); stem(t,y1);
title('Экспоненциальный дискретный сигнал')
y2=rectpuls(t1,80);
subplot(4,1,2); stem(t1,y2);
title('Прямоугольный сигнал')
y3=conv(y1,y2); % дискретная свертка сигналов
subplot(4,1,3); stem(t2,abs(y3));
title('Дискретная свертка сигналов');
y4=[y1 zeros(1,156)];
y5=[y2 zeros(1,216)];
y4p=fft(y4); y5p=fft(y5); % ДПФ сигналов
y6=y4p.*y5p;
y6p=ifft(y6); % Обратное ДПФ
subplot(4,1,4); stem(t3,abs(y6p));
title('Круговая свертка');
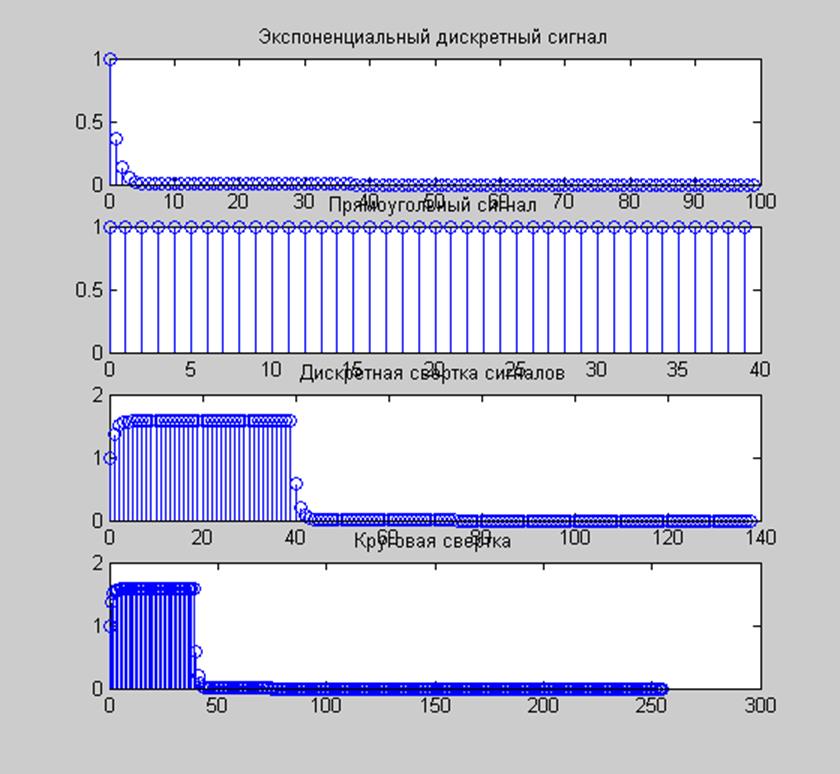
Рис.9 Графики сигналов y1=exp(t) и y2=rectpuls(t1,80) и их свертки, полученной
с помощью функции conv() и ДПФ
Вывод: Из полученных результатов видно, что графики модулей дискретной свертки сигналов, полученной с помощью функции conv, и круговой свертки, полученной с помощью ДПФ, одинаковы, но вычисление свертки вторым способом является более эффективным за счет использования быстрых алгоритмов вычисления ДПФ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.