НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов», 5 - й семестр
ЛАБОРАТОРНАЯ РАБОТА № 5
НЕПРЕРЫВНАЯ И ДИСКРЕТНАЯ СВЕРТКИ
Цель работы:Изучение понятия и свойств непрерывной и дискретной свертки, приобретение практических навыков вычисления свертки в среде Matlab.
Задание и порядок выполнения работы.
1. Ознакомьтесь с определениями и особенностями вычисления непрерывной и дискретной свертки по учебной литературе, например, [1] стр. 37-38, [2] стр. 7-8, 44-45.
2.
Свертка двух непрерывных по
времени сигналов (непрерывная свертка) определяется выражением
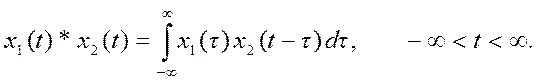
Численное вычисление непрерывной свертки может быть аппроксимировано конечной
суммой вида
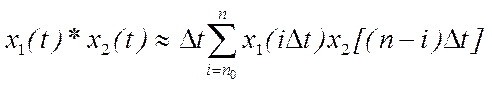 ,
,
где ![]() -
интервал (шаг) дискретизации.
-
интервал (шаг) дискретизации.
Свертка дискретных по времени сигналов (дискретная свертка) определяется
как
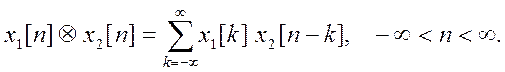
В Matlab
для вычисления дискретной свертки двух
последовательностей x и h служит
функция ![]() .
.
Ознакомьтесь с процедурой (файл-сценарий Matlab) для приближенного вычисления непрерывной свертки сигнала прямоугольной формы и экспоненциального сигнала, представленной в Приложении 1. Выполните процедуру и объясните её результаты на основе геометрического смысла операции свертки.
3. Используя файл-сценарий из Приложения 1 как прототип, напишите и выполните процедуру вычисления непрерывной свертки по индивидуальному заданию (Приложение 2). Объясните характер полученного результата на основе смысла операции свертки.
4. Напишите Matlab – функцию sqgen(L,T) с двумя параметрами L и T, которая генерирует прямоугольную последовательность импульсов (прямоугольную волну) длиной L отсчетов и периодом T отсчетов. Используйте при этом функцию square() Matlab.
5. Создайте единичный импульс delta1=[1]. Вычислите свертку delta1 и последовательности sqgen(50, 10). Постройте с помощью stem() графики сигналов и результата свертки. Объясните результат.
6. Создайте с помощью команды delta2=[1 zeros(1,9)] другой импульс и вычислите свертку delta2 и sqgen(50, 10). Постройте графики, объясните различия результатов п.5 и п.6.
7. Создайте плоский импульс с помощью команды h1=[ones(1,3)]. Вычислите свертку h1 и sqgen(50, 10). Постройте графики сигналов и свертки. Увеличьте длину импульса до 8, снова вычислите свертку и постройте её график. Объясните различия результатов. Что происходит со сверткой при увеличении длины импульса h1?
8. Ознакомьтесь с функцией deconv(x,h), выполняющей операцию, обратную операции свертки. Вычислите свертку сигналов
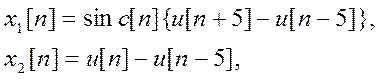
где 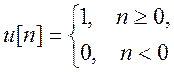 - дискретная единичная ступенчатая
функция.
- дискретная единичная ступенчатая
функция.
Постройте графики сигналов и
их свертки.
С помощью функции deconv() восстановите
сигнал ![]() из свертки, постройте график
результата. Для чего, в каких задачах целесообразно использовать обратную свертку?
из свертки, постройте график
результата. Для чего, в каких задачах целесообразно использовать обратную свертку?
Пояснения: а) в Matlab функция sinc(x) определена как 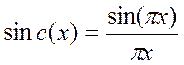 , поэтому для вычисления обычной sinc(x)=sin(x)/x в
Matlab аргумент следует поделить на π,
, поэтому для вычисления обычной sinc(x)=sin(x)/x в
Matlab аргумент следует поделить на π,
б) произведение вида ![]() в соответствии со смыслом функции u[n] означает вырезание из функции sinc(n)
последовательности длиной 11
отсчетов, симметричной относительно начала координат.
в соответствии со смыслом функции u[n] означает вырезание из функции sinc(n)
последовательности длиной 11
отсчетов, симметричной относительно начала координат.
9. Сгенерируйте экспоненциально убывающий дискретный сигнал длительностью 401 отсчетов с показателем затухания порядка 0,01 и прямоугольный дискретный сигнал из 200 отсчетов. Выполните дискретную свертку этих сигналов (используйте в качестве прототипа процедуру с циклом for из приложения 1) и определите при этом время выполнения свертки (функция cputime() Matlab). Представьте графики сигналов и их свертки.
Примечание: если функция cputime не
позволит определить время выполнения свертки, т.е. дает 0, то добавьте в
программе внешний цикл из 10 повторений вычисления свертки и разделите
полученное время вычисления на 10.
Далее выполните свертку этих сигналов в частотной области с помощью
БПФ (круговая свертка, см., например, Л[1], стр. 95- 98), определите время её
выполнения. Для вычисления свертки в частотной области дополните каждый из
сигналов до 1024 отсчетов нулями, с помощью fft() получите ДПФ сигналов, перемножьте их преобразования
Фурье и вычислите обратное (инверсное) ДПФ результата. При вычислении времени
вычисления учитывайте вышеприведенное примечание.
Постройте график модуля обратного ДПФ и сравните с ранее полученными результатами, прокомментируйте особенности и преимущества вычисления свертки с использованием ДПФ.
Пояснение: линейная (обычная) свертка сигналов длительностью М
и N отсчетов
требует приблизительно N*M операций
умножения и сложения, в то время как вычисление свертки в частотной области
(круговой свертки) с использованием БПФ требует примерно ![]() операций,
где L – размер
БПФ.
операций,
где L – размер
БПФ.
10. Сделайте необходимые пояснения, заключения и выводы, окончательно оформите отчет по лабораторной работе. В отчете должны быть представлены
§ титульный лист,
§ название и цель работы,
§
формулировки пунктов работы,
команды и .m – файлы,
графики,
комментарии, выводы.
ЛИТЕРАТУРА.
1. Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. пособие.- Новосибирск. Изд-во НГТУ, 1998 - ч.1, стр. 37-38.
2. Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. пособие. - Новосибирск. Изд-во НГТУ, 1998 - ч.2, стр. 7-3, 44-45.
3. Сергиенко А.Б. Цифровая обработка сигналов. - СПб.:
Питер, 2003,
стр. 211-213.
Web-ресурсы:
1. http//www.jhu.edu/~signals/convolve/index.html
2. http//www.jhu.edu/~signals/dicreteconv2/index.html
3. study/теория и обработка сигналов_2011/Tos_Demo/iconv
Контрольные вопросы и упражнения
1. Запишите и объясните выражение непрерывной свертки (интеграл наложения).
2. Поясните процедуру вычисления свертки на основе графического представления.
3. Используя геометрический смысл свертки, выполните свертку двух прямоугольных импульсов. Объясните результат.
4. Пусть выполняется свертка двух сигналов x1(t) и x2(t). Какой вид должен иметь x2(t), чтобы свертка точно воспроизводила сигнал x1(t)? Насколько это возможно для реальных систем?
5.
Вычислите аналитически свертку
сигналов ![]() , где u(t) – единичная ступенчатая функция.
, где u(t) – единичная ступенчатая функция.
6. Как можно вычислить непрерывную свертку численными методами?
7.
В среде Matlab
вычислите свертку сигналов
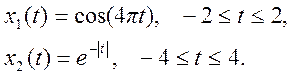
8. Сформулируйте и объясните свойство свертки преобразования Фурье.
9. Запишите выражение дискретной свертки и объясните механизм её вычисления.
10. Вычислите (без использования компьютера) дискретную
свертку двух последовательностей
x1 = {1 3
5 7}, x2 = {2
4 6}.
11. Вычислите аналитически свертку ![]() , где
, где 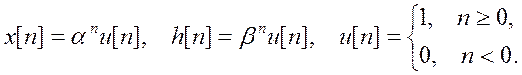
Изобразите график и характер результата для ![]() .
.
12. В среде Matlab вычислите дискретную свертку двух сигналов
![]() .
.
13. Объясните назначение и синтаксис функции deconv() Matlab. Примените эту функцию для восстановления сигнала x1[n] из предыдущего примера.
14. Поясните алгоритм и преимущества вычисления свертки в частотной области с помощью ДПФ.
15. Продемонстрируйте вычисление свертки с использованием
ДПФ для сигналов
![]() .
.
Приложение 1. Процедура вычисления непрерывной свертки
% Численное вычисление непрерывной свертки
T=0.1; % шаг дискретизации
a=5;
i=0:50;
x1=exp(-a*i*T); % сигнал x1
x2=rectpuls(i-10,20); % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), plot(i*T,x1), title('x1')
subplot(412), plot(i*T,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), plot(k1*T,y),title('Свертка x1 и x2')
% вычисление свертки с помощью функции conv()
subplot(414), plot(k1*T,T*conv(x1,x2))
title('Вычисление свертки с помощью conv')
Приложение 2. Индивидуальные задания
1. ![]()
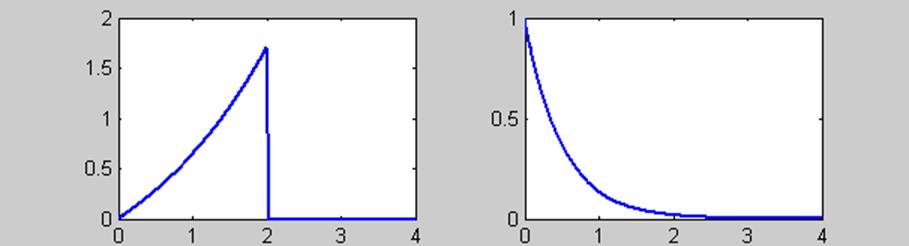
2.
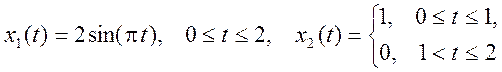
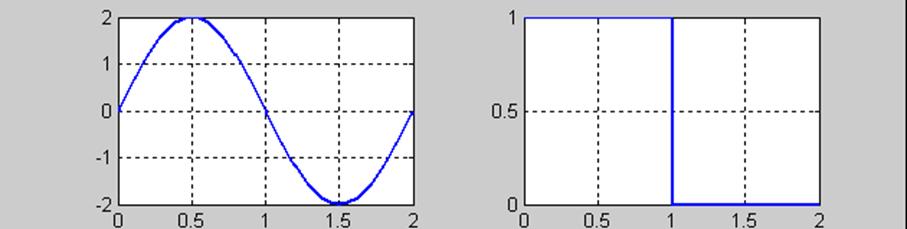
3. ![]()
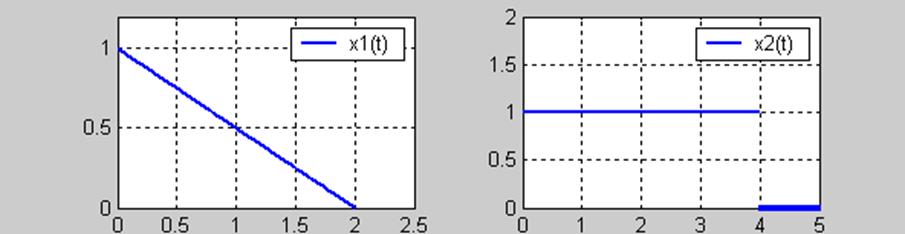
4. 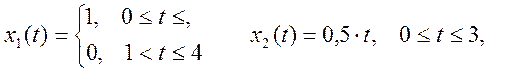
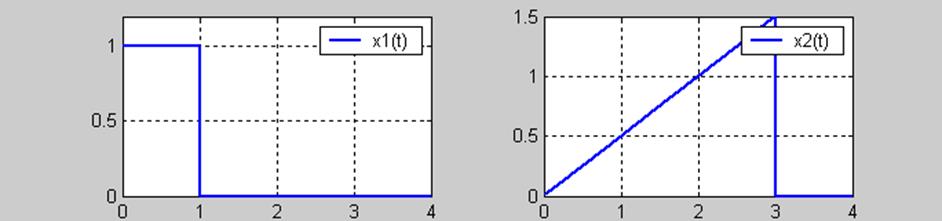
5.
![]()

6.
![]()
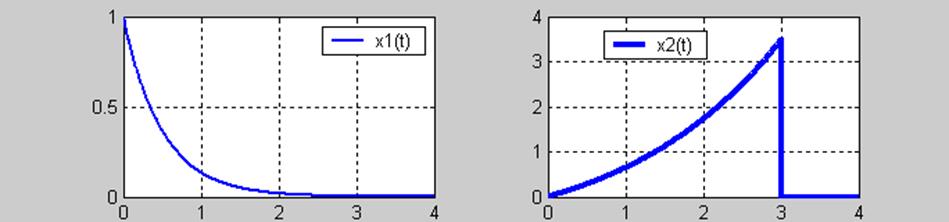
7. 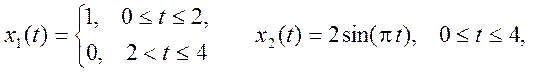
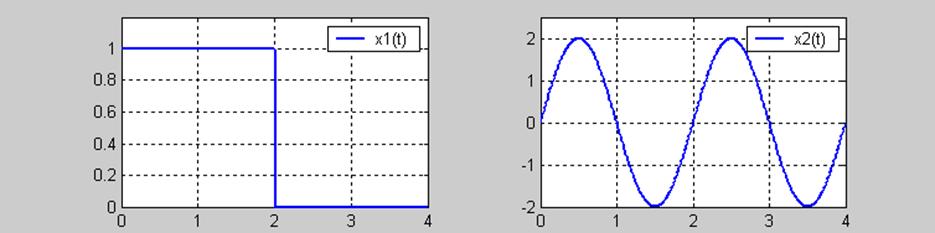
8. 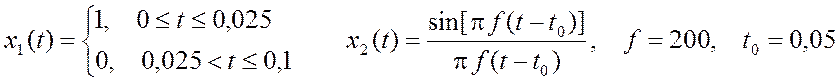
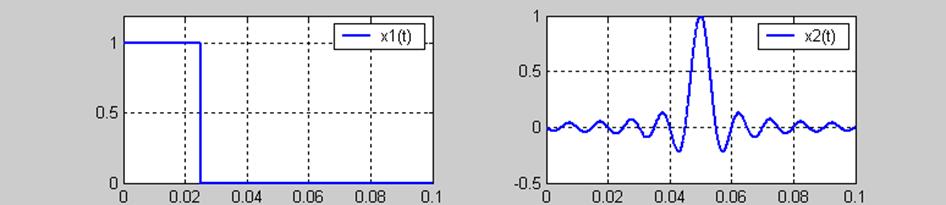
9.
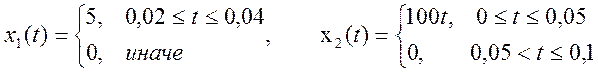
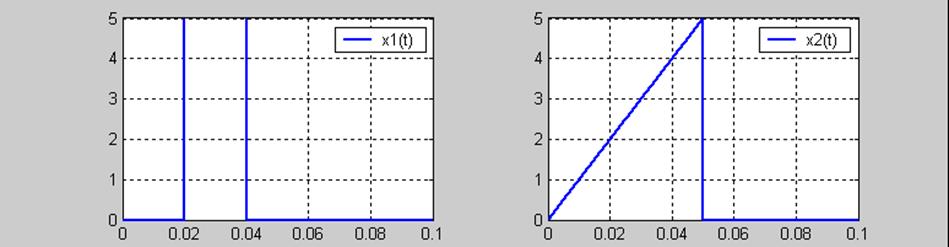
10.
![]()
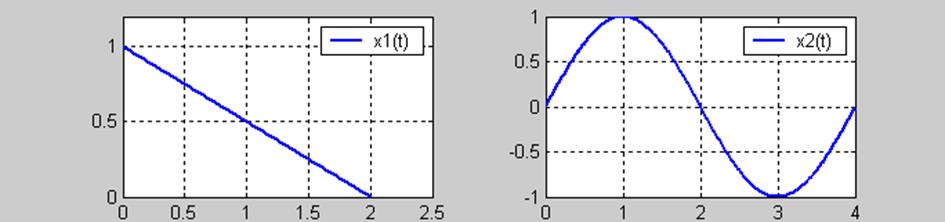
11.
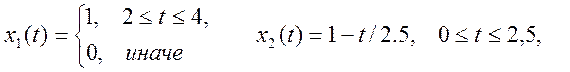
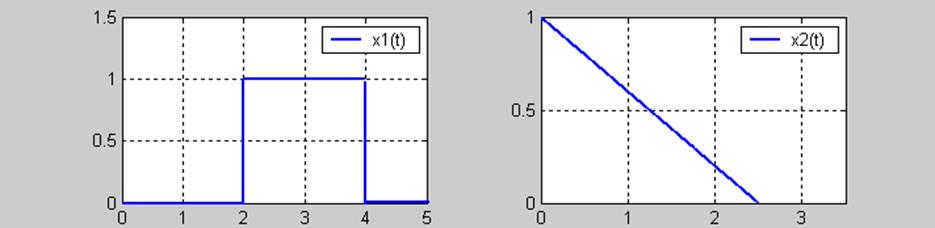
12.
![]()
Составил доц. Щетинин Ю.И.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.