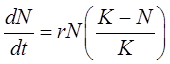 ,
(5)
,
(5)
где r – скорость роста численности популяции в отсутствие конкуренции; K – предельное значение численности популяции, при котором скорость роста становится равной нулю; t – номер популяции, N0 – начальная численность популяции.
Задание: найдите аналитическое решение задачи относительно параметра K. Сравните полученные результаты с результатами исследования имитационной модели.
3. Межвидовая конкуренция. В этом случае исследуется конкуренция популяций, потребляющих общий ресурс. Численность популяций описывается моделью Лотки–Вольтерра:
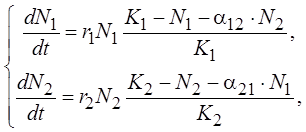 (6)
(6)
где N, r, K – параметры логистической модели (см. выше) для соответствующей популяции; α – параметр, отражающий интенсивности межвидовой конкуренции.
Задание: для заданных значений параметров модели исследуйте судьбу каждой из популяций: устойчивое сосуществование или полное вытеснение одной из них.
4. Система «хищник-жертва». В этой системе ситуация отличается от предыдущей тем, что «ресурс», за который идет борьба, – представители конкурирующей популяции. Численность популяций описывается системой уравнений:
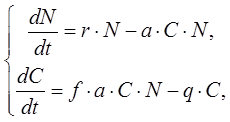 (7)
(7)
где С – численность популяции-хищника; N – численность популяции-жертвы; r – рост числа жертв в отсутствие хищников; q – снижение числа хищников в отсутствие жертв; a – коэффициент эффективности поиска хищниками жертв; f – коэффициент перехода пищи в потомство хищников.
Задание: исследовать судьбу каждой из популяций при заданных значениях параметров и характер колебательных процессов в системе в зависимости от соотношения начальных численностей популяций.
5. Гонка вооружений между двумя странами. Темпы прироста или уменьшения вооружений описываются следующей моделью:
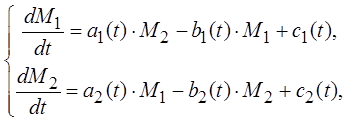 (8)
(8)
где a – скорость наращивания новых видов вооружений; b – скорость устаревания вооружений; с – уровень взаимной настороженности сторон.
Задание: для заданных функциональных зависимостей параметров а, b и c определите победителя в гонке вооружений.
6. Боевые действия между регулярными и партизанскими частями (модель Ланчестера):
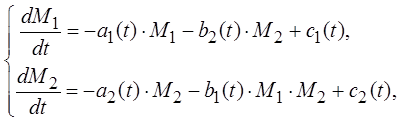 (9)
(9)
где M1 и M2 – численности регулярных и партизанских соединений соответственно; а – коэффициент потерь от небоевых причин; b – потери от действия противника; c – скорости поступления подкреплений.
Задание: для заданных значений параметров модели определите победителя конкурентной борьбы. Как влияет нелинейность данной системы уравнений на исход борьбы?
1. Антонов В.Ф. и др. Биофизика: Учебник для студентов вузов. – М.: ВЛАДОС, 1999. – 288 с.
2. Бочаров П.П., Печинкин А.В. Теория вероятностей. Математическая статистика. – М.: Гардарика, 1998. – 328 с.
3. Вентцель Е.С. Исследование операций. Задачи, принципы, методология: Учебное пособие для вузов. – М.: Дрофа, 2004. – 208 с.
4. Гультяев А. Визуальное моделирование в среде Matlab: учебный курс. – СПб: Питер, 2000. – 432 с.
5. ДьяконовВ. Simulink 4. Специальный справочник. – СПб: Питер, 2002. – 528 с.
6. Каган Б.М. Электронные вычислительные машины и системы: Учебное пособие для вузов. – М.: Энергоатомиздат, 1985. – 552 с.
7. Мамонова В.Г., Лыгина Н.И. Моделирование систем: метод. указ. к лабораторным работам. – Новосибирск: НГТУ, 2004. – 44 с.
8. Мирошник И.В. Теория автоматического управления. Линейные системы. – СПб.: Питер, 2005. – 336 с.
9. Могилев А.В., Пак Н.И., Хеннер Е.К. Практикум по информатике: Учеб. пособие для студентов вузов. – М.: Изд. центр. «Академия», 2002. – 608 с.
10. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. – М.: Физматлит, 2001. – 320 с.
содержание
Введение .......................................................................................... 3
Лабораторная работа № 1. Основные этапы разработки имитацион-
ной модели ................................................................................ 4
Лабораторная работа № 2. Стратегическое планирование модель-
ного эксперимента .................................................................. 11
Лабораторная работа № 3. Моделирование элементов цифровых
устройств ................................................................................ 13
Лабораторная работа № 4. метод статистических испытаний
Монте-Карло. Тактическое планирование модельного экспери-
мента ....................................................................................... 15
Лабораторная работа № 5. Моделирование системы массового
обслуживания методом Монте-Карло ..................................... 17
Лабораторная работа № 6. Моделирование кризисных ситуаций
в системах массового обслуживания...................................... 19
Лабораторная работа № 7. Моделирование системы автоматичес-
кого управления ..................................................................... 20
Лабораторная работа № 8. средства управления имитационной
моделью ................................................................................. 22
Лабораторная работа № 9. Моделирование параллельных процессов
с применением сетей Петри ................................................... 24
Лабораторная работа № 10. Исследование моделей соперничества 27
Список рекомендуемой литература ............................................... 30
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.