3. В системе присутствует некоторый информационный объект (файл). Доступ к объекту могут получать как писатели (изменяют содержимое объекта), так и читатели (не изменяют содержимое объекта). Одновременный доступ к объекту могут получить несколько читателей или только один писатель. читатели обладают бльшим приоритетом, чем писатели. При невозможности получения доступа в момент обращения пользователь попадает в одну из очередей – для читателей или писателей. Определите, чему должен равняться размер каждой из очередей, чтобы среднее время ожидания пользователями доступа к объекту не превышало заданного времени T. Моменты времени обращения пользователей к объекту – случайные величины с нормальным или пуассоновским законом распределения.
4. Преподаватель задает алфавит из некоторых символов и слово, составленное из символов данного алфавита. Требуется разработать сеть Петри, каждый переход которой обозначен одним из символов заданного алфавита. При запуске сети переходы инициализируются в таком порядке, чтобы составить заданное слово. Изменив начальную разметку сети, получите все возможные комбинации слов. Предложите способ генерации слов бесконечной и конечной длительности.
5. Рассматривается плоская область возбудимой мышечной ткани. В центре этой плоскости и перпендикулярно ей проходит кровеносный сосуд, стенки которого невозбудимы. Моделируется последовательность из N возбудимых клеток, расположенных по радиусу вокруг сосуда. С периодичностью T мс в одной из клеток этой последовательности возникает импульс возбуждения и начинает распространяться в обе стороны по волокну со скоростью V мс/клетку (клетки возбуждаются последовательно одна за другой, временем перехода в возбужденное состояние можно пренебречь). После возбуждения клетки на R мс переходят в состояние рефрактерности и становятся нечувствительными к повторному возбуждению. Одна из клеток последовательности испытывает нарушения обмена веществ и обладает скоростью проведения V0 и периодом рефрактерности R0, не равными соответствующим параметрам нормальных клеток. Исследуйте модель и определите, при каких численных значениях параметров пораженная клетка становится источником эктопического возбуждения.
6. Два корабля ведут между собой артиллерийский бой. Каждый из кораблей характеризуется тремя основными параметрами: количеством орудий N, скоростью движения M и интервалом времени T между последовательными N-орудийными залпами. Стрельба кораблей описывается двумя параллельными процессами. Залп с вероятностью P1 оказывается удачным, и все N снарядов попадают во вражеский корабль. При этом с вероятностью P2 выводится из строя одно орудие, в противном случае корпусу корабля наносится повреждение, и скорость падает на N единиц. Два последовательных попадания вынуждают весь экипаж корабля заняться тушением пожара на борту судна, и корабль пропускает следующий свой залп по противнику. Проигравшим бой считается корабль, потерявший все орудия или снизивший скорость до нуля. Оцените, сколько необходимо времени для победы одного из кораблей при равных значениях N, M, Т, P1, P2. Какой из этих параметров наиболее важен для достижения победы?
1. При моделировании каких процессов используются сети Петри? В чем заключаются достоинства и недостатки этих сетей?
2. Перечислите основные элементы сетей Петри.
3. Каким образом в сети Петри синхронизировать два параллельных процесса?
4. Как организовать очередь в сети Петри?
5. Постройте дерево покрываемости для разработанной вами сети Петри.
6. Сформулируйте следующие поведенческие свойства сетей Петри: достижимость, ограниченность, активность, обратимость, покрываемость, устойчивость, синхронное расстояние.
ИССЛЕДОВАНИЕ МОДЕЛЕЙ СОПЕРНИЧЕСТВА
Ознакомление с универсальными моделями описания различных видов соперничества – двухвидовой борьбы в популяциях, гонки вооружения, боевых действий. Разработка и исследование имитационных моделей соперничающих процессов и систем.
1. В соответствии с полученным вариантом разработайте имитационную модель соперничества.
2. Постройте графики, иллюстрирующие динамику исследуемых популяций, а также их фазовые траектории.
3. Для заданных преподавателем параметров модели ответьте на поставленный в задаче вопрос.
1. Внутривидовая конкуренция в популяции с дискретным размножением. К таким популяциям относят некоторые виды растений, насекомых и т.п., поколения которых четко разнесены во времени и особи разных поколений не сосуществуют.
Численность N таких популяций в зависимости от номера популяции t характеризуется следующим выражением:
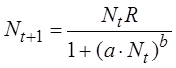 ,
(4)
,
(4)
где R – скорость воспроизводства в отсутствие конкуренции; N0 – начальная численность популяции; a – интенсивность внутривидовой конкуренции, b – характер установления численности популяции.
Задание: определите параметры системы, при которых характер установления численности популяции:
· монотонное установление стационарного значения численности;
· колебательный относительно некоторого стационарного значения;
· устойчивые предельные циклы изменения численности,
· случайные изменения численности без наличия явных закономерностей (динамический хаос).
2. Внутривидовая конкуренция в популяции с непрерывным размножением.
Характер изменения численности N популяции описывается так называемой логистической моделью:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.