2. Вычислите оценки следующих параметров системы: абсолютная пропускная способность (среднее число заявок, обслуживаемых в единицу времени); относительная пропускная способность (средняя доля пришедших заявок, обслуживаемых системой); вероятность отказа, среднее число занятых каналов. Используйте расчетный аналитический метод, основанный на уравнениях финальных вероятностей Колмогорова [3].
3. Получите оценки параметров системы, перечисленных в пункте 2, исследуя систему массового обслуживания методом статистических испытаний.
4. Сравните оценки, полученные в пунктах 2 и 3. Сделайте выводы.
5. Определите, в каких ситуациях работа данной системы будет невозможна из-за возникновения конфликтов.
1. Задача Эрланга. Система массового обслуживания с отказами (без очереди) и n каналами.
2. Одноканальная система массового обслуживания с неограниченной очередью.
3. Многоканальная система массового обслуживания с неограниченной очередью.
4. Одноканальная система массового обслуживания с ограниченной очередью.
5. Замкнутая система массового обслуживания с одним каналом обслуживания и m каналами заявок.
1. Какой поток случайных событий называется простейшим?
2. Перечислите основные типы систем массового обслуживания по числу каналов и наличию очереди, приведите примеры их практического применения.
3. Что такое схема гибели и размножения? Где она применяется?
4. При каких условиях поток Эрланга превращается из простейшего в регулярный?
МОДЕЛИРОВАНИЕ КРИЗИСНЫХ СИТУАЦИЙ
В СИСТЕМАХ МАССОВОГО ОБСЛУЖИВАНИЯ
Получение практических навыков использования метода статистических испытаний Монте-Карло при моделировании кризисных ситуаций в системах массового обслуживания.
1. Постройте имитационную модель для исследования работы пассажирского лифта в многоэтажном здании (N этажей). Все пассажиры едут с первого этажа и обслуживаются по очереди. Лифт вмещает одного человека. Время нахождения лифта в пути равняется N минутам, в зависимости от выбранного этажа. Используйте две случайные величины, распределенные равномерно: интервал между приходом людей к лифту (от 0 до Т минут) и время обслуживания (от 1 до N минут).
2. Постройте гистограммы времени нахождения в очереди и времени простоя лифта. Оцените средние значения этих величин.
3. Промоделируйте кризисную ситуацию, когда очередь к лифту неограниченно возрастает. При каких N и Т это происходит?
4. Повторите выполнение пунктов 2 и 3 для пуассоновского и нормального законов распределения случайных величин. Как влияет закон распределения на результаты моделирования?
5. Измените модель таким образом, чтобы время обслуживания складывалось из суммы N минут на поездку к нужному этажу и M минут на возвращение лифта на первый этаж после поездки предыдущего пассажира. Что изменилось?
6. Измените модель таким образом, чтобы она учитывала вероятность Р выхода лифта из строя при движении через каждый отдельный этаж. Какое среднее количество поездок приходится на один отказ лифта (при различных параметрах модели)?
7. Добавьте в модель второй пассажирский лифт. Люди идут к тому лифту, очередь к которому меньше. Сравните работоспособность этого варианта лифта с исходным. Снижает ли появление второго лифта вероятность возникновения кризисной ситуации? При каких параметрах модели?
8. Добавьте в модель возможность пассажирам подниматься не на лифте, а по лестнице. Пассажиры начинают пользоваться лестницей с вероятностью R, если длина очереди превышает S человек (очереди к лестнице не возникает). Снижает ли появление лестницы вероятность возникновения кризисной ситуации? При каких параметрах модели?
9. Сделайте выводы по работе.
МОДЕЛИРОВАНИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Построение имитационной модели системы автоматического управления – ПИД-регулятора. Исследование параметров системы.
1.
Разработать
имитационную модель пропорционально-инте-
грально-дифференциального регулятора выхода. В качестве объекта управления используется
непрерывная система следующего вида:
![]() ,
(1)
,
(1)
где y(t) – выходная (регулируемая) переменная; W0(p) – передаточная функция системы; u(t) – входное (управляющее) воздействие; f(t) – возмущающее воздействие.
Передаточная функция, в свою очередь, определена таким образом:
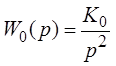 ,
(2)
,
(2)
где K0 – некоторый коэффициент.
ПИД-регулятор описывается выражением
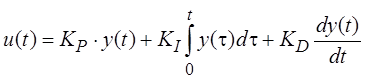 , (3)
, (3)
где KP, KI, KD – некоторые коэффициенты.
Значения постоянных коэффициентов, характер возмущающего воздействия и начальные установки регулятора и системы задаются преподавателем.
2. Осуществить моделирование имитационной модели при различных параметрах дискретизации и в различных режимах модельного времени. Сделать выводы.
3. Определить параметры переходных процессов в системе, используя метод статистических испытаний Монте-Карло.
4. Смоделировать ситуацию потери устойчивости системой.
1. Предложите способ определения передаточной функции рассматриваемой системы средствами Simulink.
2. Какими достоинствами и недостатками обладает ПИД-регулятор по сравнению с другими типами пропорциональных регуляторов?
3. Каким образом длительность интервала дискретизации влияет на точность работы регулятора?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.