Линейные непрерывные стационарные системы. Вариант 7

            МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

ЛАБОРАТОРНАЯ  РАБОТА  № 7

ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ

СТАЦИОНАРНЫЕ  СИСТЕМЫ

Вариант 7

Группа: АТ-73                                                                             Преподаватель:

Студент: Бердников П.А.                                                           доц. Щетинин Ю.И.

Новосибирск

 2009

Цель работы:  знакомство с динамическими характеристиками  линейных непрерывных стационарных (инвариантных во времени) систем  и их использованием для анализа систем в среде MATLAB.

1.  Определение передаточной функции активного фильтра.

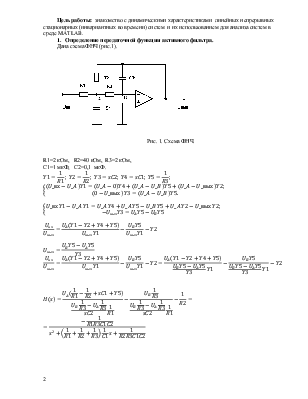
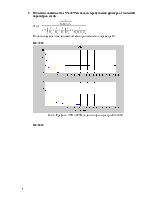
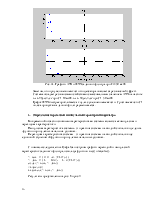
Дана схема ФНЧ (рис.1).

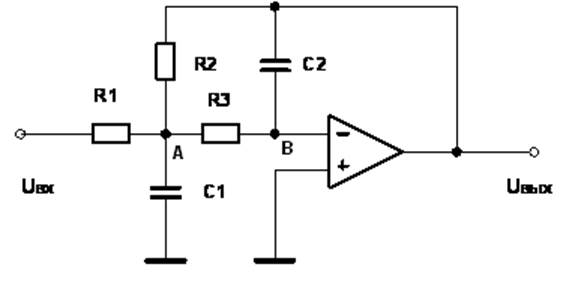
Рис. 1. Схема ФНЧ.

R1=2 кОм,   R2=40 кОм,  R3=2 кОм,
C1=1 мкФ,   C2=0,1  мкФ.

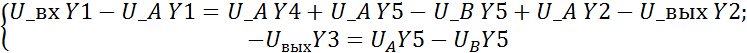
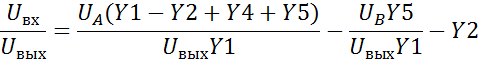
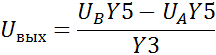
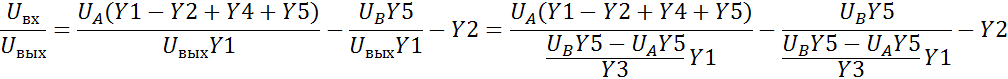
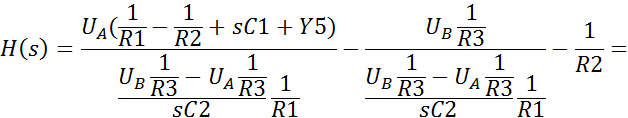
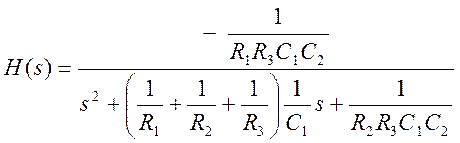
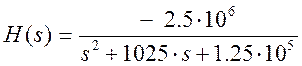
2.  Определение нулей и полюсов передаточной функции фильтра.

Корни многочлена  знаменателя передаточной функции называются полюсами системы.

Корни многочлена  числителя передаточной функции называются нулями системы.

С помощью следующего script-файла найдём полюса передаточной функции (9), коэффициент усиления K фильтра. Для этого будем использовать функции roots() и tf2zp().

Построим также диаграмму нулей и полюсов с помощью функции zplane().

% коэффициенты числителя

C_num = [0 0 -2.5*10^6];

zeros = roots(C_num)

% коэффициенты знаменателя

C_den = [1   1025   1.25*10^5];

poles = roots(C_den)

[Z,P,K] = tf2zp(C_num,C_den)

% диаграмма нулей и полюсов

zplane(Z, P)

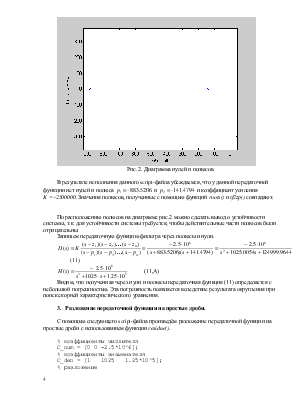
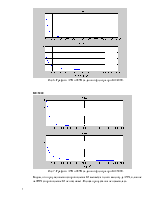
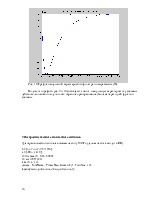
Диаграмма нулей и полюсов представлена на рис. 2.

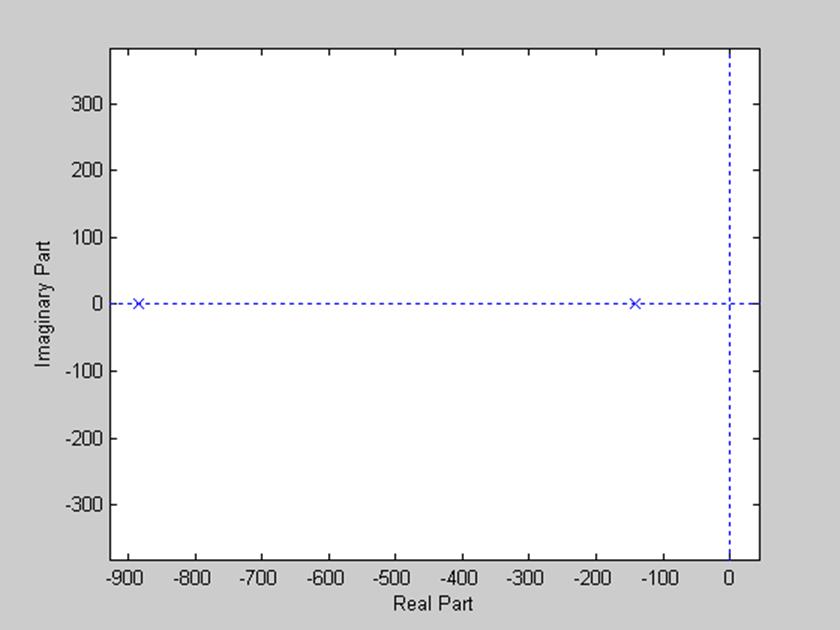
Рис. 2. Диаграмма нулей и полюсов.

В результате исполнения данного script-файла убеждаемся, что у данной передаточной функции нет нулей и полюса  и  и коэффициент усиления

K = -2500000. Значения полюсов, полученные с помощью функций roots() иtf2zp() совпадают.

По расположению полюсов на диаграмме рис.2 можно сделать вывод о устойчивости системы, т.к. для устойчивости системы требуется, чтобы действительные части полюсов были отрицательны.

Запишем передаточную функцию фильтра через полюсы и нули.

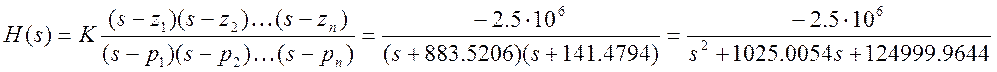                   (11)

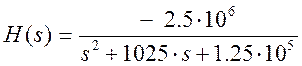           (11,А)

Видим, что полученная через нули и полюсы передаточная функция (11) определяется с небольшой погрешностью. Эта погрешность появляется вследствие результата округления при поиске корней характеристического уравнения.

3.  Разложение передаточной функции на простые дроби.

С помощью следующего script-файла произведём разложение передаточной функции на простые дроби с использованием функции residue().

% коэффициенты числителя

C_num = [0 0 -2.5*10^6];

% коэффициенты знаменателя

C_den = [1   1025   1.25*10^5];

% разложение

[R,P,K] = residue(C_num,C_den)

В результате исполнения данного script-файла получили

R =

  1.0e+003 *

    3.3691

   -3.3691

P =

 -883.5206

 -141.4794

K =

     -2.5*10^6

Используя выходные аргументы функции residue(), запишем разложение передаточной функции на простые дроби. 

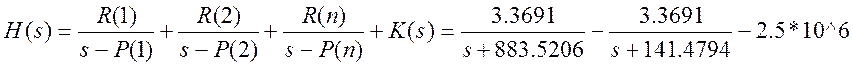                                           (12)

Упростим выражение (12) для сравнения с исходной передаточной функцией (10).

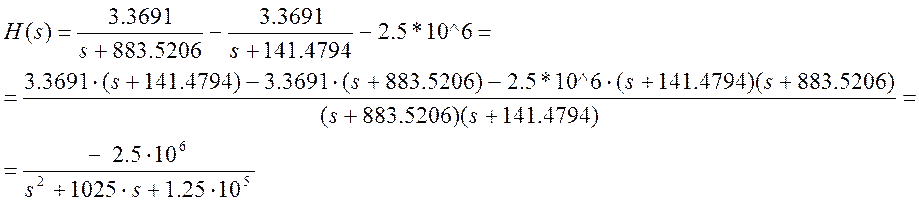      (13)

Видим, что выражение (13) совпадает с исходной передаточной функцией (10).

Данную систему можно представить как параллельно соединённые системы с передаточными функциями, равными слагаемым выражения (12).

4.  Построение графиков АЧХ и ФЧХ фильтра и диаграммы Боде.

В частотной области важнейшей характеристикой системы является её частотная характеристика, которую можно получить из передаточной функции системы заменой .

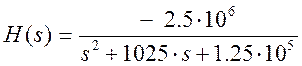                                                                                                      (14)

АЧХ характеризует изменение амплитуды гармоники при прохождении её через систему, а ФЧХ – изменение фазы гармоники.

С помощью следующего script-файла построим графики АЧХ и ФЧХ заданного фильтра, используя функцию freqs().

% коэффициенты числителя

C_num = [0 0 -2.5*10^6];

% коэффициенты знаменателя

C_den = [1   1025   1.25*10^5];

[h,w] = freqs(C_num,C_den);

subplot(2,1,1);

plot(w, abs(h));

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('АЧХ');

subplot(2,1,2);

plot(w, angle(h));

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('ФЧХ');

xlabel('Частота, рад/с');

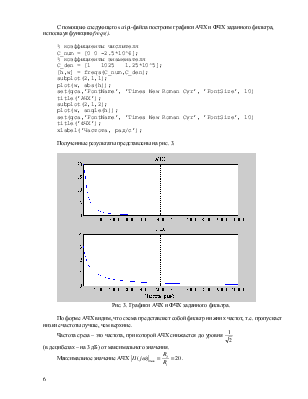
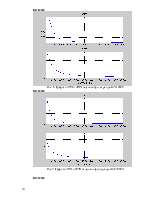
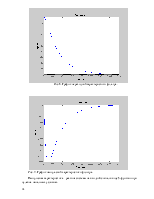
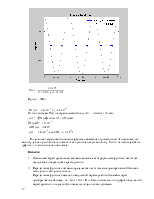
Полученные результаты представлены на рис. 3.

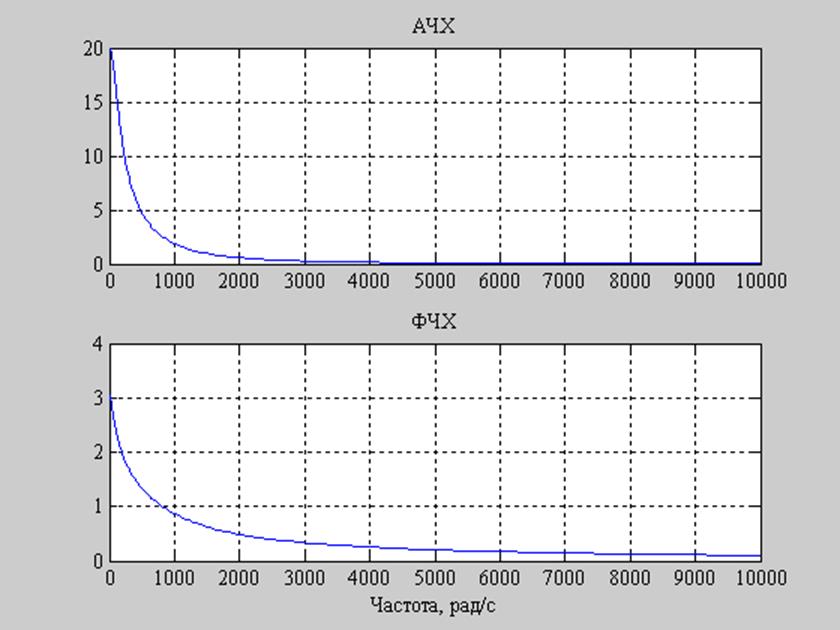
Рис. 3. Графики АЧХ и ФЧХ заданного фильтра.

По форме АЧХ видим, что схема представляет собой фильтр нижних частот, т.е. пропускает низкие частоты лучше, чем верхние.

Частота среза – это частота, при которой АЧХ снижается  до уровня

(в децибелах – на 3 дБ) от максимального значения.

Максимальное значение АЧХ .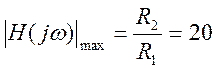

АЧХ снижается в  раз от на частоте среза  или .

С помощью следующего script-файла построим диаграмму Боде для заданного фильтра, используя функцию bode().

% коэффициенты числителя

C_num = [0 0 -2.5*10^6];

% коэффициенты знаменателя

C_den = [1   1025   1.25*10^5];

bode(C_num,C_den);

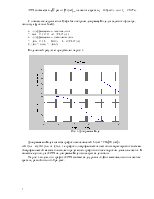
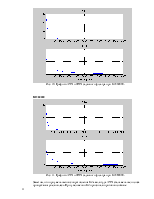
Полученный результат представлен на рис. 4.

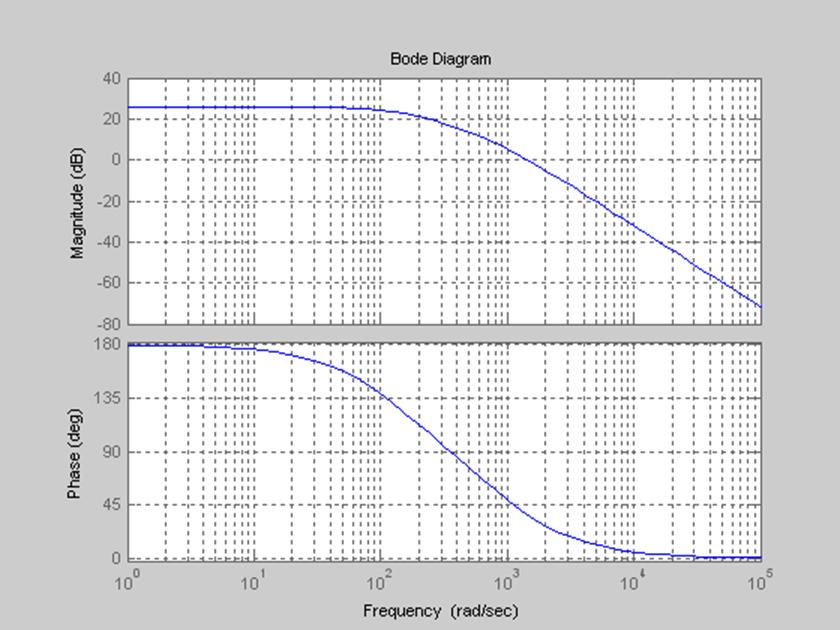
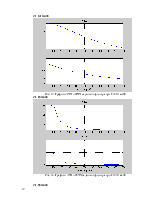
Рис. 4. Диаграмма Боде.

Диаграммами Боде являются графики зависимостей  и  от , т.е. графики логарифмических частотных характеристик системы. Логарифмический масштаб позволяет представлять графики в более широком диапазоне частот. В качестве единиц для ЛАЧХ на диаграмме Боде используются децибелы.

На рис. 4 видим, что  график ЛАЧХ снижается до уровня -3 дБ от максимального на частоте среза  равной около 130 рад/сек.