5. Изучение
зависимости АЧХ, ФЧХ и полосы пропускания фильтра от значений параметров схемы.
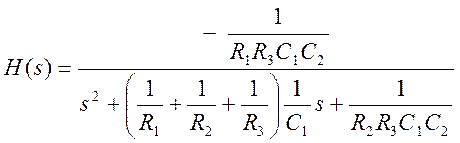
Понаблюдаем за поведением системы при изменении параметра R1.
R1=3000
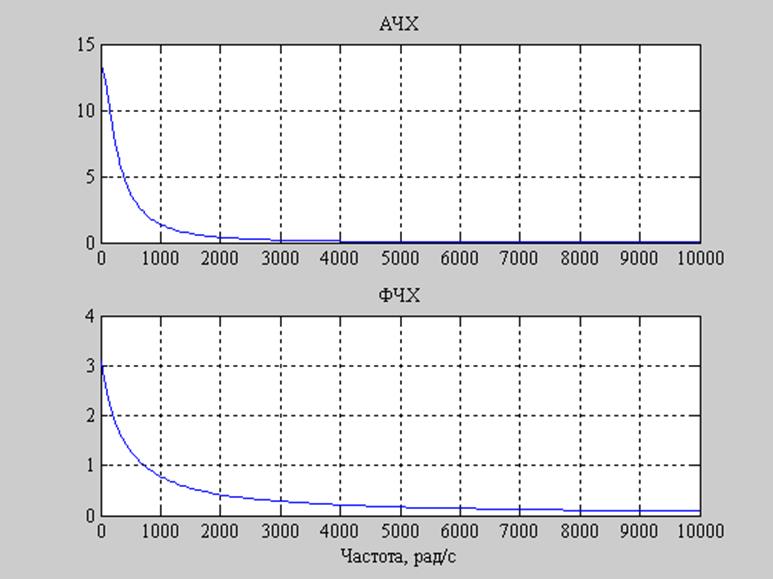
Рис. 5. Графики АЧХ и ФЧХ заданного фильтра при R1=3000.
R1=4000
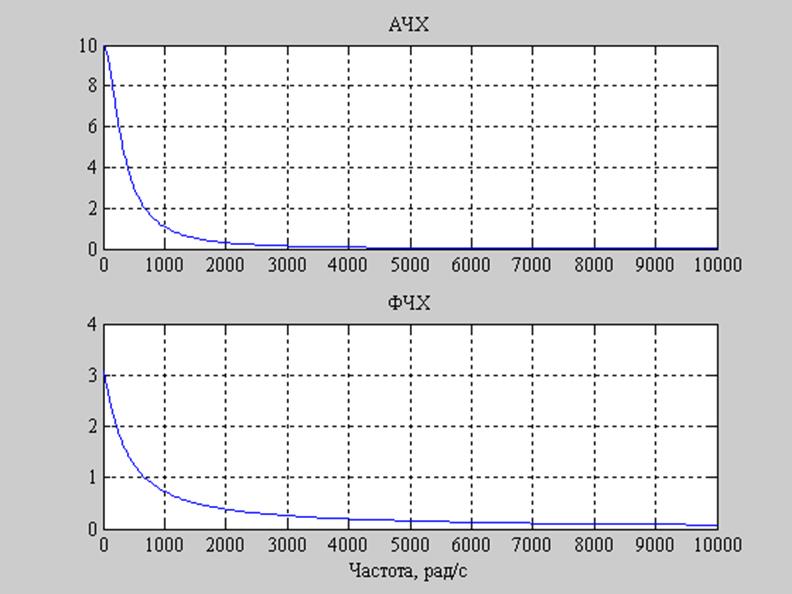
Рис. 6. Графики АЧХ и ФЧХ заданного фильтра при R1=4000.
R1=5000
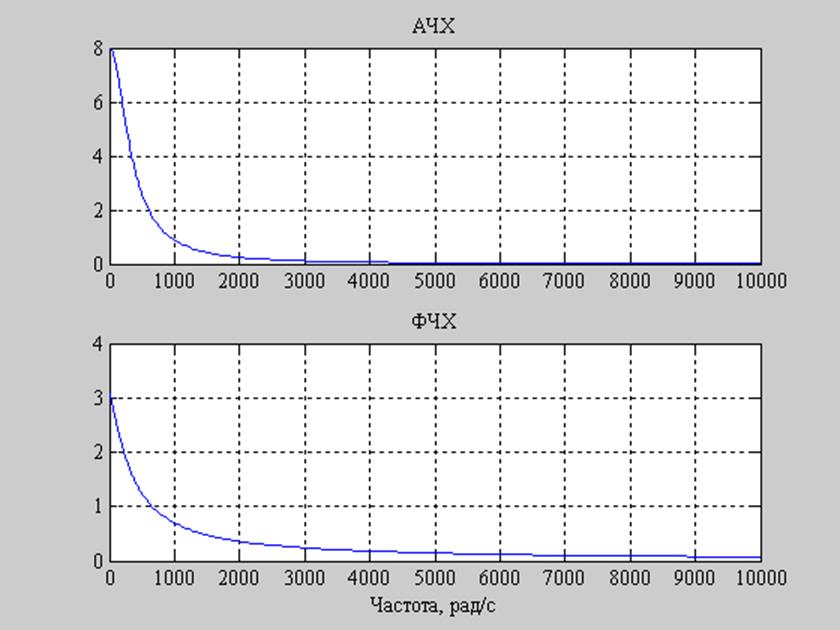
Рис. 7. Графики АЧХ и ФЧХ заданного фильтра при R1=5000.
Видим, что при увеличении сопротивления R1 меняется только амплитуда АЧХ, влияние на ФЧХ сопротивление R1 не оказывает. Полоса пропускания не изменилась.
R2=10000
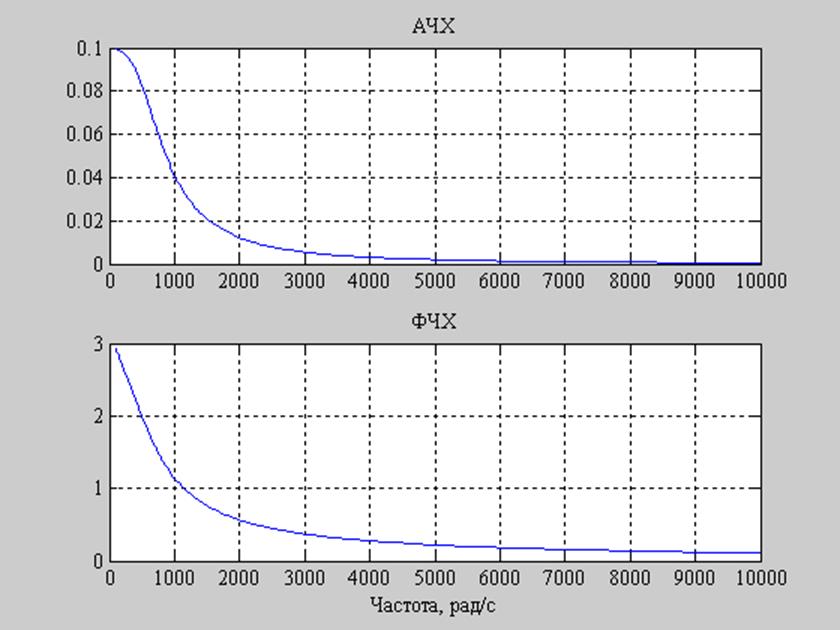
Рис. 8. Графики АЧХ и ФЧХ заданного фильтра при R2=10000.
R2=20000
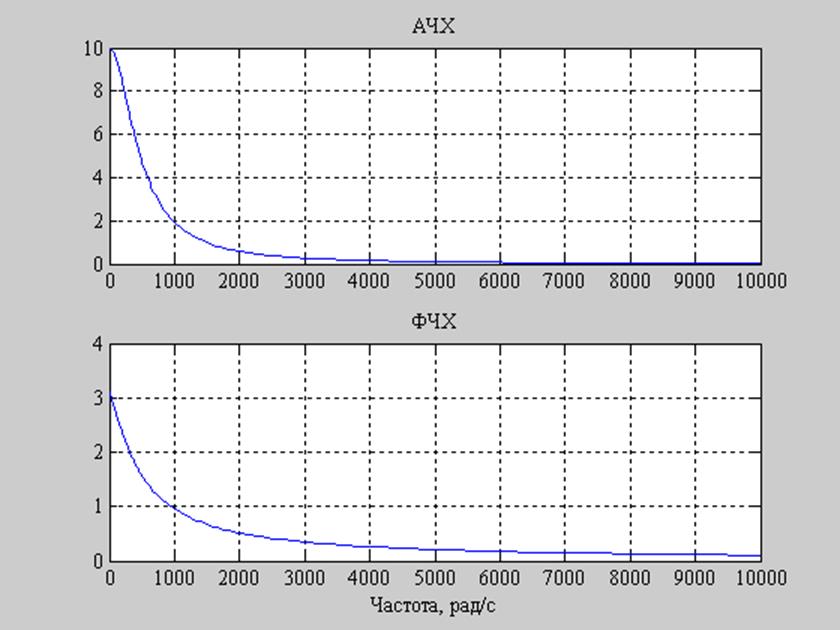
Рис. 9. Графики АЧХ и ФЧХ заданного фильтра при R2=20000..
R2=60000
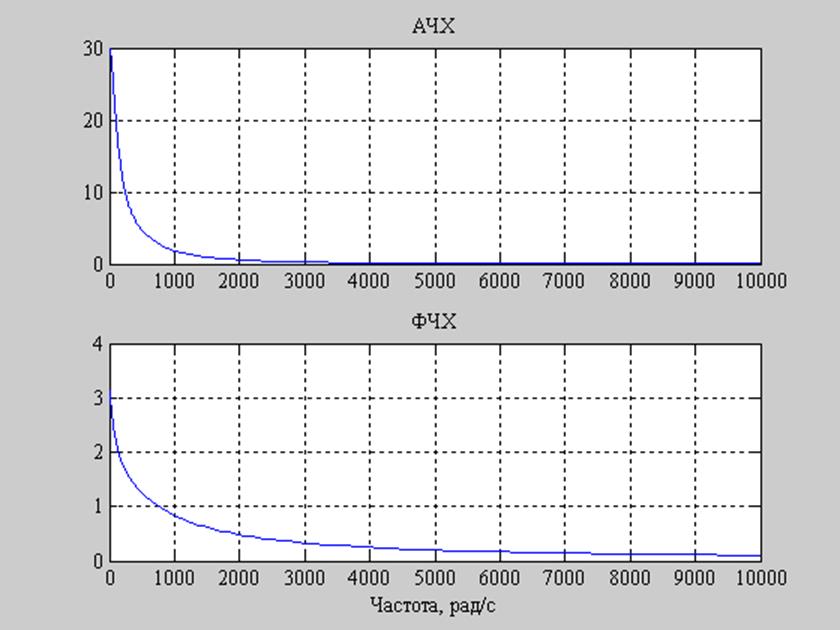
Рис. 10. Графики АЧХ и ФЧХ заданного фильтра при R2=60000..
R2=80000
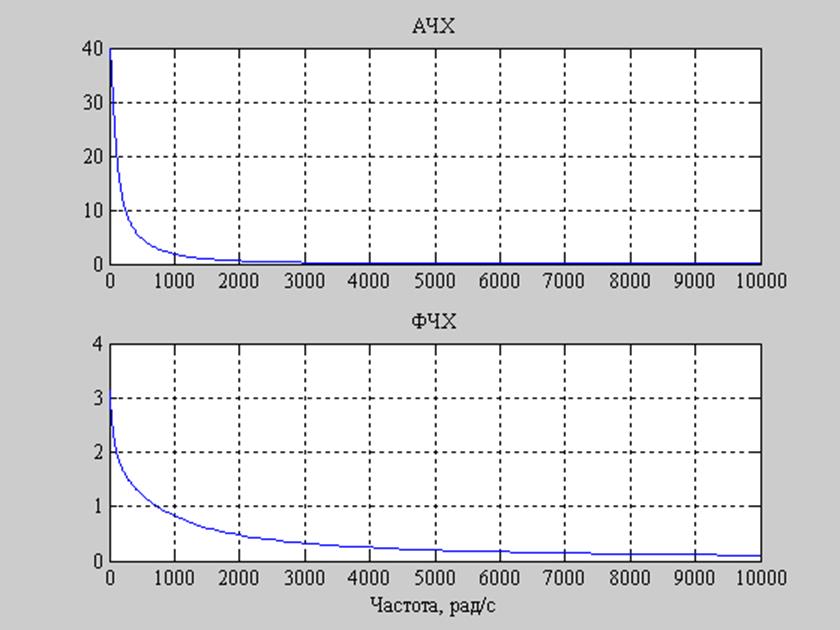
Рис. 11. Графики АЧХ и ФЧХ заданного фильтра при R2=80000..
Заметим, что при уменьшении сопротивления R2 амплитуда АЧХ стала меньше, полоса пропускания увеличилась. При увеличении R2 произошло противоположное.
С1=0.1 мкФ
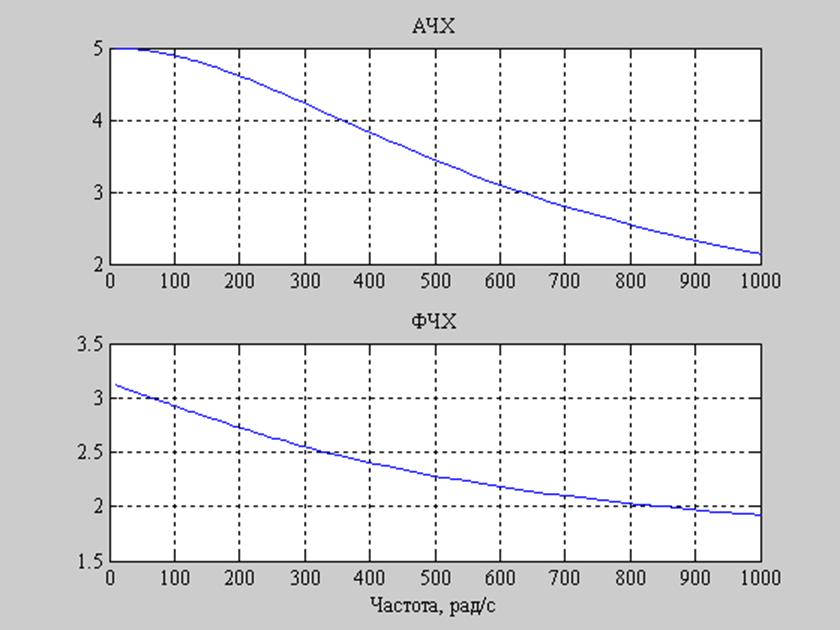
Рис. 12. Графики АЧХ и ФЧХ заданного фильтра при C1=0.1 мкФ.
С1=10 мкФ
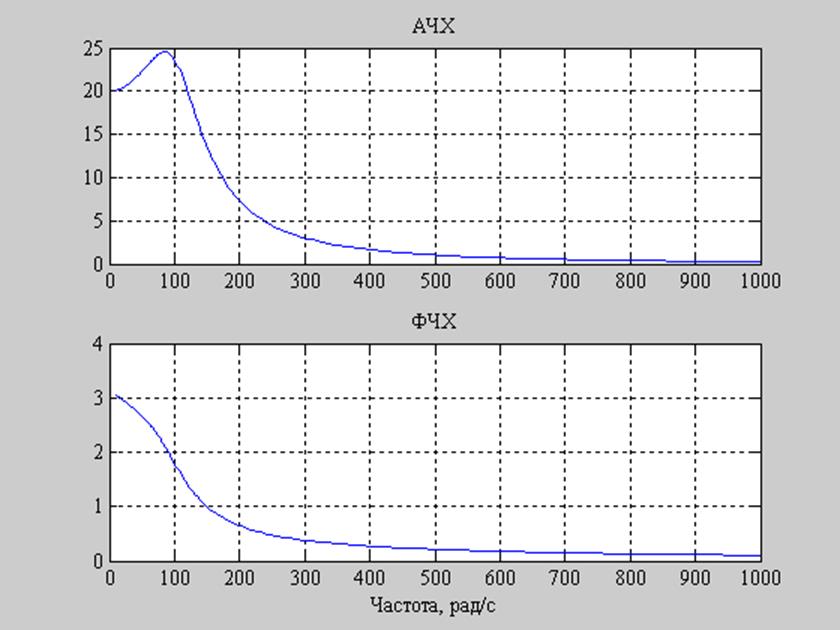
Рис. 13. Графики АЧХ и ФЧХ заданного фильтра при C1=10 мкФ.
С1=50 мкФ
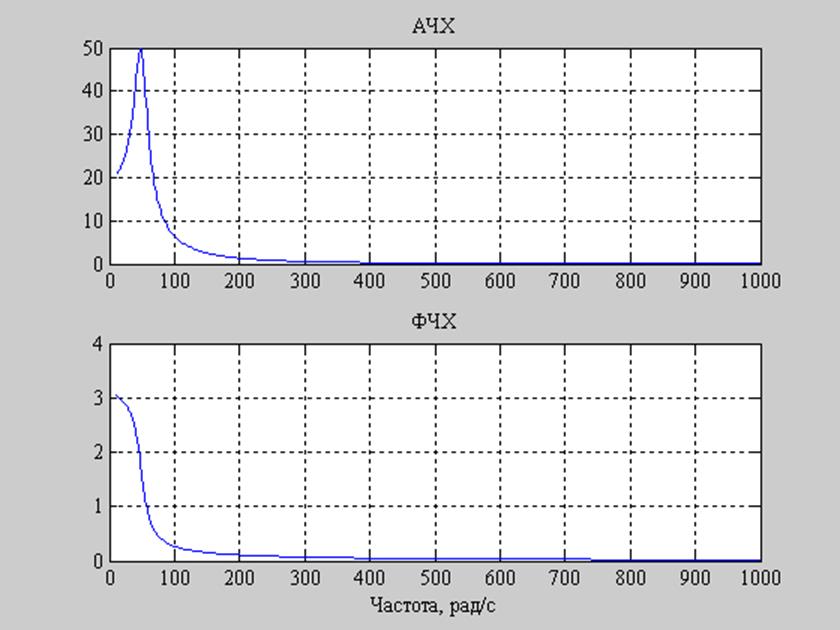
Рис. 14. Графики АЧХ и ФЧХ заданного фильтра при C1=50 мкФ.
Заметим, что при увеличении
емкости конденсатора появляется резонансный эффект. Система обладает
резонансными свойствами с максимальным значением АЧХ на частоте ![]() при С1=10 мкФ,
при С1=10 мкФ, ![]() при С1=50 мкФ.
при С1=50 мкФ.
График ФЧХ быстрее приближается к нулю с увеличением емкости. С ростом емкости С1 полоса пропускания данного фильтра уменьшается.
6. Определение
переходной и импульсной характеристик фильтра.
Во временной области основными характеристиками системы являются её импульсная и переходная характеристики.
Импульсная характеристика системы - это реакция системы на входной сигнал в виде дельта - функции при нулевых начальных условиях.
Переходная характеристика системы – это реакция системы на входной сигнал в виде единичной ступенчатой функции при нулевых начальных условиях.
С помощью следующего script-файла построим графики переходной и импульсной характеристик заданного фильтра, используя функции step() и impulse().
C_num = [0 0 -2.5*10^6];
C_den = [1 1025 1.25*10^5];
step(C_num,C_den);
figure(2)
impulse(C_num,C_den);
Результаты представлены на рис. 8 и рис.9.
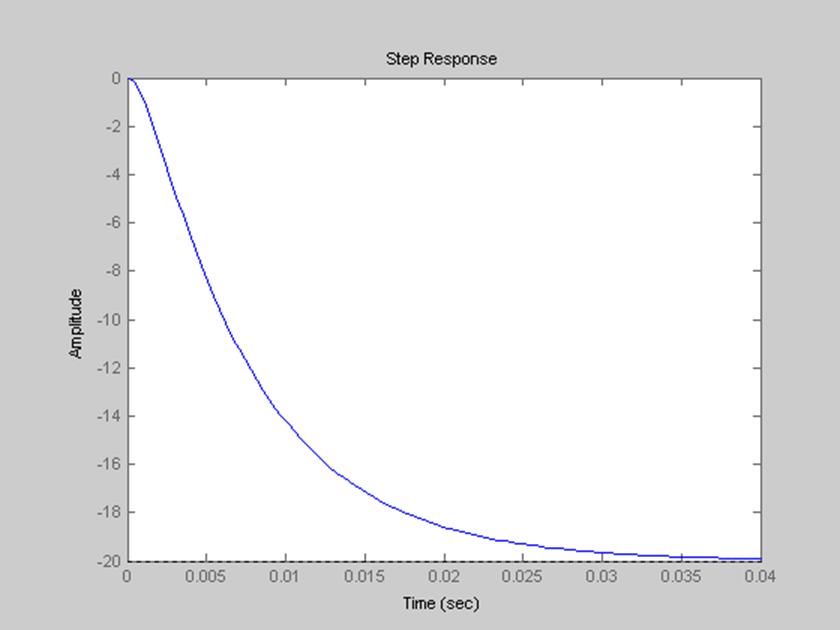
Рис. 8. График переходной характеристики фильтра.
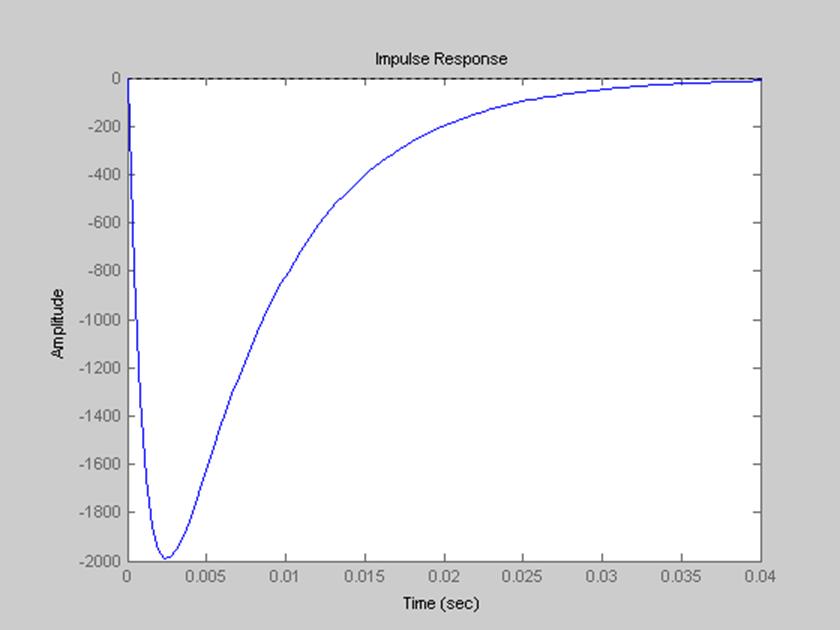
Рис. 9. График импульсной характеристики фильтра.
Импульсная характеристика – реакция системы на входной сигнал в виде δ-функции при нулевых начальных условиях.
Они связаны между собой: 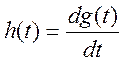
Обратное преобразование Лапласа передаточной
функции системы является импульсной характеристикой данной системы, т.е. ![]() .
.
Найдём импульсную характеристику заданного фильтра аналитически, используя разложение её передаточной функции на простые дроби (выражение (12)).
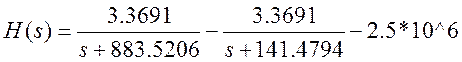
С помощью таблиц преобразования Лапласа находим
![]() и
и 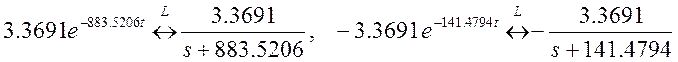 .
.
Преобразование Лапласа обладает
свойством линейности, т.е. если ![]() , то
, то ![]() .
.
Поэтому импульсная характеристика фильтра имеет вид
![]() (16)
(16)
С помощью следующего script-файла построим график импульсной характеристики фильтра по выражению (16).
t = 0: 0.0001: 2.5*10^(-3);
h = 3.3691*exp(-883.5206*t) – 3.3691*exp(-141.479*t) -2.5*10^6;
plot(t, h);
set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)
title('Импульсная характеристика фильтра');
Полученный результат представлен на рис. 10.
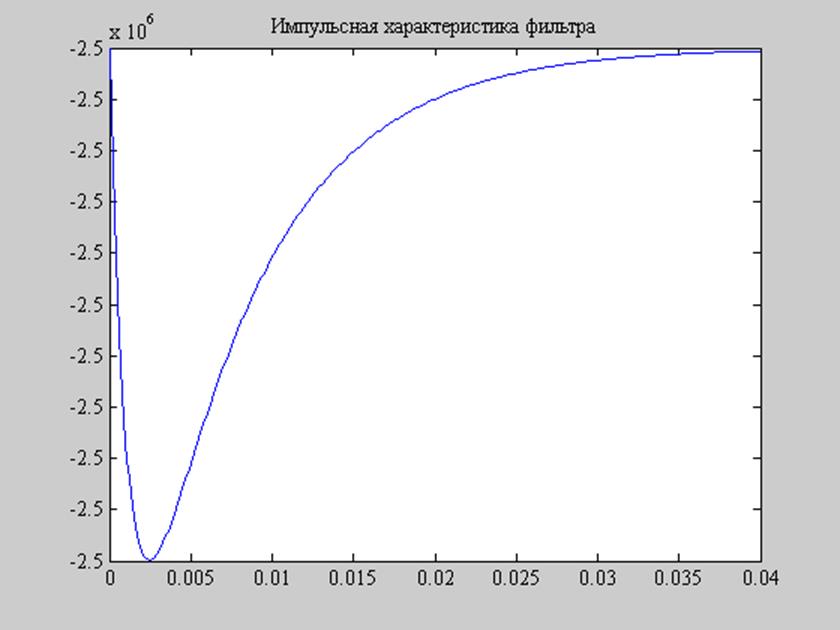
Рис. 10. График импульсной характеристики фильтра по выражению (16).
Видим, что графики рис. 9 и 10 совпадают, значит, импульсную характеристику системы действительно можно получить как обратное преобразование Лапласа переходной функции системы.
7.Построение входного и выходного сигналов
Для гармонического сигнала возьмем частоту 100 Гц (данная частота входит в ПП).
b = [3.37 -3.37 -2.5*10^6];
a = [-883 -141 0];
t = linspace (0 , 0.03, 5000);
f = cos (200*pi*t);
lsim (b, a, f ,t),
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
legend('выходной сигнал','входной сигнал');
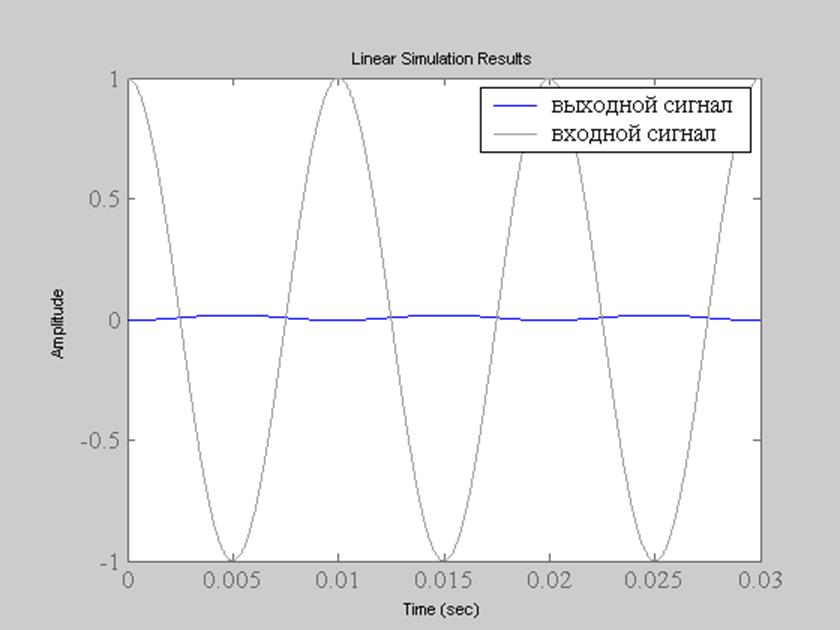
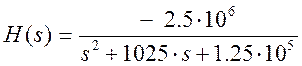
При ![]()
![]()
Отклик системы H(s) на гармонический
вход ![]() есть
есть
![]() .
.
![]()
![]()
![]()
Полученное теоретически значение фазового смещения отрицательное. Это означает, что амплитуда выходного сигнала отстает от входного на некую величину. Но это не наблюдается на графике, т.к. его величина очень мала.
Выводы:
1. Основными характеристиками системы являются её передаточная функция, частотная, импульсная и переходная характеристики.
2. Передаточная функция системы определяется как отношение преобразований Лапласа выходного и входного сигнала.
Передаточная функция связана с
импульсной характеристикой системы через преобразование Лапласа, т.е. ![]() . В п. 6 было показано, что график
импульсной характеристики, полученной с помощью подачи на вход системы
. В п. 6 было показано, что график
импульсной характеристики, полученной с помощью подачи на вход системы
дельта – функции (рис. 9), совпадает с графиком, полученным как преобразование Лапласа импульсной функции (рис. 10).
3. Нули и полюса передаточной функции однозначно её определяют с точностью до коэффициента усиления K, что было показано в п.2 (выражение (11)).
4. Частотная
характеристика системы связана с импульсной характеристикой через
преобразование Фурье, т.е. ![]() . Также данную
характеристику можно получить заменой из передаточной функции системы заменой
. Также данную
характеристику можно получить заменой из передаточной функции системы заменой ![]() .
.
Зная частотную характеристику системы можно построить её АЧХ и ФЧХ. АЧХ характеризует изменение амплитуды гармоники при прохождении её через систему, ФЧХ – изменение фазы гармоники.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.