Изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем. Вариант 6

Министерство Образования и Науки РФ

Новосибирский Государственный Технический Университет

Кафедра Систем Сбора и Обработки Данных

Дисциплина «Теория и Обработка Сигналов»

Лабораторная работа №9

«ЛИНЕЙНЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ»

Вариант № 6

Факультет: АВТ                                                                          Преподаватель:

Группа: АО-61                                                                             Щетинин Ю. И.

Студент: Селиванов Е.

Новосибирск

2009 г.

Цель работы:изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем и приобретение практических навыков  их анализа в среде Matlab.

1.  Дискретизация аналогового фильтра.

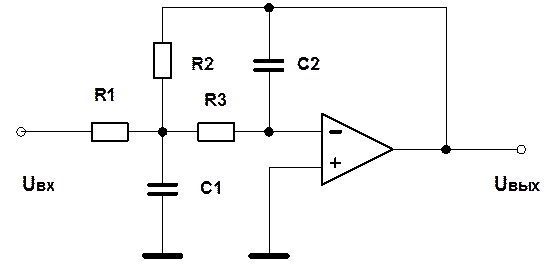
Рис.1. Схема фильтра нижних частот.

В предположении идеального операционного усилителя передаточная функция  фильтра имеет вид

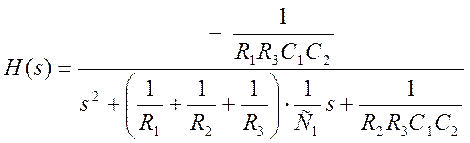
R1=2 кОм,   R2=40 кОм,  R3=2 кОм,  C1=1 мкФ,   C2=0.1 мкФ

Введем обозначения:

b=; ; ; ,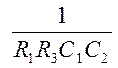

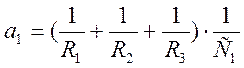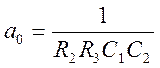b=-2500000;  

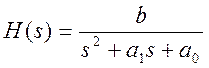
Запишем по виду передаточной функции дифференциальное уравнение, связывающее выходное и входное напряжения фильтра:

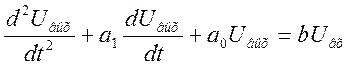
Произведем дискретизацию аналогового фильтра с интервалом отсчетов  Δt.

Для этого заменим производную конечной разностью (интерполяция вперед) вида

,

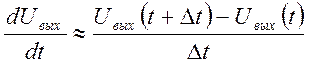где  - величина шага приращения времени (интервал отсчетов, или интервал дискретизации).

Формула для производной второго порядка через конечные разности

.

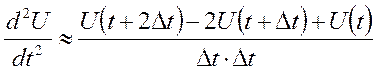При этом уравнение преобразовывается к виду

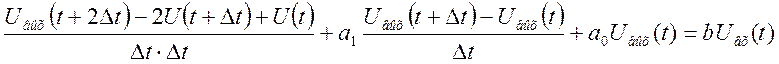
Положим    и  обозначим  , аналогично .

Тогда выражение приобретает вид

Выберем для данного примера значение  F_s = 100000  Гц, что соответствует интервалу (периоду) отсчетов  

Обозначим теперь коэффициенты разностного уравнения, как  и  и  . При этом разностное уравнение можно представить в виде

Для выбранных числовых значений  значения коэффициентов равны ,  ,  и уравнение перепишем в форме

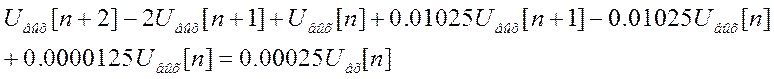
После преобразования

Возьмем  Z- преобразование от левой и правой части уравнения. С учетом теоремы сдвига получим:

Теперь запишем передаточную функцию дискретного фильтра как отношение Z - преобразований выходного и входного сигналов

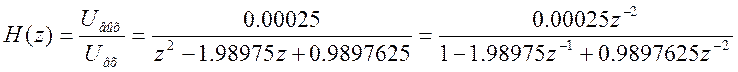
Частотная характеристика  дискретной системы представляет собой передаточную функцию при , т.е.  .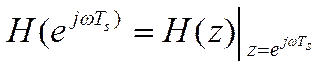

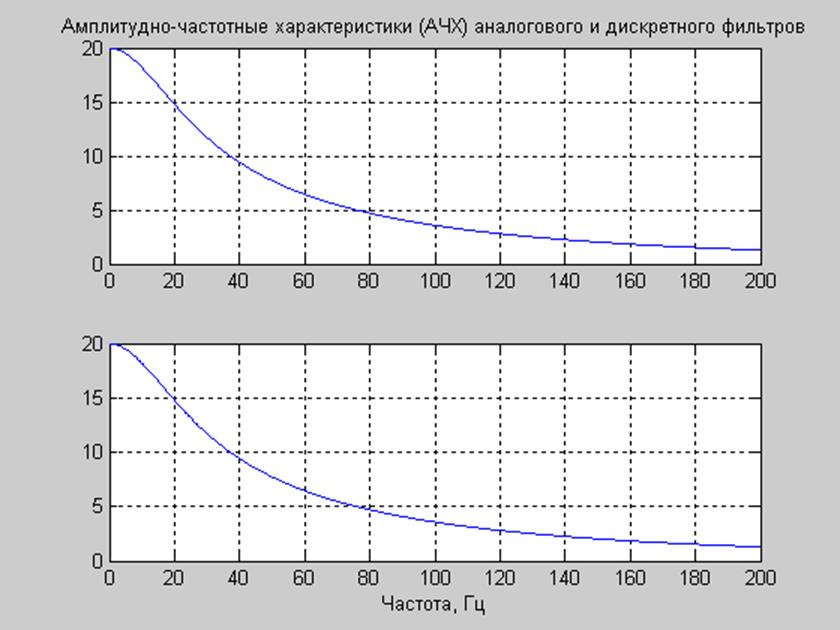
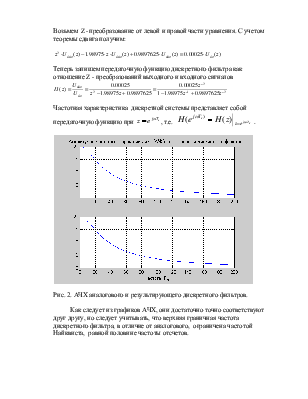
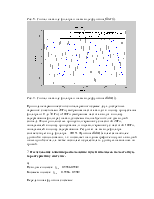
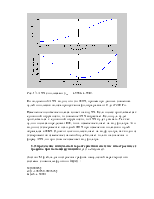
Рис. 2. АЧХ аналогового и результирующего дискретного фильтров.

Как следует из графиков АЧХ, они достаточно точно соответствуют друг другу, но следует учитывать, что верхняя граничная частота  дискретного фильтра, в отличие от аналогового,  ограничена частотой Найквиста,  равной половине частоты отсчетов.

2.  Разложение передаточной функции на простые дроби.

Передаточная функция:

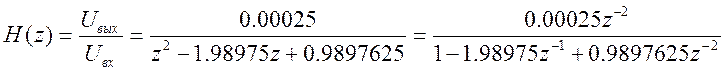
num=[-0.00025];                %коэффициенты числителя

denum=[1 -1.98975 0.9897625];  %коэффициенты знаменателя

[r,p,k]=residuez(num,denum)    %функция разложения на простые дроби

Результат выполнения процедуры:

r =

    0.0336

   -0.0334

p =

    0.9986

    0.9912

k =

     []

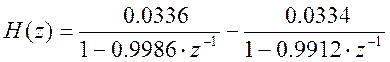
Находим обратное Z-преобразование.

Получаем импульсную характеристику системы.

Построение графика импульсной характеристики:

figure(1);

n=0:1:3000;

h=(0.0336).*((0.9986).^n)+(-0.0334).*((0.9912).^n);

plot(n,h);

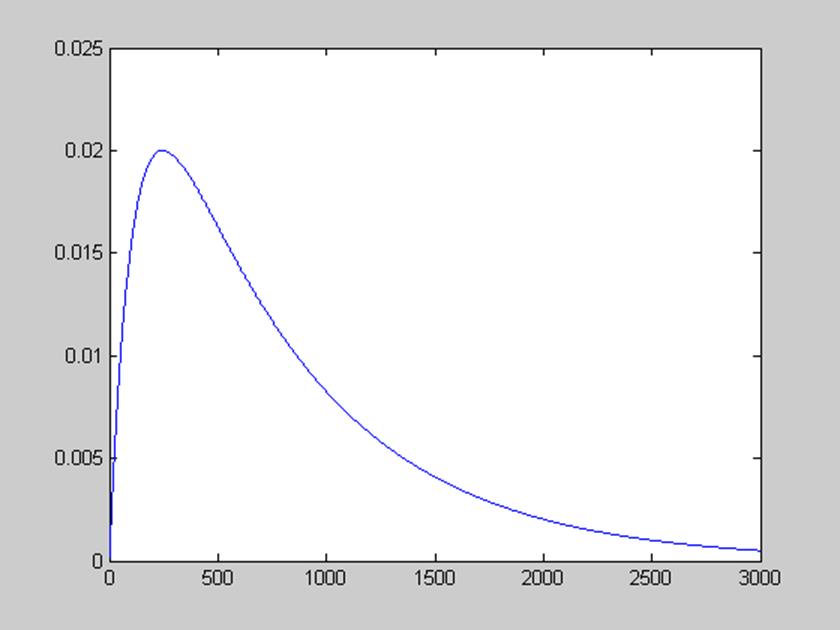
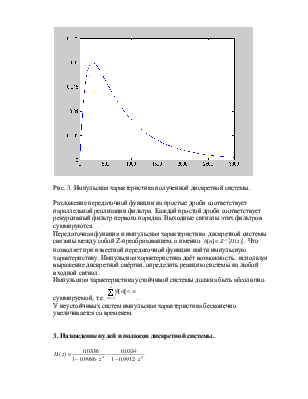
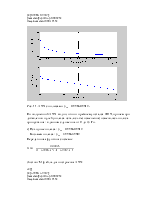
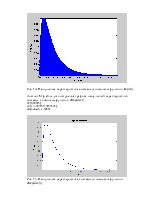
Рис. 3. Импульсная характеристика полученной дискретной системы.

Разложение передаточной функции на простые дроби соответствует параллельной реализации фильтра. Каждой простой дроби соответствует рекурсивный фильтр первого порядка. Выходные сигналы этих фильтров суммируются.

Передаточная функция и импульсная характеристика  дискретной системы связаны между собой Z-преобразованием, а именно  . Что позволяет при известной передаточной функции найти импульсную характеристику. Импульсная характеристика даёт возможность,  используя выражение дискретной свёртки, определить реакцию системы на любой входной сигнал.

Импульсная характеристика устойчивой системы должна быть абсолютно суммируемой, т.е. .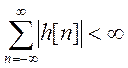

У неустойчивых систем импульсная характеристика бесконечно увеличивается со временем.

3. Нахождение нулей и полюсов дискретной системы.

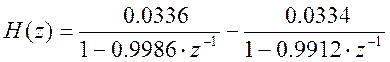
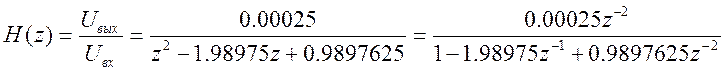
Определение полюсов.

denum=[1 -1.98975 0.9897625];

P=roots(denum);

P =

    0.9986

    0.9912

Нули и полюса однозначно определяют передаточную функцию, а значит и саму систему с точностью до константы - усиления системы.

Построение диаграммы нулей и полюсов фильтра.

a=[0 0 0.00025];

b=[1 -1.98975  0.9897625];

zplane(a,b)

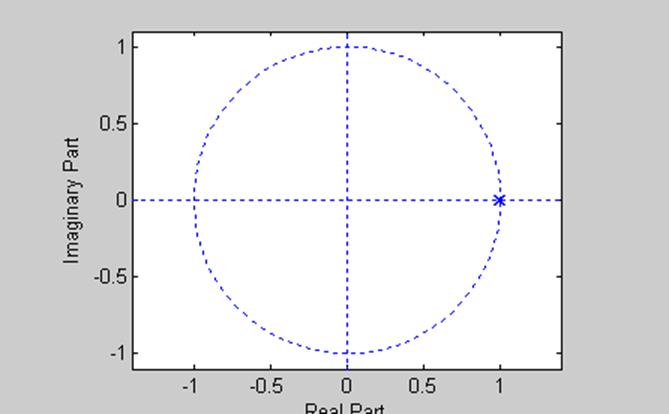
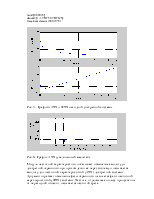
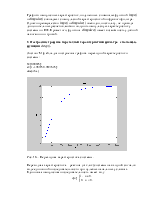
Рис. 4. Диаграмма нулей и полюсов фильтра.

Для устойчивости дискретной системы нужно, чтобы её полюса располагались внутри окружности. Система согласно диаграмме представляет собой устойчивую систему.

4. Определение  частотной характеристики системы.

Листинг M-файла для построения АЧХ и ФЧХ:

num=[0.00025];

denum=[1 -1.98975 0.9897625];

freqz(num,denum,1000,10^5)

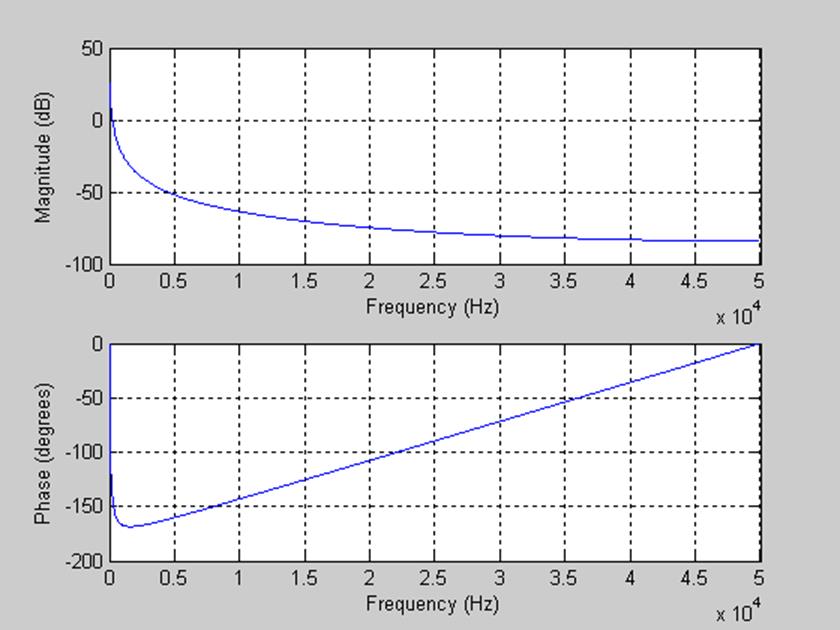
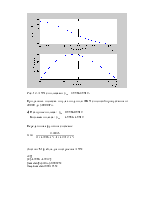
Рис. 5.  Графики АЧХ и ФЧХ исходной дискретной системы.

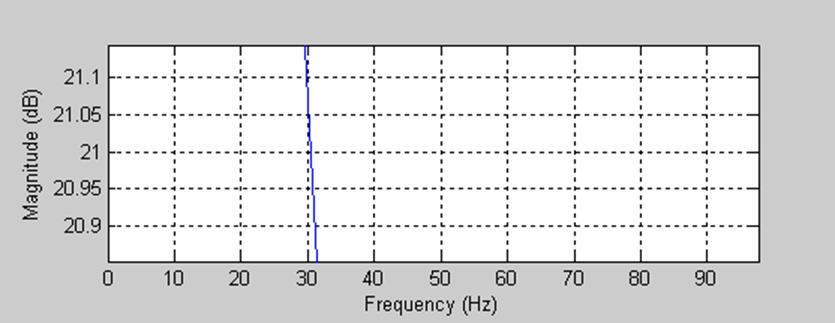
Рис. 6. График АЧХ (увеличенный масштаб).

Модуль частотной характеристики показывает изменение амплитуды дискретной гармоники при прохождении её через систему и называется амплитудно-частотной характеристикой (АЧХ) дискретной системы. Аргумент отражает изменение фазы гармоники и является фазо-частотной характеристикой (ФЧХ) системы. Частота, отделяющая полосу пропускания от переходной области, называется частотой среза.

По Рис. 6. видно, что частота среза по уровню -3дБ примерно равна 20Гц. По Рис. 5. из графика АЧХ видно, что это ФНЧ, значит полоса пропускания от 0 до 20 Гц.

6. Фильтрация гармонических сигналов.

Листинг М-файла для построения графиков гармонических сигналов и графиков сигнала после фильтрации:

n=0:0.1:1000;

Fs=10000;

f1=20;

f2=100;

subplot(3,1,1);

x= cos(2*pi*f1*n/Fs);;

plot(n,x);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

legend('Сигнал с частотой 20 Гц');