Изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем. Вариант 6, страница 2

subplot(3,1,2);

y= cos(2*pi*f2*n/Fs);

plot(n,y);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

legend('Сигнал с частотой 100 Гц');

subplot(3,1,3);

z=x+y;

plot(n,z);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

legend('Сумма двух сигналов');

num=[0.00025];

den=[1 -1.98975 0.9897625];

figure(2);

subplot(211);

plot(n,z);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

legend('Сигнал на входе фильтра');

subplot(212);

F1=filter(num,den,z);

plot(n,F1);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

legend('Сигнал на выходе фильтра (функция filter)');

subplot(212);

figure(3);

dlsim(num,den,z);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

legend(' сигнал на выходе фильтра (функция dlsim)','сигнал на входе фильтра');

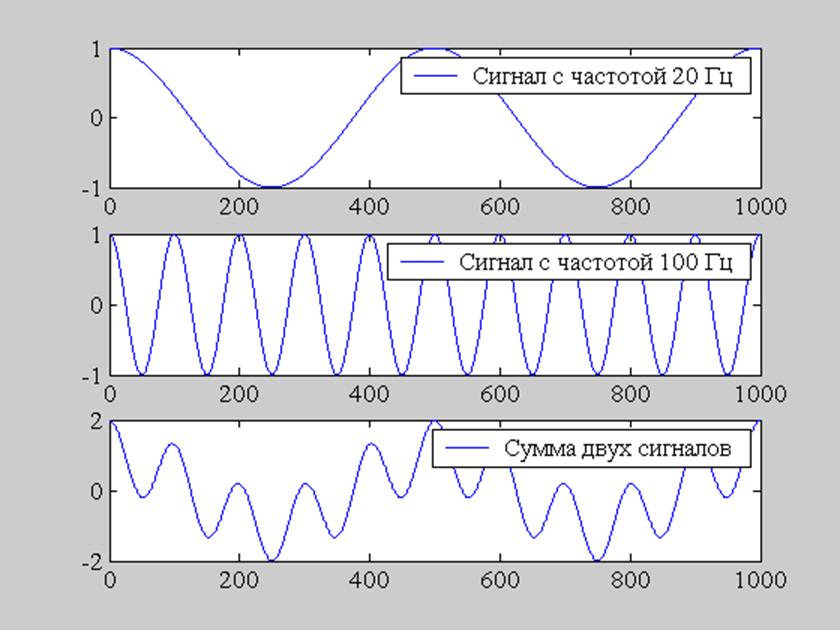
Рис. 7. Графики гармонических сигналов:

а) cos(2*pi*20*n)

б) cos(2*pi*100*n)

в) cos(2*pi*20*n) + cos(2*pi*100*n)

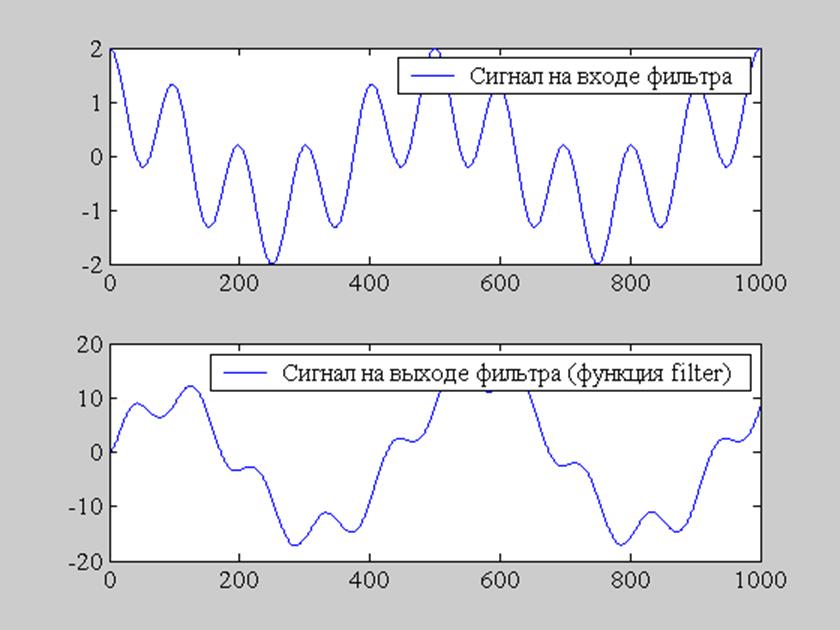
Рис. 8. Сигнал на входе фильтра и на выходе (функция filter()).

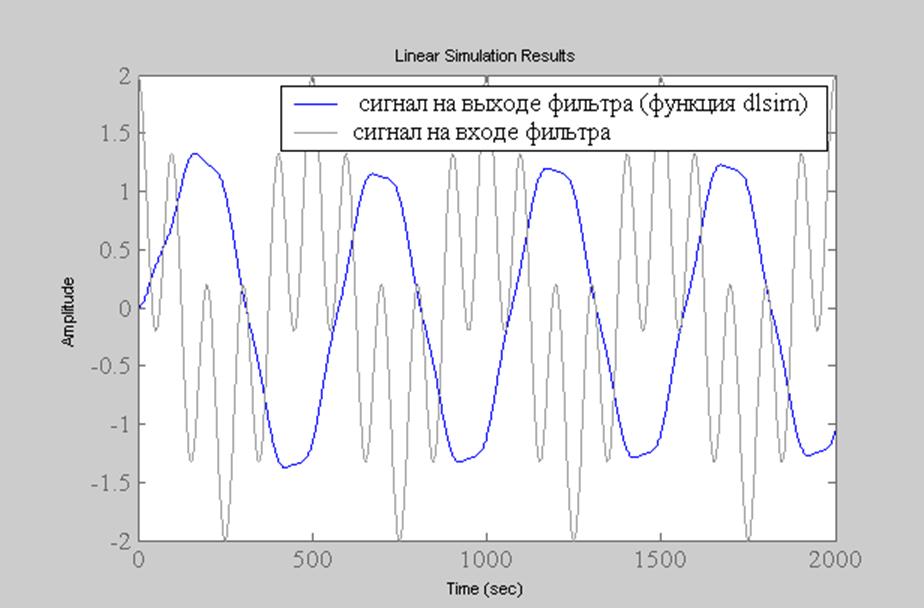
Рис. 9. Сигнал на входе фильтра и на выходе (функция dlsim()).

При подаче гармонического сигнала равного сумме двух дискретных гармоник с частотами 20Гц (выбранная частота входит в полосу пропускания фильтра от 0 до 30 Гц) и 100Гц (выбранная частота входит в полосу задерживания фильтра) на вход системы был найден отклик (выходной сигнал). Фильтр полностью пропустил гармонику с частотой 20Гц, попадающей в полосу пропускания, и подавил гармонику с частотой 100Гц, попадающей в полосу задерживания. Результат на выходе фильтра соответствует виду фильтра – ФНЧ. Функция dlsim() является наиболее удобной в использовании, т.к. позволяет на одном графике получить входной и выходной сигнал, а также позволяет осуществлять удобную навигацию по кривой.

7. Исследование влияния расположения нулей и полюсов на частотную характеристику системы.

a)

Исходные полюса:

Возьмем полюса:

Передаточная функция системы:

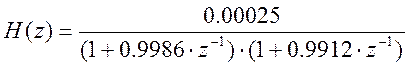
Листинг М-файла для построения АЧХ:

z=[0];

p=[-0.9986; -0.9912];

[num,den]=zp2tf(z,p,0.00025);

freqz(num,den,1000,10^5);

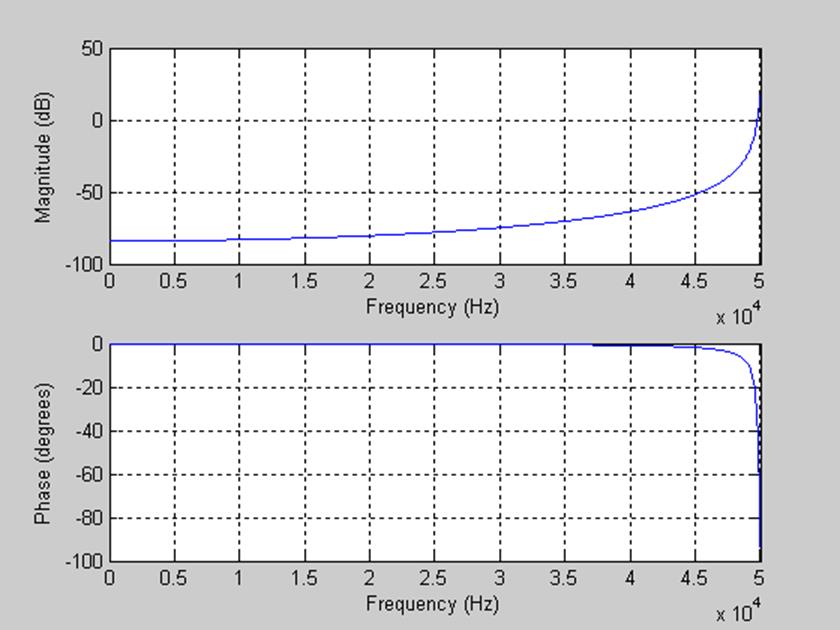
Рис. 10. АЧХ с полюсами

При исходных полюсах был ФНЧ, сменив знак у полюсов, получили ФВЧ с полосой пропускания от 49500 до 50000 Гц, что видно из графика АЧХ.

b) Исходные полюса:

    Возьмем полюса:

Передаточная функция системы:

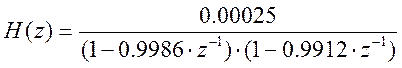
Листинг М-файла для построения АЧХ:

z=[];

p=[0.9986; 0.9912];

[num,den]=zp2tf(z,p,0.00025);

freqz(num,den,1000,10^5);

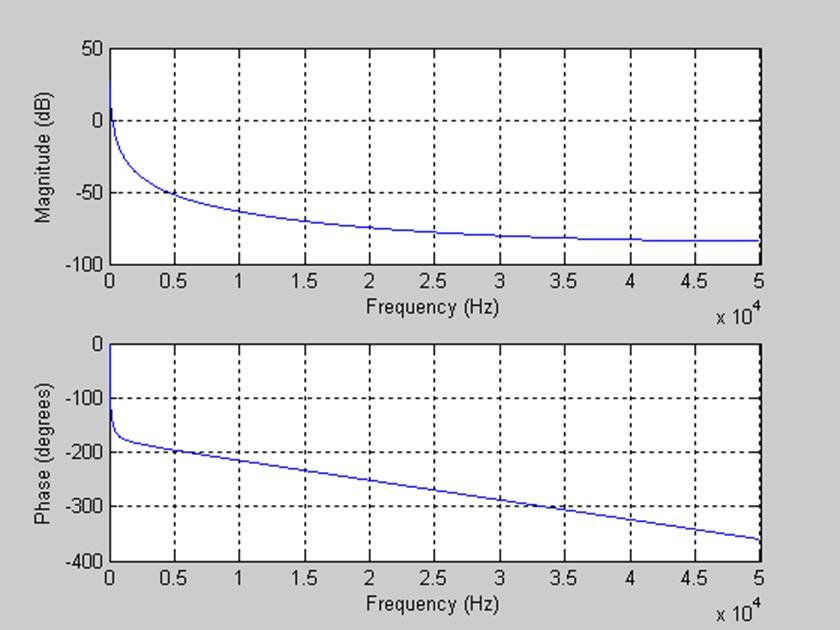
Рис. 11. АЧХ с полюсами .

По полученной АЧХ  видно, что по-прежнему остался ФНЧ, причем при добавлении нулей (полюса остались без изменения) изменилась полоса пропускания: в данном случае она от 0 до 45 Гц.

c) Исходные полюса:

    Возьмем полюса:  

Передаточная функция системы:

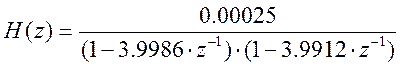
Листинг М-файла для построения АЧХ:

z=[];

p=[3.9986; 3.9912];

[num,den]=zp2tf(z,p,0.00025);

freqz(num,den,1000,10^5);

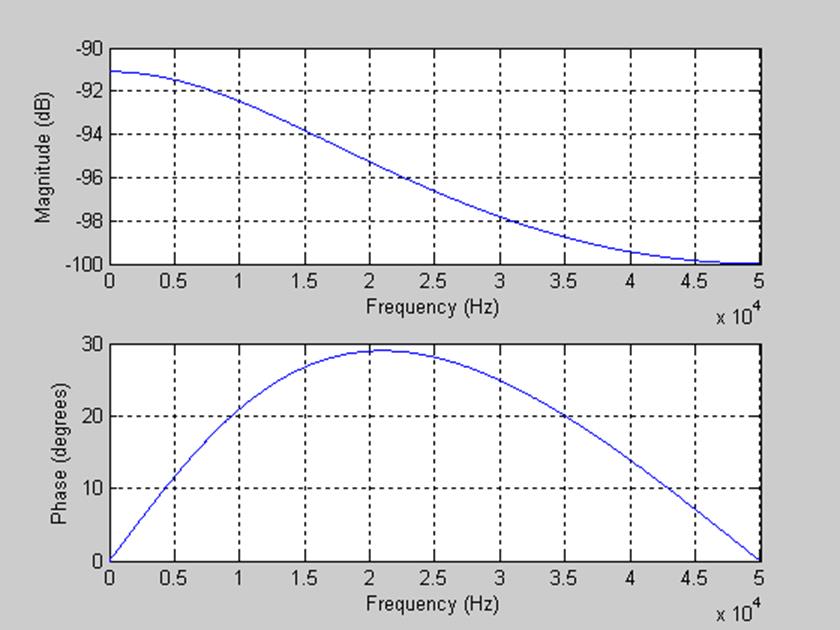
Рис. 12. АЧХ с полюсами .

При данных полюсах и нулях получили ФВЧ с полосой пропускания от 20000 до 50000 Гц.

d) Исходные полюса:

    Возьмем полюса:  

Передаточная функция системы:

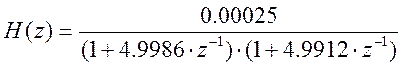
Листинг М-файла для построения АЧХ:

z=[];

p=[-4.9986; -4.9912];

[num,den]=zp2tf(z,p,0.00025);

freqz(num,den,1000,10^5);

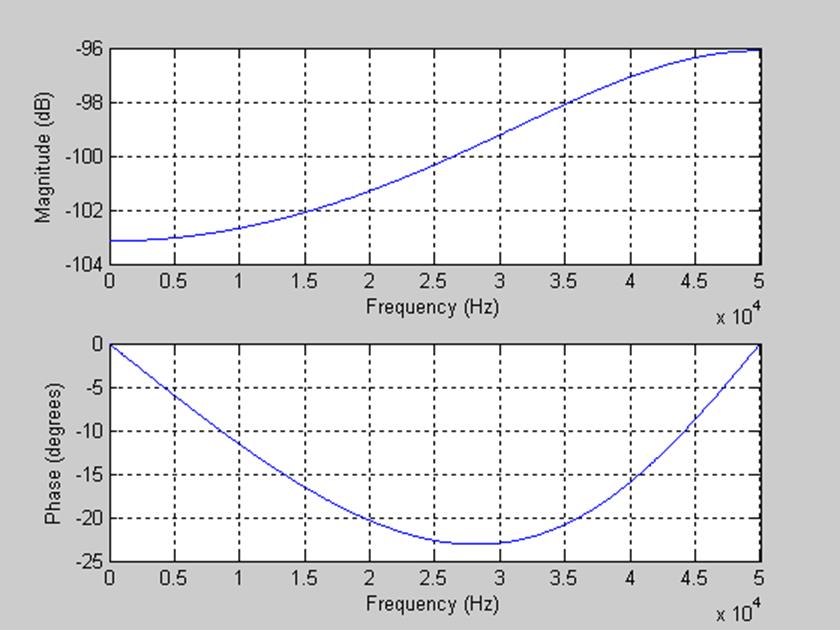
Рис. 13. АЧХ с полюсами  .

По полученной АЧХ  видно, что это ФНЧ, причем при данных значениях нулей и полюсов полоса пропускания фильтра равна от 0 до 27200 Гц.

Изменение положение полюса влияет на вид ЧХ. Если полюс приближается к единичной окружности, то значение АЧХ возрастает. Если нуль будет приближаться  к единичной окружности, то АЧХ будет убывать. Так как нули и полюса определяют ПФ, то их изменение влияет на вид фильтра. Это видно из эксперимента: исходный ФНЧ при изменении полюсов и нулей обращался в ФВЧ. Однако только полюс влияет на вид фильтра, как видно из экспериментов изменение значений нулей влияет только на значения и форму АЧХ, но при этом не изменяет вид фильтра.

8. Определение импульсной характеристики системы и построение её графика при помощи функций impz() и dimpulse().

Листинг М-файла для построения графика импульсной характеристики системы с помощью функции impz()  :

b=[0.00025];

a=[1 -1.98975 0.9897625];

impz(b, a, 5000)

Рис. 14. Импульсная характеристика системы (с помощью функции impz()).

Листинг М-файла для построения графика импульсной характеристики системы с помощью функции dimpulse() :

b=[0.00025];

a=[1 -1.98975 0.9897625];

dimpulse(b, a, 5000)

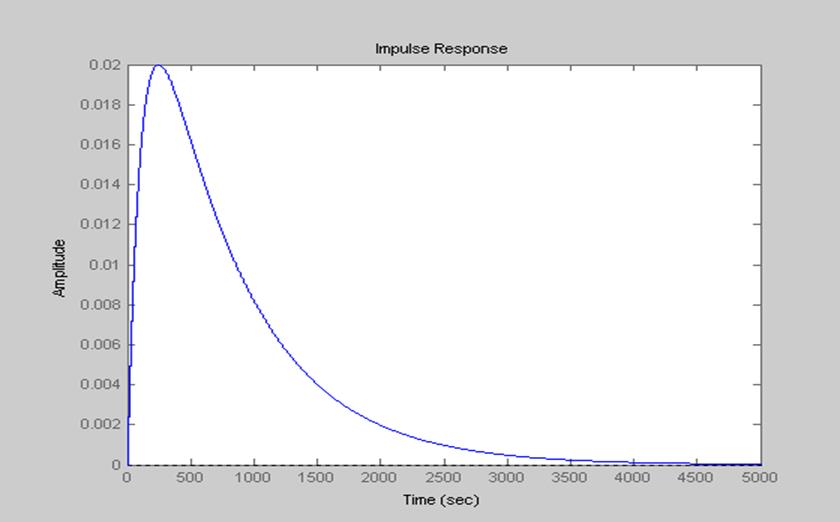
Рис. 15. Импульсная характеристика системы (с помощью функции dimpulse()).

Графики импульсных характеристик, полученных с помощью функций impz() и dimpulse()совпадают с импульсной характеристикой цифрового фильтра. Однако преимущество impz() и dimpulse() очевидно, поскольку, не проводя дополнительных расчетов, можно получить импульсную характеристику системы по ПФ. Кроме того, функция  dimpulse() имеет возможность удобной навигации по кривой.

9. Построение графика переходной характеристики фильтра  с помощью функции dstep().

Листинг М-файла для построения графика переходной характеристики системы:

b=[0.00025];

a=[1 -1.98975 0.9897625];

dstep(b, a)

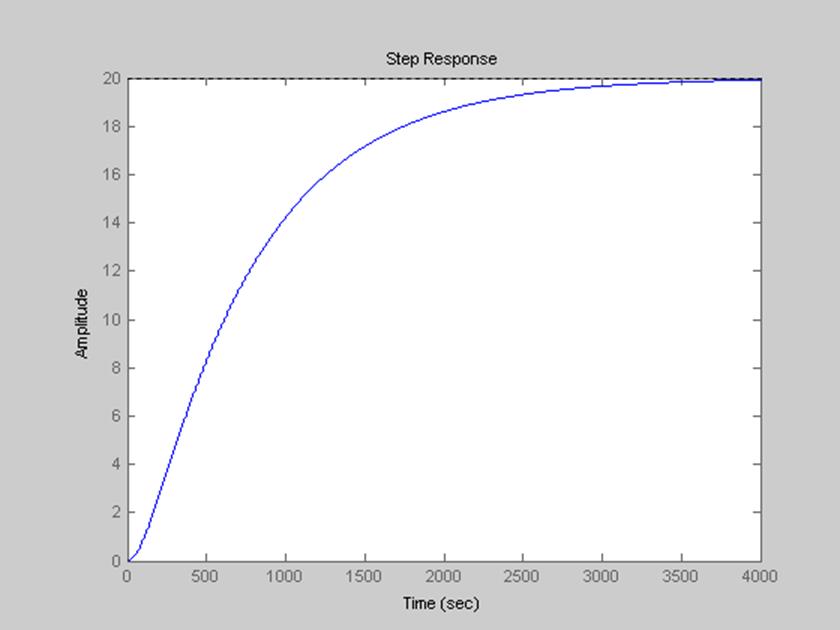
Рис. 16. . Переходная характеристика системы.

Переходная характеристика – реакция (отклик) системы на входной сигнал в виде единичной последовательности при нулевых начальных условиях.

Единичная импульсная последовательность имеет вид:

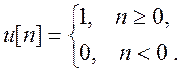
Через единичный импульс: 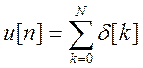. Если подать на вход 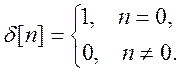, то на выходе получается импульсная характеристика , если учесть линейность системы, то если на вход подаётся сигнал вида 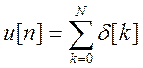, то на выходе будет 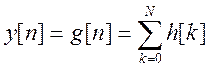. Т.е. переходная характеристика есть сумма импульсных характеристик. Учитывая линейность системы, получаем связь импульсной и переходной характеристики:

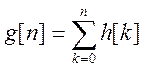, где g[n]- переходная характеристика.