Дискретное преобразование Фурье и спектральный анализ сигналов: Методические рекомендации по выполнению лабораторной работы

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

Дисциплина  «Теория  и  обработка  сигналов»,     5 - й семестр

ЛАБОРАТОРНАЯ  РАБОТА  № 4

ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ

И СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ

Цель работы:изучение дискретного преобразования Фурье  (ДПФ) и его вычисления, алгоритма быстрого преобразования Фурье с прореживанием по времени,  использования ДПФ для  спектрального анализа сигналов.

Задание и порядок выполнения работы.

1.  Ознакомьтесь с дискретным преобразованием  Фурье  (ДПФ), его свойствами и алгоритмом быстрого преобразования Фурье (БПФ)  по  учебной литературе, например,  [1] стр. 87-100 или [2]  стр. 249-260.

2.  Используя  функцию dftsum() для вычисления ДПФ по выражению 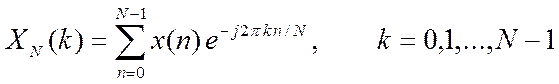(1)

      ,          (1)
составленную в лабораторной работе № 3, вычислите ДПФ следующих сигналов

          а)    для  N = 10.

          а)  x(n) = 1 для N = 10,

          б)  x(n) = cos(2πn/10) для  N = 10.

Постройте графики сигналов и их амплитудных спектров для каждого случая.

Объясните характер спектров.

3.  Напишите Matlab-функцию для вычисления обратного (инверсного) ДПФ с форматом   x = idftsum(X).  Формула вычисления этого преобразования

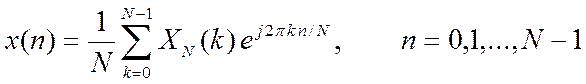                    ,                    (2)

где X – N-точечный вектор ДПФ,   x – вектор сигнала во временной области.

Примените написанную Вами функцию idftsum(X) для вычисления обратного ДПФ  вышеприведенных сигналов. Сопоставьте графики исходных сигналов и результаты вычисления с помощью idftsum(X).

4.  Вычислите с помощью функции dftsum(x)  ДПФ случайной последовательности  длиной 1021  точек.  Для генерирования   последовательности используйте функцию randn(). С помощью встроенной  в Matlab функции  cputime  (или процедуры tic...toc) определите время вычисления функции  dftsum(x).   Соответствующий пример представлен в Приложении 1.

5.  Вычислите ДПФ случайной последовательности длиной 1021 точек с помощью встроенной в Matlab функции fft(). Определите (функция cputime) время вычисления  ДПФ и сопоставьте его с  временем вычисления функции dftsum().
          Обратите внимание, что в функции fft() используется алгоритм быстрого преобразования Фурье (БПФ, англ. FFT), который имеет наивысшую скорость, когда длина последовательности данных является степенью числа 2, в противном случае используется алгоритм БПФ, обладающий меньшей производительностью. Число 1021  является простым, не разлагается на множители, поэтому время вычисления БПФ для данного случая является относительно большим, хотя и значительно меньшим, чем с помощью функции dftsum().
         Представьте в отчете в краткой форме описание основной идеи алгоритма БПФ с прореживанием по времени.

6.  Определите ближайшее сверху к значению 1021 число, являющееся степенью 2. Найдите время вычисления ДПФ для последовательности такой длины с помощью функций dftsum() и fft(). При вычислении с помощью fft() организуйте цикл из 1000 вычислений и разделите общее время вычисления цикла на 1000, поскольку единичное вычисление ДПФ в этом случае получается очень быстрым и не может быть определено с достаточной точностью.

7.  Одной из областей, которая основана на использовании ДПФ, является спектральный анализ, задача которого заключается в определении частотного спектра измеряемого сигнала (процесса).

          Ознакомьтесь и выполните процедуру  из Приложения 2. Здесь  рассматривается  простая задача определения частотного спектра сигнала, состоящего из суммы двух гармоник и случайного шума. Для определения спектра используется процедура fft() Matlab. При этом получается обычный ДПФ - спектр с индексами частот .  Для перегруппировки выходного массива преобразования Фурье применяется функция fftshift().
          Объясните характер полученного результата. Почему  использование частотной области позволяет определить гармонические составляющие сигнала, а  во временной области даже обнаружить гармоники невозможно?
8.    Важной характеристикой спектрального анализа является его «разрешающая способность» или  «частотное разрешение»,  которая определяет возможность выделения соседних частот спектра сигнала как отдельных линий.
          В процедуре спектрального анализа на основе ДПФ частотное разрешение , т.е.  расстояние между соседними  разрешаемыми частотами анализа,   определяется по выражению
                             ,                                                                (3)

где   - частота дискретизации,

        Ts - интервал дискретизации,

        N– размер ДПФ,

         T – длительность анализируемого  сигнала (длина реализации).

Составьте  и выполните программу, которая

а) формирует сигнал как сумму гармоник с частотами  f₁= 22 Гц, f₂= 34 Гц, амплитудами А₁ = 0,5 ,  А₂ = 1,  частотой дискретизации   Fs = 200 Гц,  числом точек сигнала M = 16;

б)  вычисляет спектр Фурье сигнала с помощью N – точечного ДПФ;

г)  строит в одном окне масштабированные графики сигнала и его амплитудного спектра.

        Выполните программу для  N = 16,  N = 64  и  N = 128 при длине сигнала

М = 16 отсчетов.  Сделайте вывод о влиянии размера ДПФ N  на частотное разрешение.
Примечание: при  N> M при   вычислении   процедура  fft()дополняет  сигнал нулевыми значениями (zeropadding)  до значения  N. При этом естественно использовать N = 2^q.

9.    Обратите внимание, что спектры  гармоник в результатах  анализа из предыдущего пункта  состоят из многих линий.  Эта особенность поведения спектра носит название «утечки» или «растекания ( leakage)»   мощности  сигнала на соседние линии спектра.   
          Объяснение  растекания спектра: ограничение сигнала во времени (усечение) можно трактовать,  как умножение неограниченного по длительности сигнала на прямоугольное окно единичной высоты  длительностью Т.   В частотной области  такому умножению  соответствует свертка исходного спектра со спектром прямоугольного окна.  Спектр прямоугольного окна (импульса)  кроме основного лепестка имеет достаточно большие боковые лепестки.   Боковые лепестки спектра прямоугольного окна, свертываясь с истинными  спектральными составляющими сигнала, добавляют ложную мощность на соседние частоты (более подробно см. Л.[1], стр. 59-60).

 Для уменьшения влияния растекания спектра («утечки энергии») в спектральном анализе используется оконная обработка анализируемого сигнала, которая заключается в умножении анализируемого сигнала на ту или иную оконную функцию со сглаживающими свойствами. Преобразование Фурье оконных функций имеют значительно  меньшие уровни боковых лепестков по сравнению с их уровнями у спектра прямоугольного окна.  В результате умножение сигнала конечной длительности на оконную функцию  (оконная обработка)  уменьшает эффект растекания спектра.                        

Matlab имеет более десятка встроенных функций для генерирования  наиболее  распространенных окон. Функцию нужного окна можно, в частности, вычислить  и построить её  график с помощью процедуры  window().     См. справочные сведения по процедуре.

     Измените программу вычисления и вывода спектра сигнала из суммы двух гармоник (п. 8), дополнив её обработкой сигнала оконной функцией Хэмминга (hamming())  в виде     ’. Выполните программу для М = 16 и размера ДПФ  N = 64.   При этом должно быть предусмотрено построение графиков исходного сигнала и  сигнала, взвешенного окном,  и их амплитудных спектров. 

        Пронаблюдайте и прокомментируйте результаты. Сравните с результатом из предыдущего пункта.  Полезным может быть  также выполнение программы с другими оконными функциями.   

        В заключение этой части работы  выполните программу при длине сигнала M =256, длине БПФ  N=512, прокомментируйте полученный результат.