Информатика и выч. техника \ Теория и обработка сигналов

Дискретное преобразование Фурье и спектральный анализ сигналов: Методические рекомендации по выполнению лабораторной работы, страница 2

10.   Используя    процедуру из Приложения 3 как прототип, составьте программу для вычисления и вывода графиков во временной и частотной области фрагмента речевого сигнала (файл «MySpeech.wav»  из папки «Лабораторные работы»).   Для считывания wav-файла используйте  команду с форматом  y=wavread(‘filename’),  для прослушивания  - команду sound(y, Fs), для определения  числа отсчетов на один канал в файле – команду  N = length(y),  для

определения  частоты дискретизации  Fs при записи звукового файла  -  команду   [y,Fs]=wavread(' MySpeech ', 1).

          Графики результатов этой части работы должны содержать вид сигнала во временной области и его амплитудный спектр. В программе используются данные о длине (числе элементов)  речевого сигнала и частоте дискретизации. Поскольку графики содержат большое число отсчетов, полезно увеличить и рассмотреть отдельные характерные фрагменты  графиков.

          В заключение добавьте в программу команды вида  figure(2),  specgram(y(:,1),[],Fs)   и постройте  спектрограмму звукового сигнала.  Команда specgram()  без выходных параметров  строит графическое изображение спектрограммы в координатах  «время – частота». При этом значения амплитудного спектра отображаются с помощью цвета. Чем больше амплитуда, тем более ярким оранжевым цветом она отображается.  Чем меньше амплитуда спектральной составляющей, тем более темноголубой  у нее цвет. Проанализируйте полученную спектрограмму и сопоставьте её с данными графиков сигнала и его амплитудного спектра, построенными  ранее.

          Указание. Вы можете записать собственный  wav – файл с помощью средств Windows или  командой  wavrecord()  Matlab  и использовать его фрагмент для анализа вместо файла «MySpeech», тем самым изучив особенности спектра собственного голоса.

11.  Сделайте необходимые пояснения, комментарии и выводы к отчету. Окончательно оформите отчет по лабораторной работе.    В отчете должны быть представлены

§  титульный лист,

§  название и цель работы,

§  формулировки пунктов работы, команды и  .m – файлы, графики,
          комментарии, выводы.

Проверьте освоение материала по контрольным вопросам и упражнениям.
Защитите лабораторную работу.



ЛИТЕРАТУРА.

1.  Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. Пособие.- Новосибирск. Изд-во НГТУ,  1998 - ч.1, стр. 87 - 100.

2.  Сергиенко А.Б.  Цифровая обработка сигналов. - СПб.: Питер, 2003,
стр. 249 – 260.

3.  Щетинин Ю.И. Теория и обработка сигналов. Методические указания к решению задач и упражнений . Новосибирск: Изд-во НГТУ, 2007.

4.  Сато Ю. Обработка сигналов. Первое знакомство. / Пер. с яп.; под ред. Ёсифуми Амэмия. – М.: Издательский дом «Додэка - ХХI», 2002,

     стр 113 – 138.

Web – ресурсы

1.  http://tiger.cs.nstu.ru/tos/nperiodic/start.html

2.  http://www.mathworks.com/access/helpdesk/help/toolbox/signal/signal.shtml

Контрольные вопросы и упражнения.

1.  Запишите и объясните выражение дискретного преобразования Фурье (ДПФ).

Сигнал х[n] конечной длины 0<=n<=N-1,только в N-точках частоты равны

wk=2*pi*k/N,

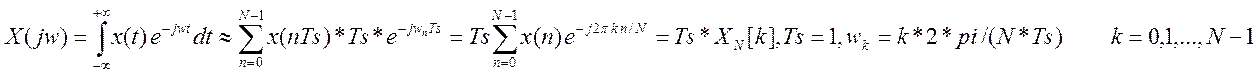Ts=1 при наиболее точном приближении.

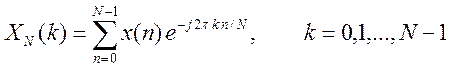
2.  Найдите ДПФ сигнала  x[k] = {-1,  0,  -1,  0}. Изобразите спектр амплитуд и спектр фаз.

Решение.

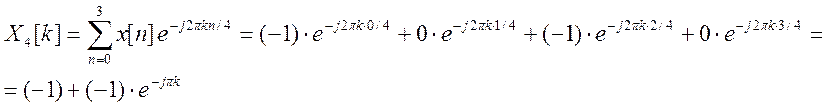
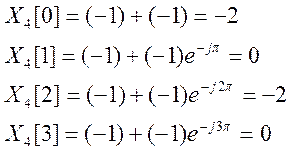
Второй способ решения с использованием свойств ДПФ

Исходный сигнал можно представить в виде суммы сигналов x1[n]  и  x2[n]

 

  1.  
  2.  

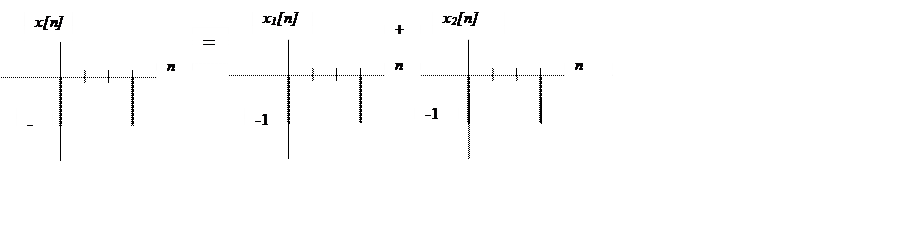ДПФ сигнала  x1[n]  ,

По свойству временного сдвига ДПФ сигнала x2[n]

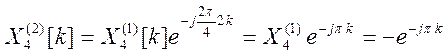
По свойству линейности  ДПФ  ,    отсюда

3.  Определите ДПФ сигнала
                                          

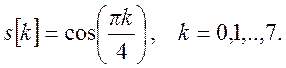
4.  Определите сигнал, спектр (ДПФ) которого имеет вид  
X[n]={1, 1+i, 1, 1-i}.

5.  Сигнал x[k]  имеет ДПФ  X[n]={16,  0,  -3,  5,  16,  0,  -3,  5}.  Какой вид имеет ДПФ сигнала x[k-4]?

6.  Известна часть коэффициентов ДПФ X[n] = {1, 1+i, 1+i2, 1-i3,  -2,  *,  *,  *} некоторого сигнала. Полагая, что N=8,   восстановите недостающие значения ДПФ с помощью свойства симметрии.XN [-k]=XN[N-k]

7.  Сформулируйте и докажите свойство свертки ДПФ.

8.  Используя теорему Парсеваля для ДПФ, найдите среднюю мощность сигнала  . Сопоставьте результаты вычисления во временной и частотной области.

9.  Что такое быстрое преобразование Фурье?  Кратко объясните сущность алгоритма БПФ с прореживанием по времени.

Берем ряд значений x[n] делим на две равные части,записываем преобразование фурье сигнала,как сумму двух сумм этих частей  с числом коэффициентов в 2 раза меньше,чем число отсчетов сигнала.

10.     Объясните синтаксис функции fft() вычисления ДПФ.

11.     Проведите сравнительный анализ быстродействия обычного и быстрого (БПФ) преобразований Фурье.обычное преобразование требует N^2 умножений и N(N-1) сложений, быстрое преобразование при представлении N=2^m,требует приблизительно N*log2(N) умножений.

12.     В среде Matlab определите 128-точечное ДПФ сигнала

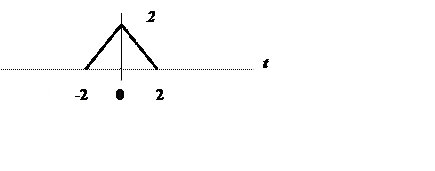
Постройте график амплитудного спектра сигнала.

13.  В чем заключается содержание  задачи спектрального анализа сигнала?

14.  Как используется БПФ в спектральном анализе сигналов?

15.  Что такое частотное разрешение спектрального анализа? От каких факторов оно зависит?  Как можно увеличить частотное разрешение?

Fk=k*Fs/N=k*1/(T*N), дельта(w)=2*pi/N-частотное разрешение в области дискретной частоты wd=w/Fs.

При N-точечном ДПФ частотные компоненты с полосой <дельта(w) не разрешимы,не различимы при анализе с (.)N.Lkz увеличения разрешения следует увеличить число(.)ДПФ.

16.  Что такое «утечка» или «растекание» спектра в спектральном анализе?

17.  Для чего используется оконная обработка исследуемого процесса в спектральном анализе?

18.  Как можно определить спектр речевого сигнала?

Приложение 1. Пример определения времени вычисления ДПФ с помощью        функции dftsum()

% Файл – сценарий

t=0:0.001:0.502;

% Формирование случайной последовательности

x=2*randn(size(t));

t1=cputime;   %  Начало времени вычисления ДПФ

y=dftsum(x);  % Вычисление  ДПФ

t2=cputime - t1 % Конец времени вычисления

% Построение графиков во временной и частотной области

subplot(211), plot(t,x)

subplot(212), plot(abs(y))

Приложение 2.

% Пример задачи спектрального анализа

Fs=64;   % Частота отсчетов

f1=10;    % частоты  гармоник

f2=25;

N=128;   % число отсчетов сигнала

n=0:(N-1);

t=0:1/Fs:(N-1)/Fs;  % вектор времени

% генерирование сигнала для анализа

x=cos(2*pi*f1*t)+0.5*cos(2*pi*f2*t)+randn(1,length(t));

subplot(311), plot(t,x), grid   % график сигнала

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title(‘Сигнал во временной области’)

k=0:(N-1);

f=k*Fs/N;   % частотная шкала

X=fft(x);    % вычисление ДПФ

subplot(312), plot(f,abs(X)/Fs), grid

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Амплитудный cпектр, положительные частоты')

% Построение спектра для положительных и отрицательных частот

k1=-N/2:(N/2-1);

f1=k1*Fs/N;

subplot(313), plot(f1,fftshift((abs(X))/Fs)), grid

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Амплитудный cпектр')

xlabel('Частота,  Гц')

Приложение 3.

% Процедура для построения сигнала и его спектра

N=64;

n=-N/2:N/2-1;

Fs=128;    % Частота отсчетов

f1=10;     % Частота гармоники

n1=n+N/2;

y=cos(2*pi*f1*n1/Fs); % сигнал

Y=fft(y);  % Вычисление  ДПФ 

Yp=fftshift(Y);  % Сдвиг ДПФ

f=n*Fs/N;   % Частотная шкала

figure(1), subplot(211), plot(n1/Fs,y,'ko-')

grid

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

xlabel('Время, с')

title(' Сигнал ')

subplot(212), stem(f,abs(Yp)/N)

grid

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

xlabel('Частота, Гц')

title('Амплитудный спектр сигнала')

Составил  доц.  Щетинин  Ю.И.

Скачать файл